Файл: Сборник задач по высшей математике. РостовнаДону 2008г. 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 69
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
136)
137)
138)
139)
140)
141)
142)
143)
144)
145)
146)
147)
148)
149)
150)
В задачах 151-166 найти область сходимости заданных функциональных рядов:
151)
152)
153)
154)
155)
156)
157)
158)
159)
160)
161)
162)
163)
164)
165)
166)
Используя интегрирование и дифференцирование степенных рядов, найти сумму заданных рядов:
167)
168)
169)
170)
§4 Ряды Тейлора.
Определение. Рядом Тейлора для функции
в окрестности точки 
называется степенной ряд. 
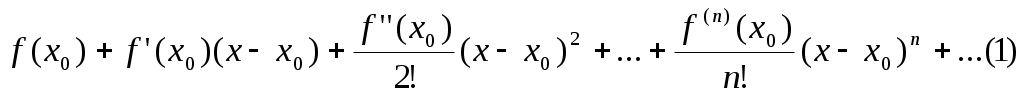
Обозначим
многочлен 
- ой степени, представляющий - ую частичную сумму ряда Тейлора:
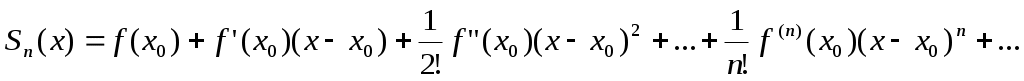
Ряд Тейлора функции
сходится к самой этой функции, если 
. Остаточным членом ряда Тейлора называется разность 
Если ряд Тейлора в области сходимости имеет своей суммой
, то остаточный член этого ряда при 
стремится к нулю и обратно.Величина
дает как раз ту ошибку, которую мы делаем, заменяя функцию многочленом 
.Для выяснения, стремится ли
к нулю при или нет, полезна следующая теорема, устанавливающая структуру остаточного члена: Теорема: Если функция
во всех точках некоторого интервала, содержащего точку , имеет 
ую производную
, то остаточный член 
для любой точки этого интервала имеет вид: 
, где 
можно записать и так:
, где 
Это остаточный член в форме Лагранжа.
Для разложения данной функции в ряд Тейлора нужно
1) написать ряд Тейлора для данной функции, т.е. вычислить значения этой функции и ее производных при
и подставить их в общее выражение ряда Тейлора;2) Исследовать остаточный член
формы Лагранжа для данной функции и определить совокупность значений 
, при которых полученный ряд сходится к данной функции (т.е. при которых 
).Пример. Разложить в ряд Тейлора функции:
1)
при 
; 2) 
при 
Решение:
1) Вычисляем значения данной функции и ее производных при
:
___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___
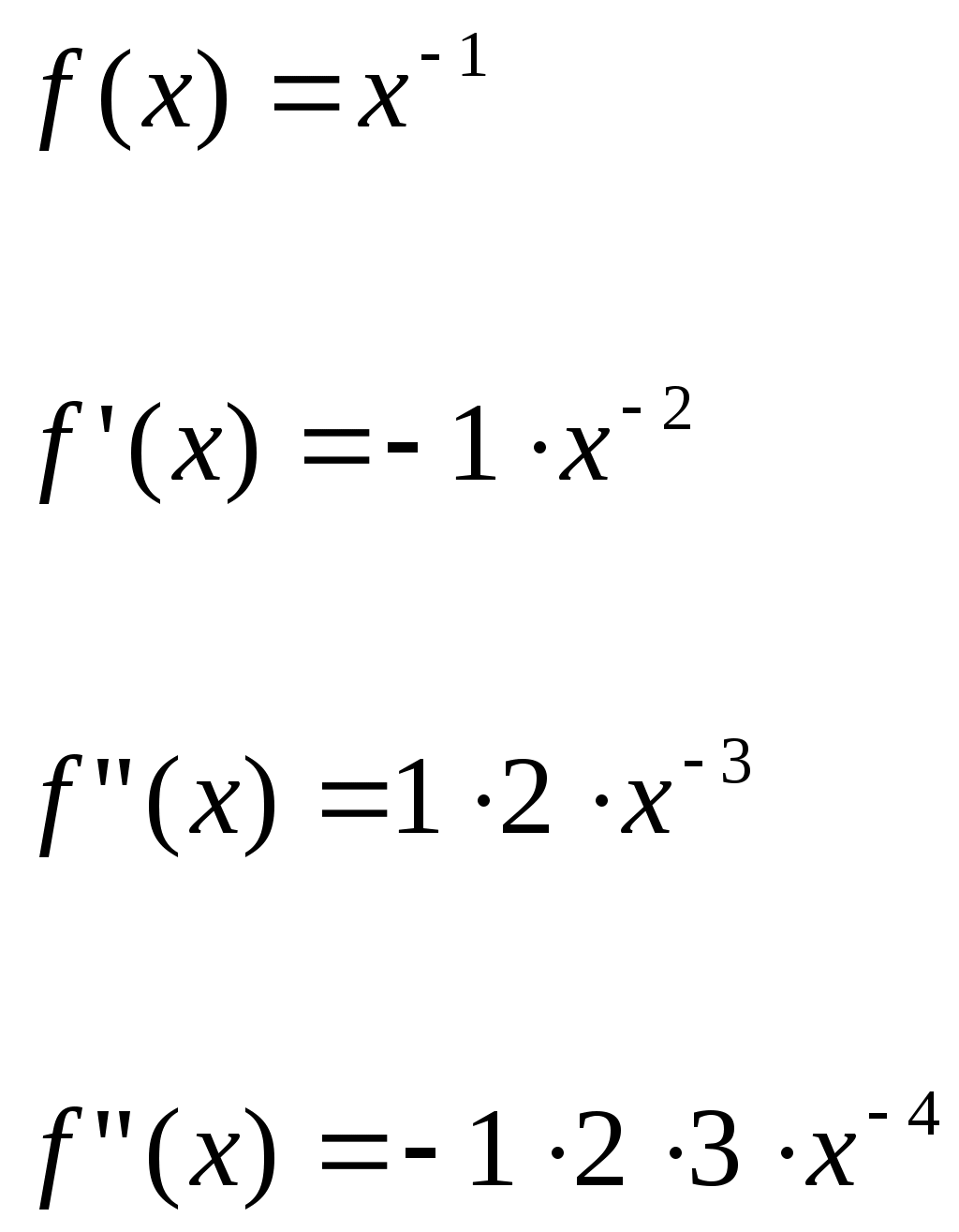
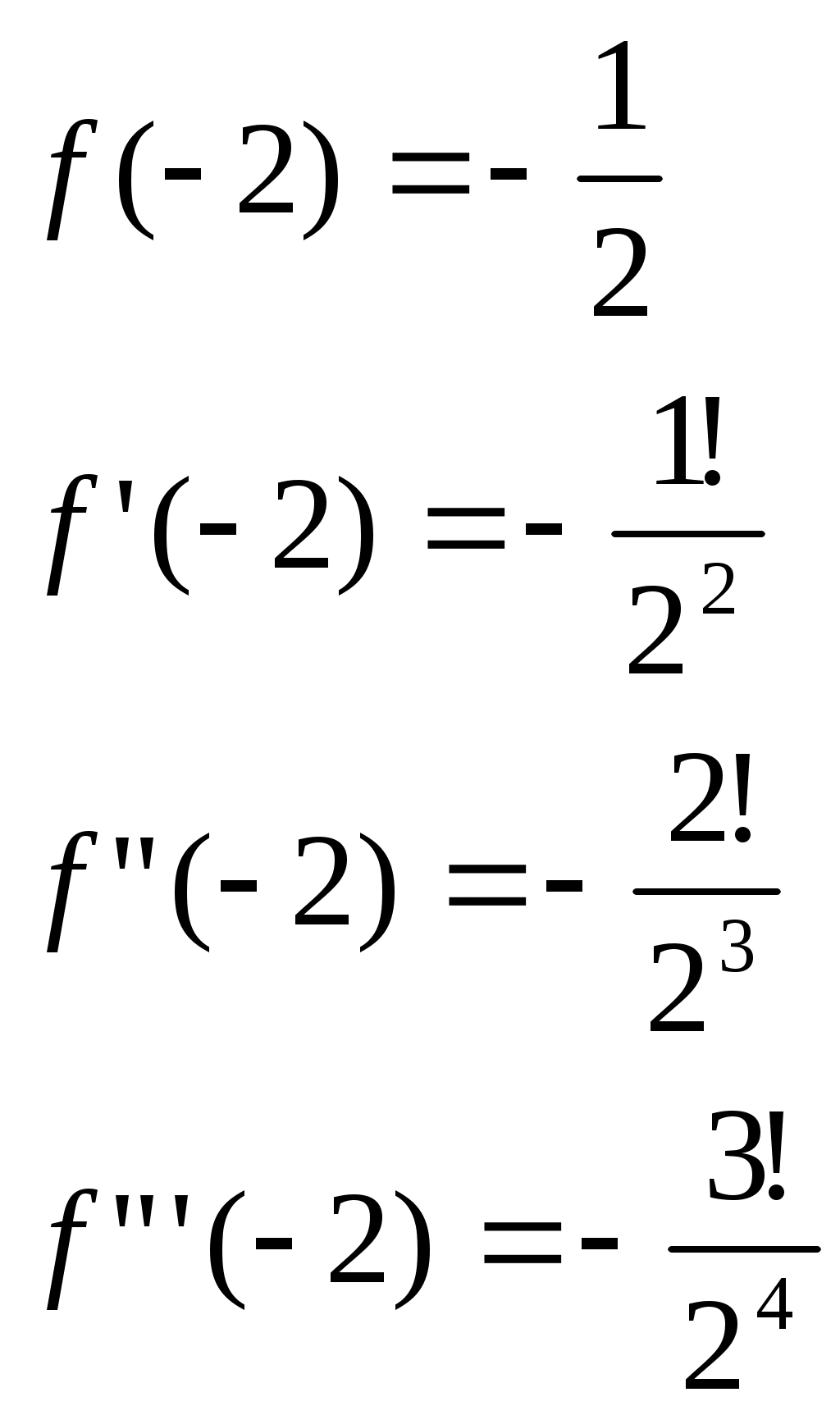
Подставляем эти значения в ряд Тейлора (1) для произвольной функции, получим:
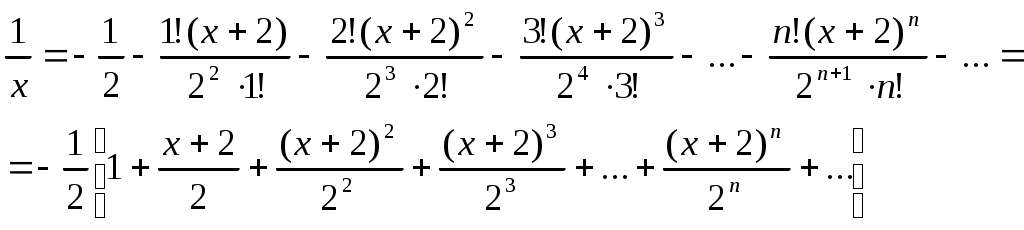
Исследуем сходимость полученного ряда по признаку Даламбера.
; 
; 
;
, если 
. Решая это неравенство, находим интервал: 
. Границы интервала исследуем особо. Подставляя в ряд 
, затем 
, получим числовые ряды 
и 
, которые расходятся, так как у них не выполняется необходимое условие сходимости ряда 
Следовательно, интервал сходимости полученного ряда Тейлора для данной функции есть (
). Внутри этого интервала, т.е. при , ряд является суммой бесконечно убывающей геометрической прогрессии, т.е. сумма ряда.
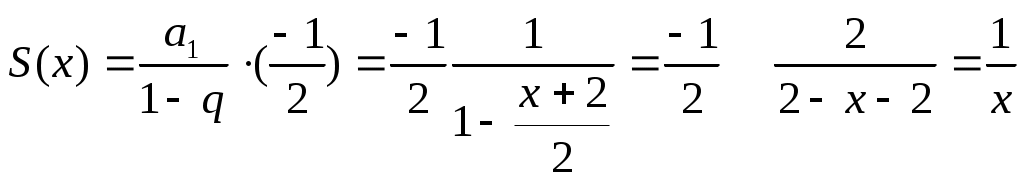, что доказывает сходимость ряда именно к данной функции.
2)
___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___
___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___
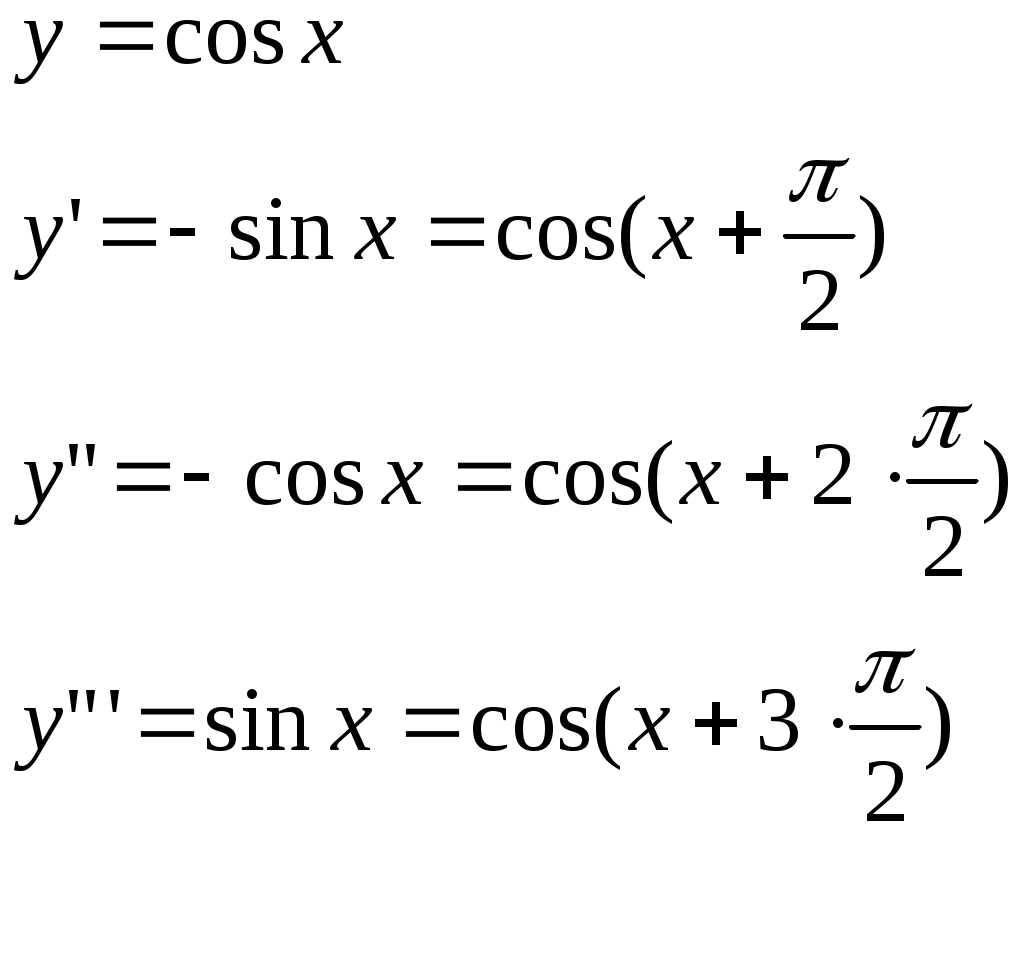
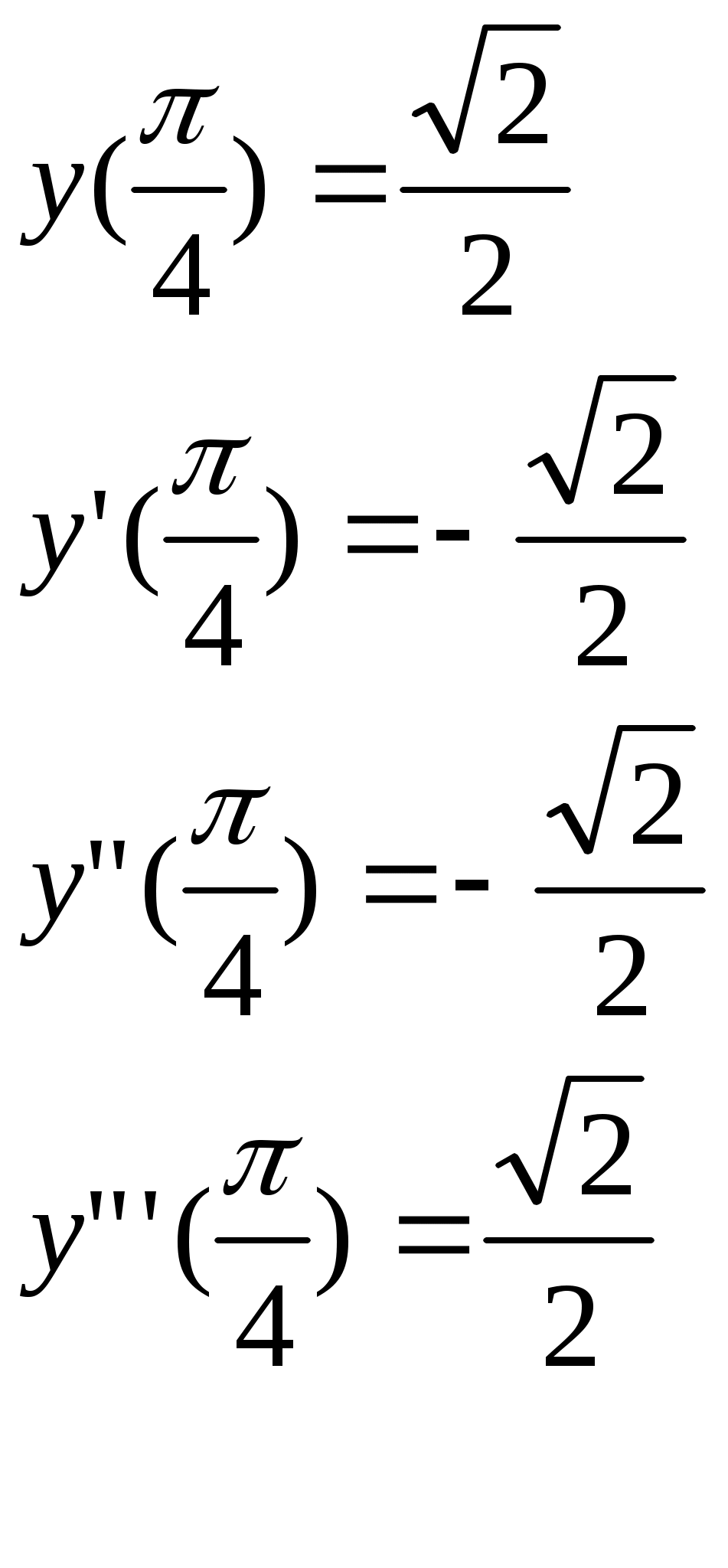
