ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 181
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
X, распределенной по биномиальному закону,
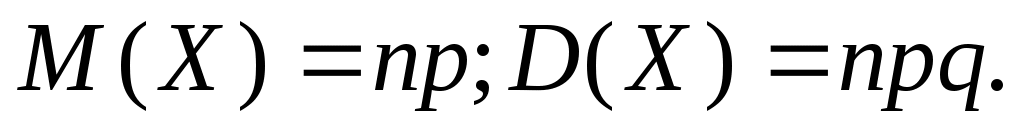
Дискретная случайная величина X называется распределенной по закону Пуассона, если ее возможные значения равны 0, 1, 2, …, m,…, а вероятность того, что , выражается формулой
, выражается формулой
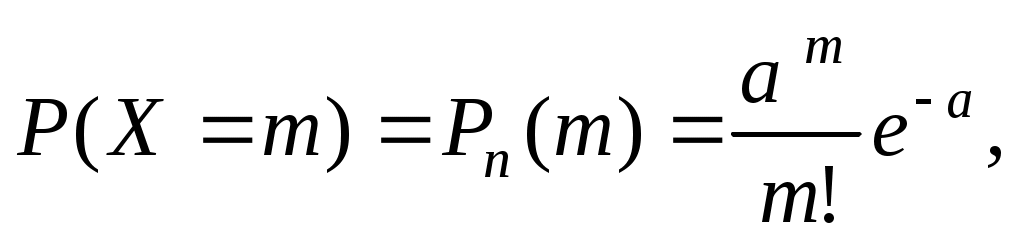
где a – параметр закона Пуассона,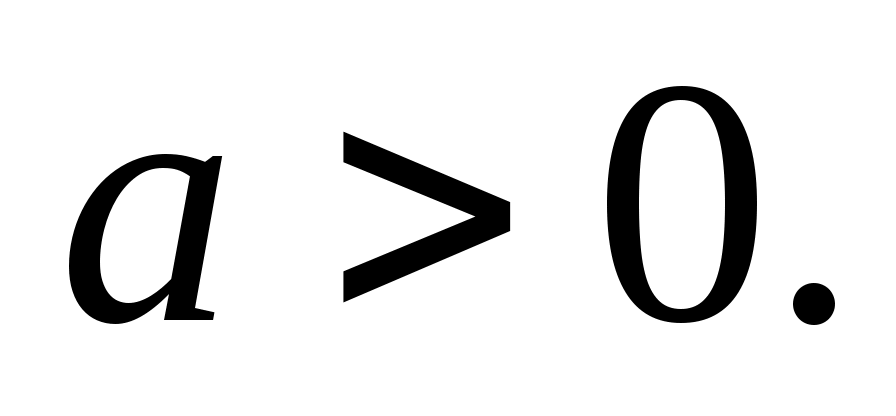
Как было показано ранее, по этой формуле вычисляются вероятности редких событий, т.е. вероятность появления события Am раз при большом числе испытаний n, в каждом из которых вероятность pпоявления события A мала (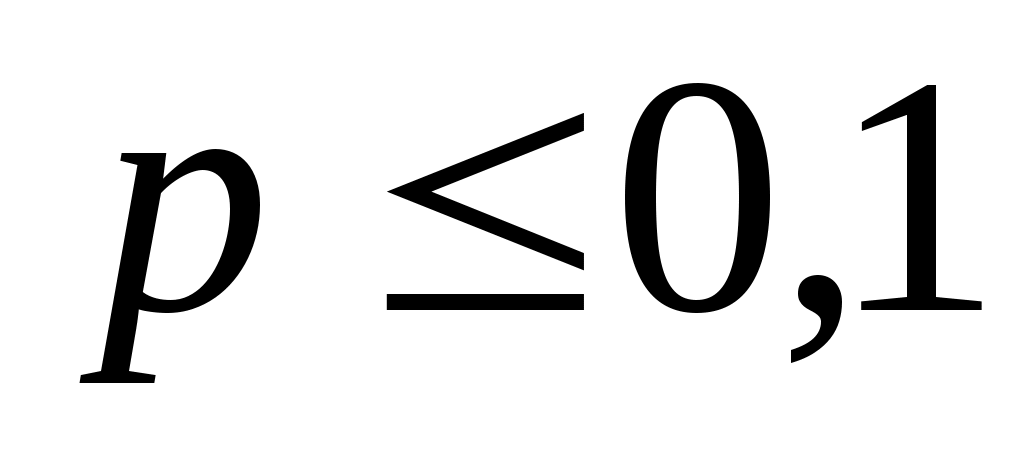 ), однако, произведение
), однако, произведение 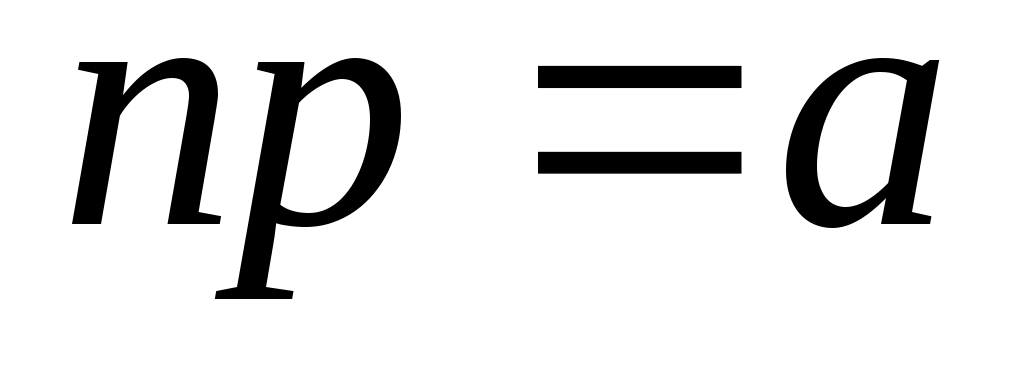 постоянно. Математическое ожидание и дисперсия случайной величины X, распределенной по закону Пуассона,
постоянно. Математическое ожидание и дисперсия случайной величины X, распределенной по закону Пуассона,
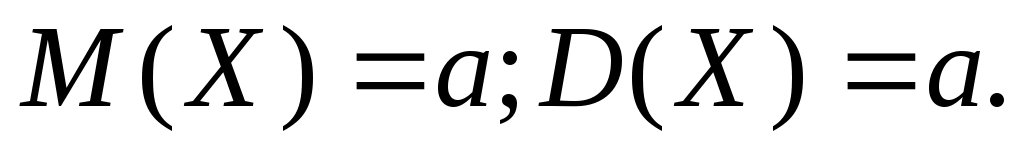
Непрерывная случайная величина Xназывается равномерно распределенной на отрезке [a, b], если ее плотность распределения вероятностей постоянна (т.е. все значения на отрезке случайной величины X равновозможны):
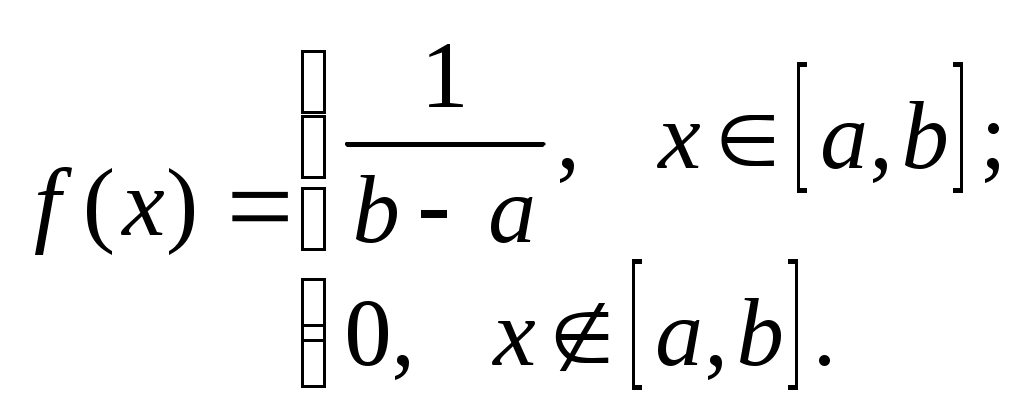
Математическое ожидание и дисперсия СВ, равномерно распределенной на (a,b),
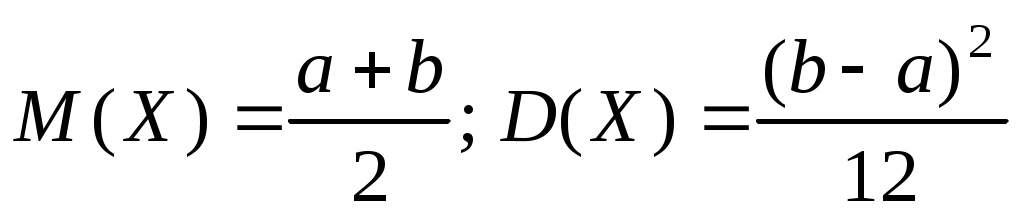 .
.
Непрерывная случайная величина Xназывается распределенной по нормальному закону, если ее плотность распределения вероятностей равна:
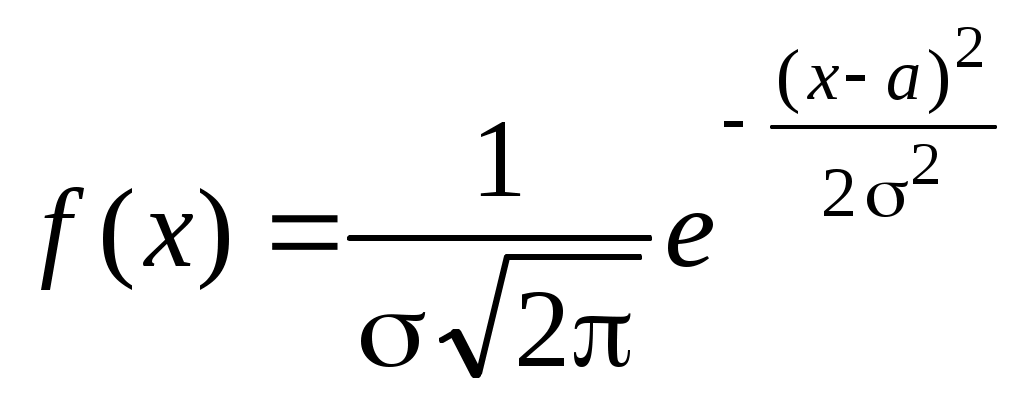 ,
,
где a – математическое ожидание; 2– дисперсия; – среднее квадратичное отклонение случайной величины X (a, – параметры нормального распределения).
Вероятность попадания случайной величины
X, распределенной по нормальному закону, в интервал (, )
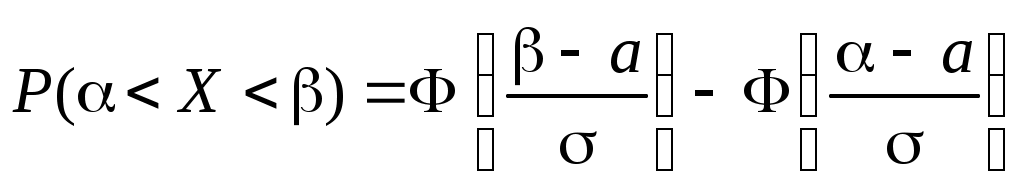 ,
,
где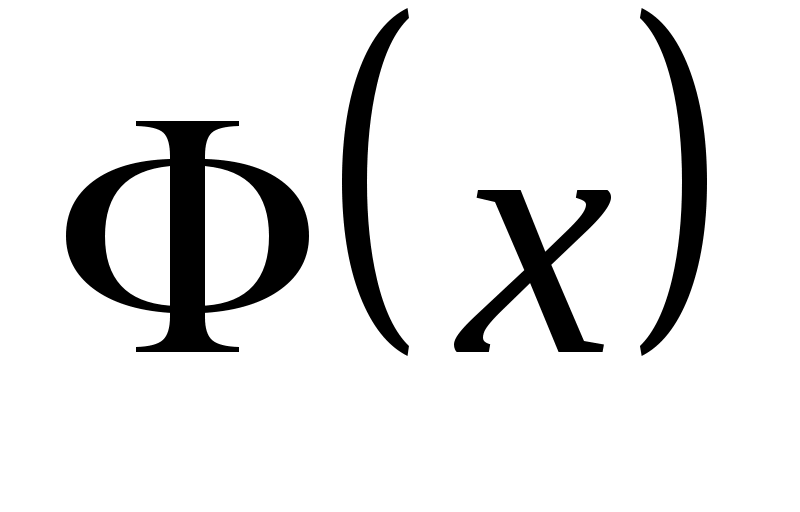 – функция Лапласа.
– функция Лапласа.
Вероятность того, что абсолютная величина отклонения меньше постоянного числа ε,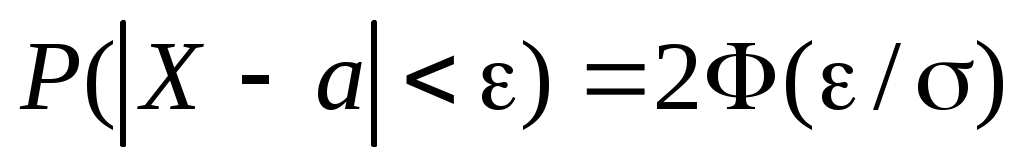 .
.
Следствие. Правило «трех сигм»: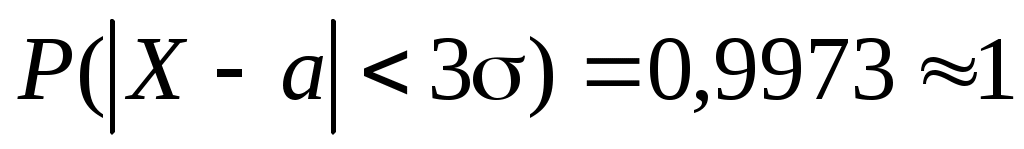 .
.
Пример 13. Случайная величина Xраспределена по нормальному закону с параметрами a = 2, = 5.
Найти вероятность того, что случайная величина X примет значение в интервале (1, 4).
Решение. По условию = 1, = 4,a = 2, = 5. Тогда
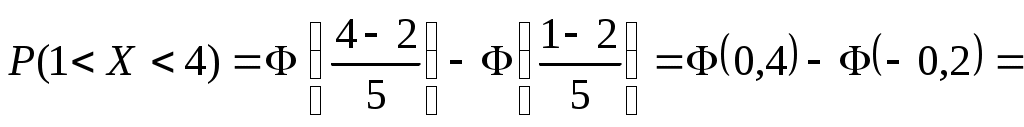
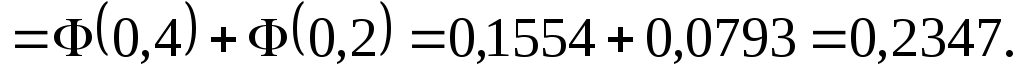
Система двух случайных величин – совокупность двух случайных величин (X,Y), которые рассматриваются одновременно.
Измерения обычно осуществляются попарно, а полученные значения случайных величин X и Y в определенном смысле взаимосвязаны.
Закон распределения двумерной случайной величины дискретного типа представляет собой перечень значений этой величины и их вероятностей, указанных в специальной таблице. В табл.1 представлены возможные значения (xi,yj) и их совместные вероятности:
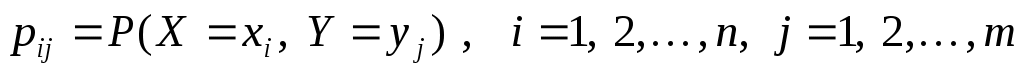 .
.
Таблица 1
Закон распределения двумерной случайной величины
Зная закон распределения дискретной двумерной случайной величины (X, Y), можно найти закон распределения каждой случайной величины X и Y:
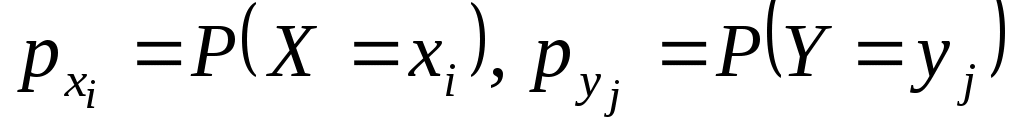 ;
;
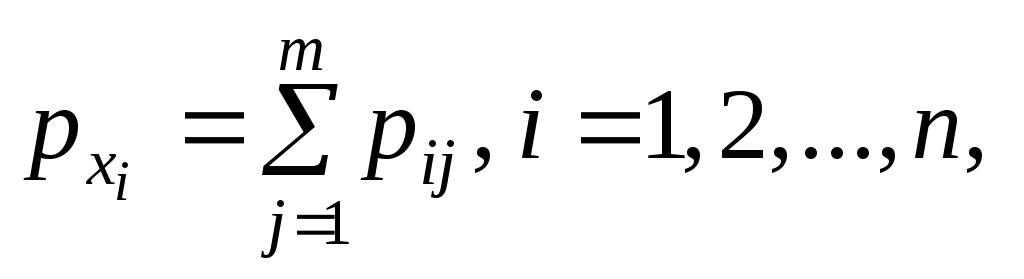
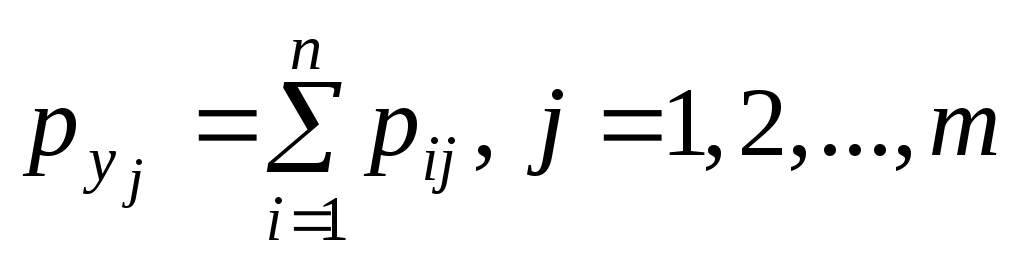 .
.
Интегральная функция распределения двумерной случайной величины (X, Y) есть вероятность совместного выполнения неравенств X < x и Y < y, т.е.
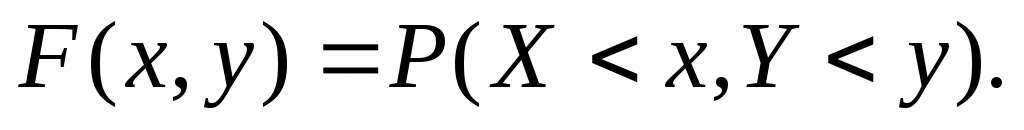
Двумерная случайная величина непрерывного типа может быть задана интегральной или дифференциальной функцией распределения. Если интегральная функция распределения всюду непрерывна и имеет непрерывную смешанную частную производную второго порядка, то дифференциальная функция распределения системы двух случайных величин (X, Y) определяется по формуле
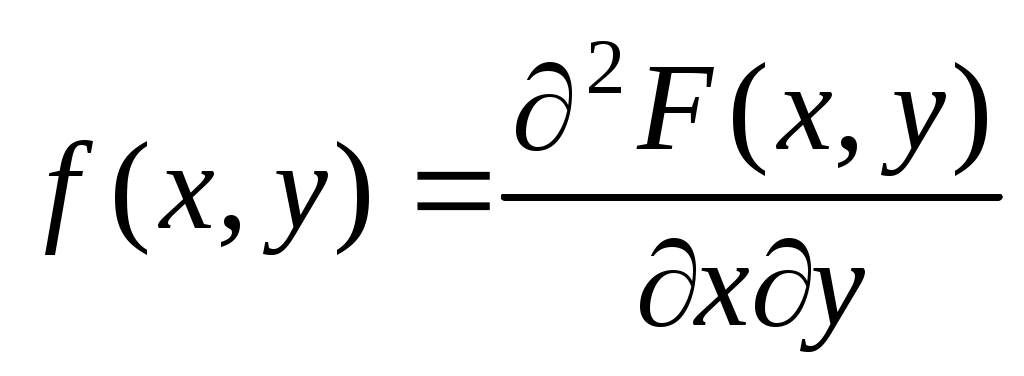 .
.
Плотность распределения отдельных случайных величин, входящих в систему, выражается через плотность системы случайных величин следующим образом:
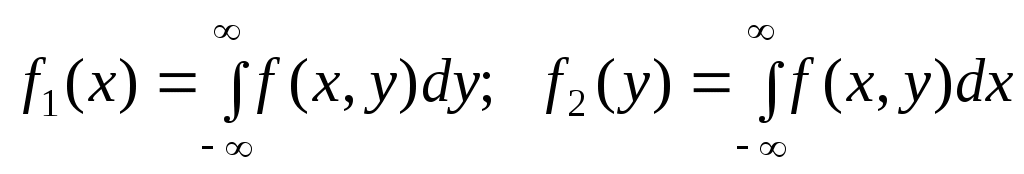 .
.
Условный закон распределения случайной величины, входящей в систему, есть закон ее распределения, полученный в предположении, что другая случайная величина приняла определенное значение. Для системы случайных величин дискретного типа условные законы распределения имеют вид
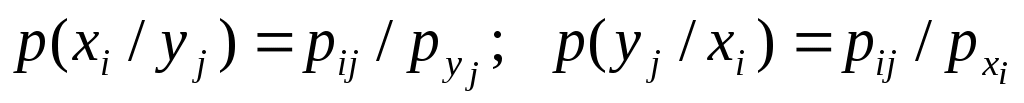 .
.
Условные математические ожидания (условные средние) дискретных случайных величин
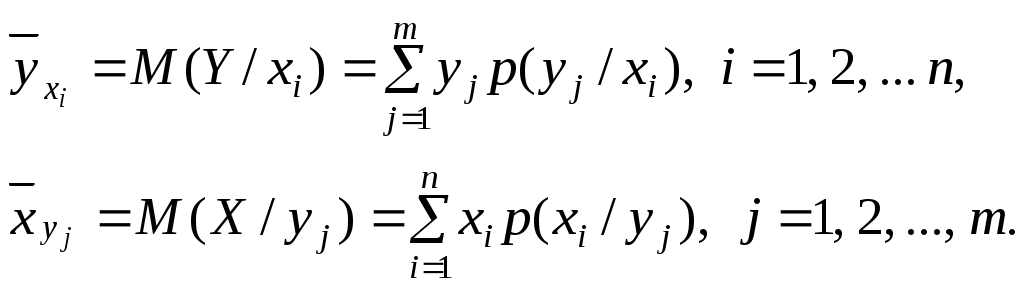
Условные распределения показывают, что одна СВ реагирует на изменение другой изменением своего закона распределения. Такая общая зависимость называется стохастической (вероятностной
) и достаточно сложна для изучения. Однако зависимость условного среднего одной СВ от значений другой является функцией, которая называется регрессией: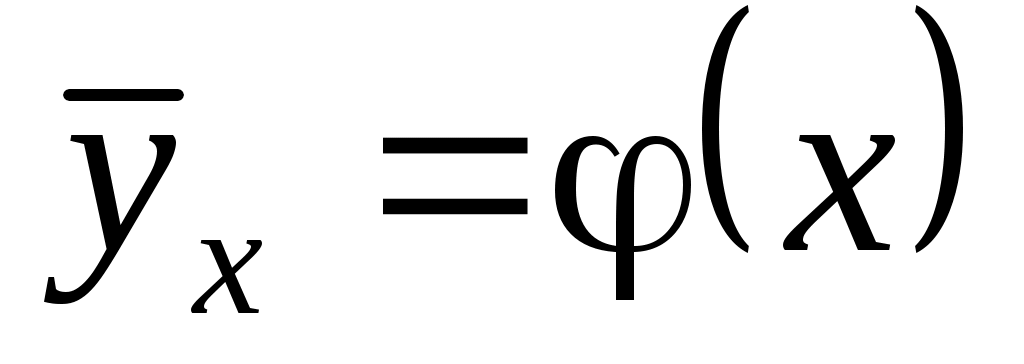 – регрессия Y на X,
– регрессия Y на X, 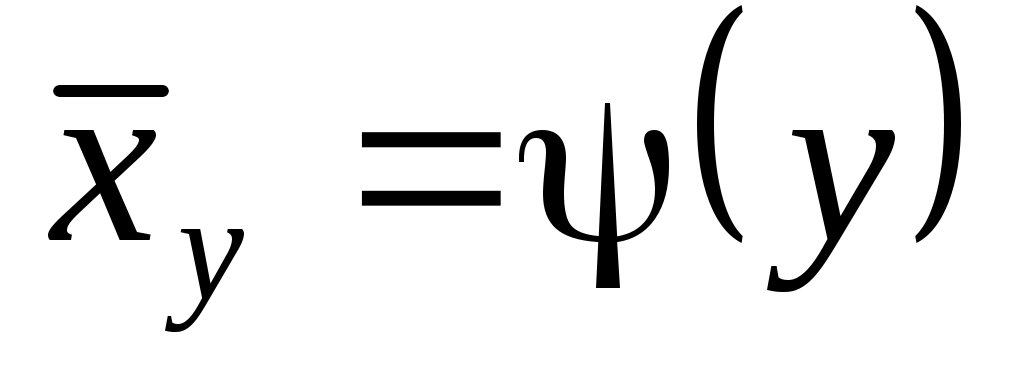 – регрессия X на Y. Но и функции регрессии в общем случае достаточно сложны, поэтому используют различные их приближения, например линейной функцией (наилучшей в смысле наименьшего значения среднего квадрата отклонения). Это значит, что для регрессии Y на X функция
– регрессия X на Y. Но и функции регрессии в общем случае достаточно сложны, поэтому используют различные их приближения, например линейной функцией (наилучшей в смысле наименьшего значения среднего квадрата отклонения). Это значит, что для регрессии Y на X функция 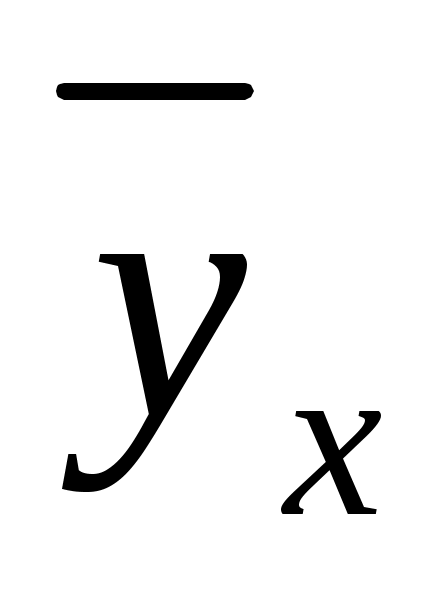 приближается линейной функцией
приближается линейной функцией 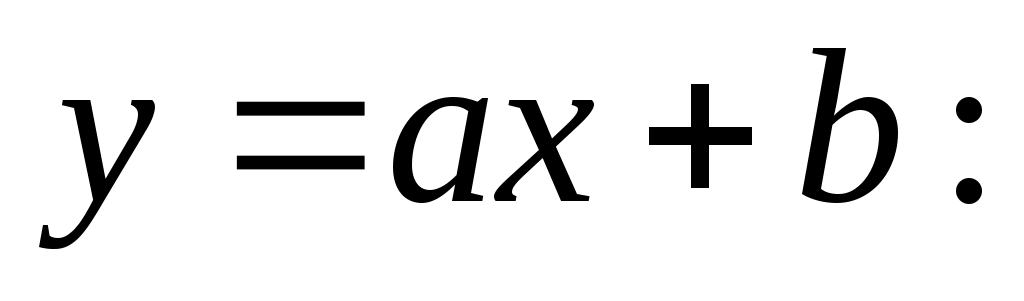
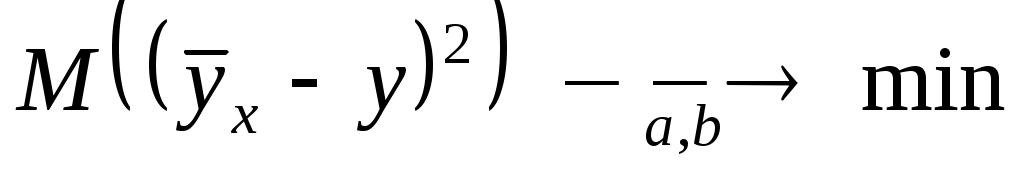 .
.
Уравнения таких наилучших линейных регрессий
для регрессии Y на X
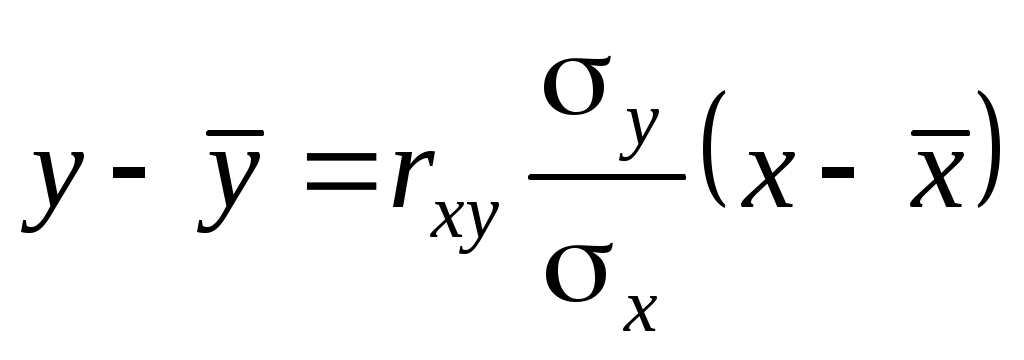 ;
;
для регрессии X на Y
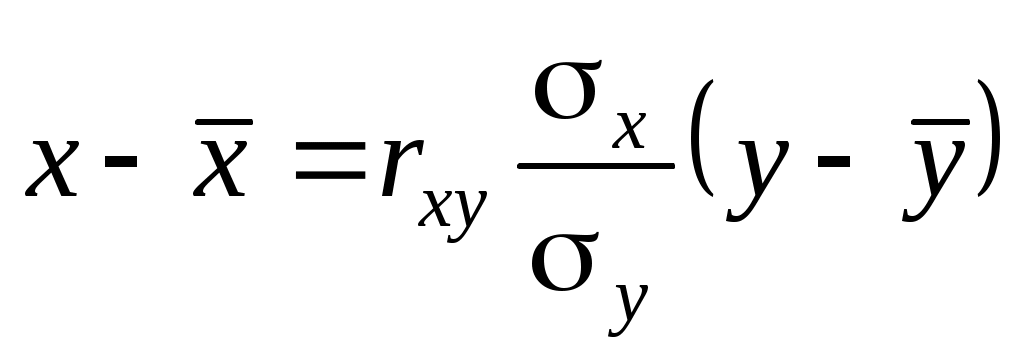 ,
,
где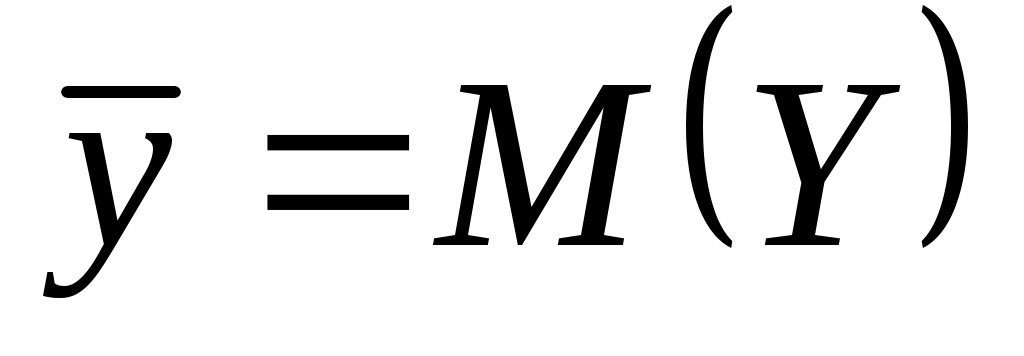 ,
, 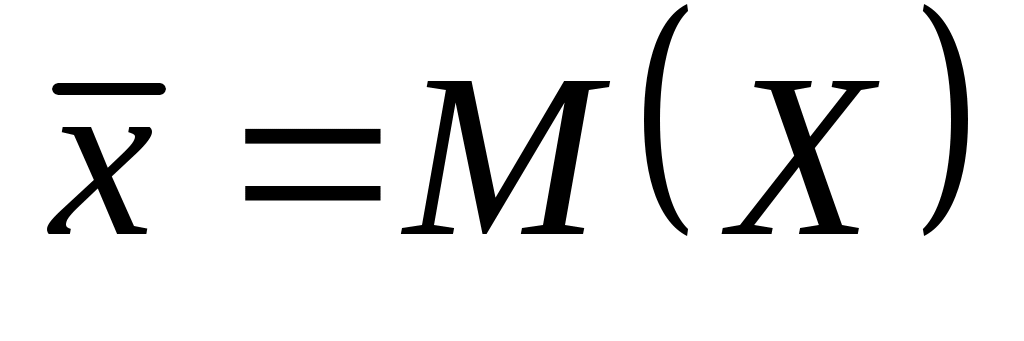 ,
, 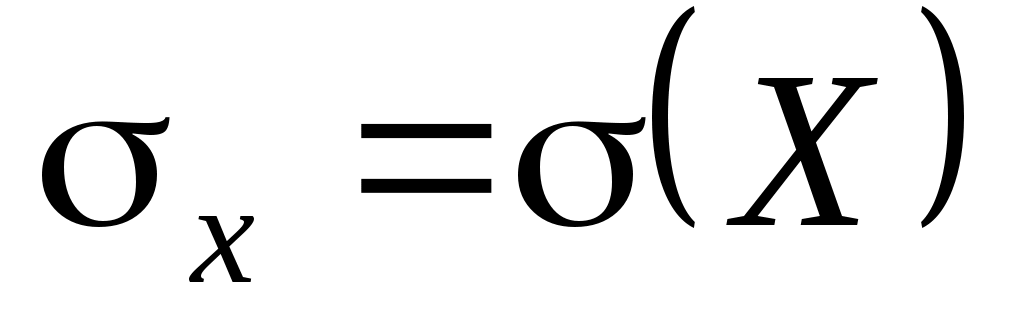 ,
, 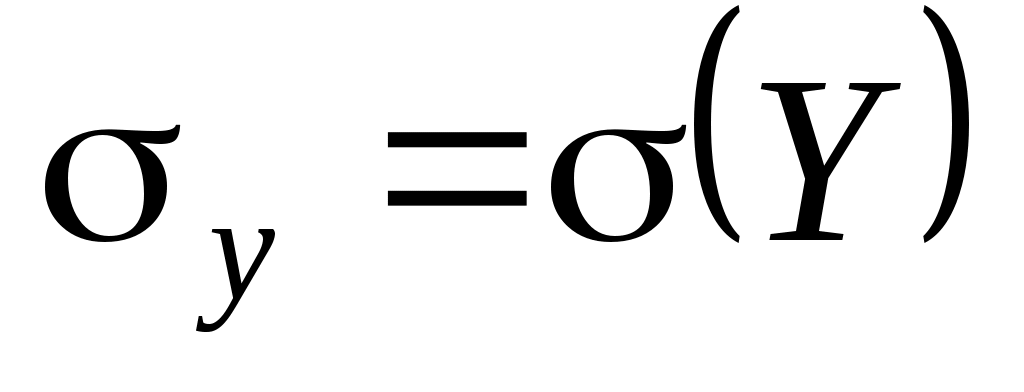 .
.
Коэффициент корреляции
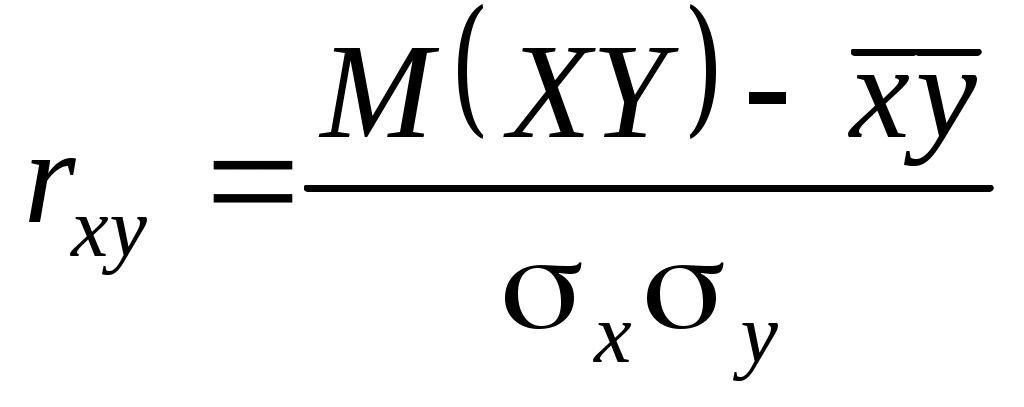
характеризует близость (или тесноту) связи между случайными величинами к линейной.
Отметим, что всегда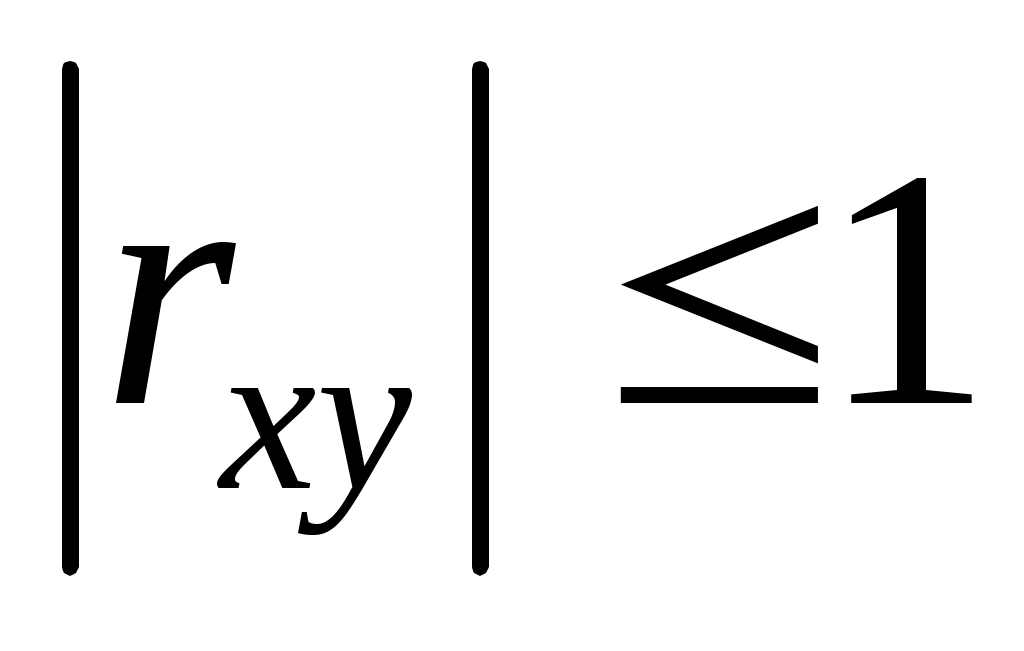 . Если
. Если 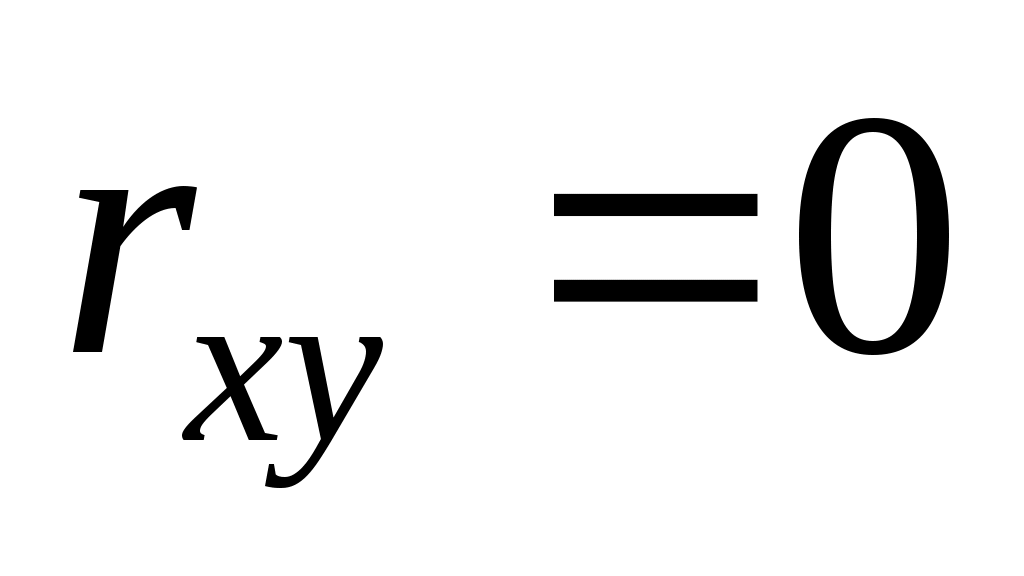 , то СВ называются некоррелированными и в этом случае их условные средние значения являются постоянными, т.е. не зависят от значений другой СВ, что характеризует их слабую взаимозависимость. Если
, то СВ называются некоррелированными и в этом случае их условные средние значения являются постоянными, т.е. не зависят от значений другой СВ, что характеризует их слабую взаимозависимость. Если 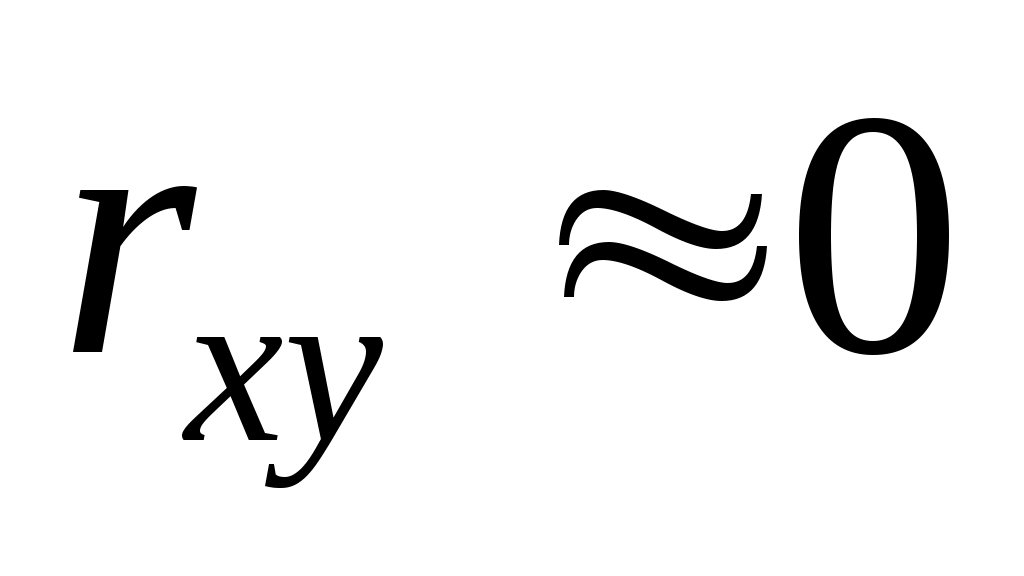 (угол между прямыми наилучших линейных регрессий близок к прямому), связь между случайными величинами достаточно слабая и нелинейная. Если
(угол между прямыми наилучших линейных регрессий близок к прямому), связь между случайными величинами достаточно слабая и нелинейная. Если
Дискретная случайная величина X называется распределенной по закону Пуассона, если ее возможные значения равны 0, 1, 2, …, m,…, а вероятность того, что
где a – параметр закона Пуассона,
Как было показано ранее, по этой формуле вычисляются вероятности редких событий, т.е. вероятность появления события Am раз при большом числе испытаний n, в каждом из которых вероятность pпоявления события A мала (
Непрерывная случайная величина Xназывается равномерно распределенной на отрезке [a, b], если ее плотность распределения вероятностей постоянна (т.е. все значения на отрезке случайной величины X равновозможны):
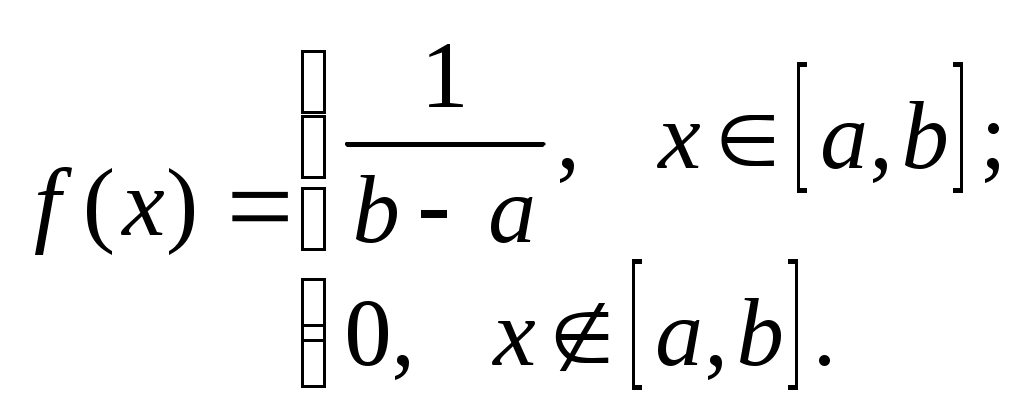
Математическое ожидание и дисперсия СВ, равномерно распределенной на (a,b),
Непрерывная случайная величина Xназывается распределенной по нормальному закону, если ее плотность распределения вероятностей равна:
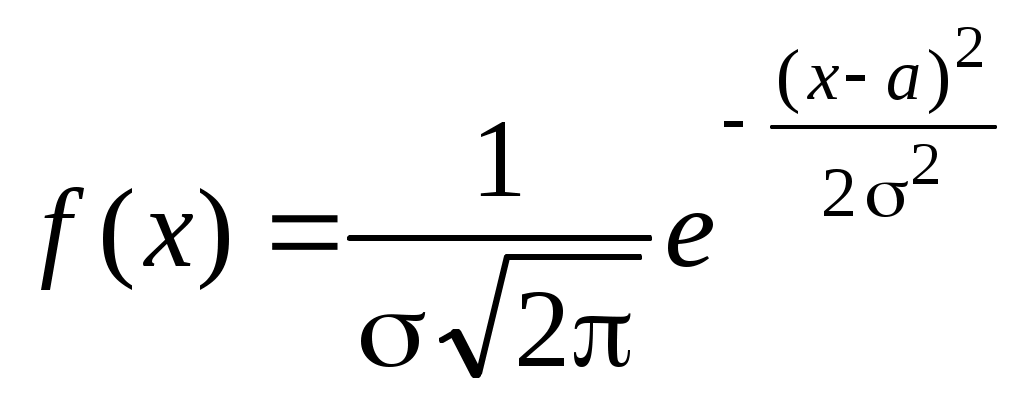 ,
,где a – математическое ожидание; 2– дисперсия; – среднее квадратичное отклонение случайной величины X (a, – параметры нормального распределения).
Вероятность попадания случайной величины
X, распределенной по нормальному закону, в интервал (, )
где
Вероятность того, что абсолютная величина отклонения меньше постоянного числа ε,
Следствие. Правило «трех сигм»:
Пример 13. Случайная величина Xраспределена по нормальному закону с параметрами a = 2, = 5.
Найти вероятность того, что случайная величина X примет значение в интервале (1, 4).
Решение. По условию = 1, = 4,a = 2, = 5. Тогда
1.4. Система двух случайных величин и регрессия
Система двух случайных величин – совокупность двух случайных величин (X,Y), которые рассматриваются одновременно.
Измерения обычно осуществляются попарно, а полученные значения случайных величин X и Y в определенном смысле взаимосвязаны.
Закон распределения двумерной случайной величины дискретного типа представляет собой перечень значений этой величины и их вероятностей, указанных в специальной таблице. В табл.1 представлены возможные значения (xi,yj) и их совместные вероятности:
Таблица 1
Закон распределения двумерной случайной величины
| Y | X | ||||||
| x1 | x2 | … | xi | … | xn | pyj | |
| | | | | | | | |
| y1 | p11 | p21 | … | pi1 | … | pn1 | py1 |
| y2 | p12 | p22 | … | pi2 | … | pn2 | py2 |
| … | … | … | … | … | … | … | … |
| yj | p1j | p2j | … | pij | … | pnj | pyj |
| … | … | … | … | … | … | … | … |
| ym | p1m | p2m | … | pim | … | pnm | pym |
| pxi | px1 | px2 | … | pxi | … | pxn | |
Зная закон распределения дискретной двумерной случайной величины (X, Y), можно найти закон распределения каждой случайной величины X и Y:
Интегральная функция распределения двумерной случайной величины (X, Y) есть вероятность совместного выполнения неравенств X < x и Y < y, т.е.
Двумерная случайная величина непрерывного типа может быть задана интегральной или дифференциальной функцией распределения. Если интегральная функция распределения всюду непрерывна и имеет непрерывную смешанную частную производную второго порядка, то дифференциальная функция распределения системы двух случайных величин (X, Y) определяется по формуле
Плотность распределения отдельных случайных величин, входящих в систему, выражается через плотность системы случайных величин следующим образом:
Условный закон распределения случайной величины, входящей в систему, есть закон ее распределения, полученный в предположении, что другая случайная величина приняла определенное значение. Для системы случайных величин дискретного типа условные законы распределения имеют вид
Условные математические ожидания (условные средние) дискретных случайных величин
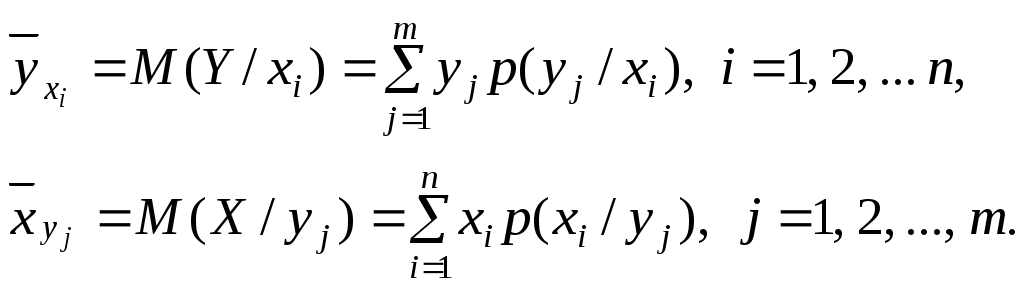
Условные распределения показывают, что одна СВ реагирует на изменение другой изменением своего закона распределения. Такая общая зависимость называется стохастической (вероятностной
) и достаточно сложна для изучения. Однако зависимость условного среднего одной СВ от значений другой является функцией, которая называется регрессией:
Уравнения таких наилучших линейных регрессий
для регрессии Y на X
для регрессии X на Y
где
Коэффициент корреляции
характеризует близость (или тесноту) связи между случайными величинами к линейной.
Отметим, что всегда