Файл: А. П. Господариков, И. А. Лебедев.doc

:

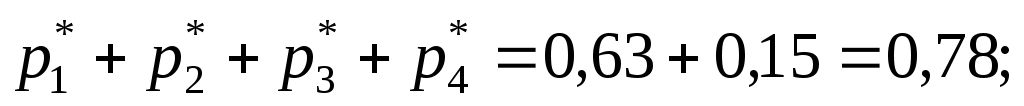
за , , , , :

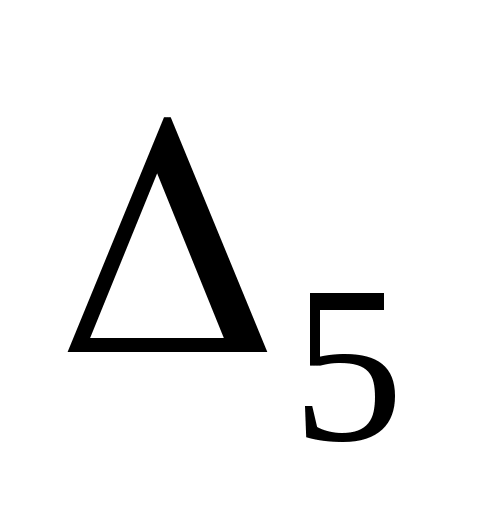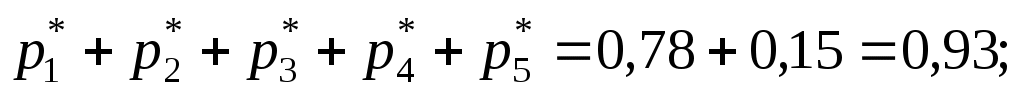
за все интервалы : .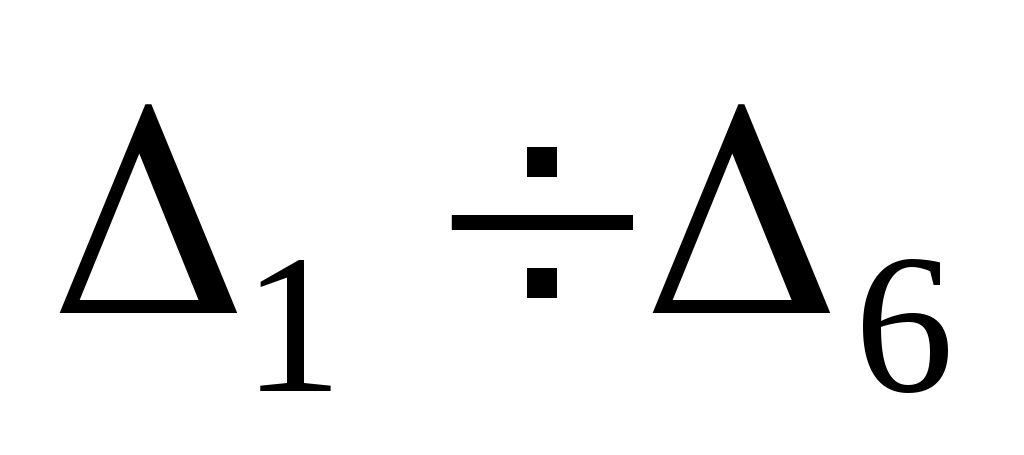

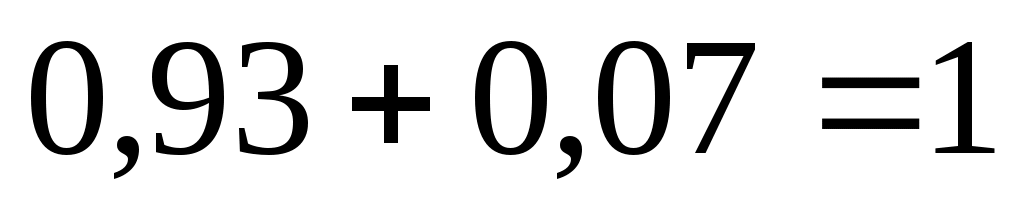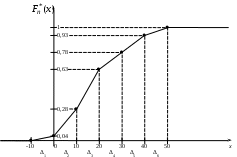
Для построения графика эмпирической функции распределения, найденные значения накопленной вероятности следует отложить по вертикальной оси в правых концах соответствующих по номерам интервалов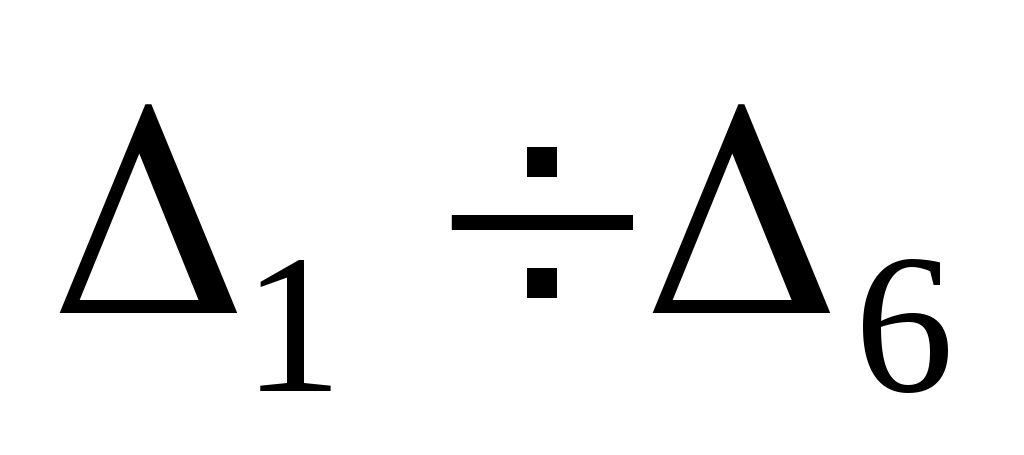 . Полученные точки необходимо соединить отрезками, причем слева от функция 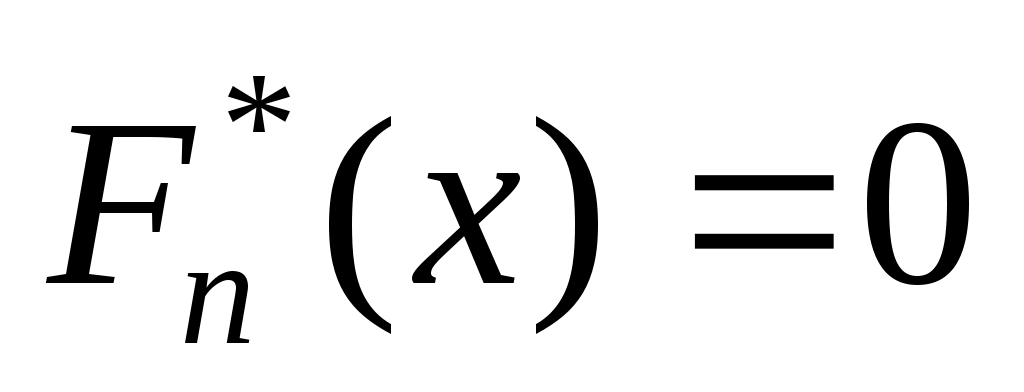, а справа от 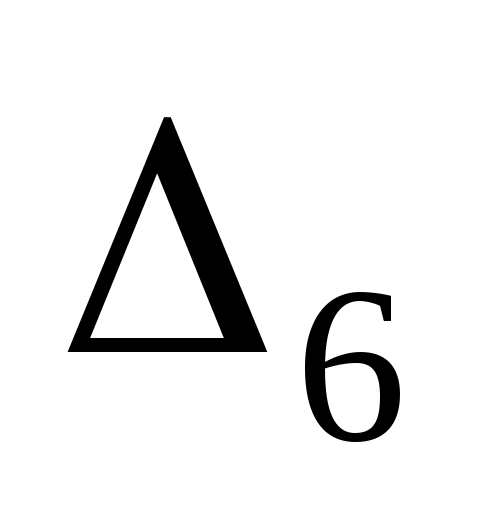функция 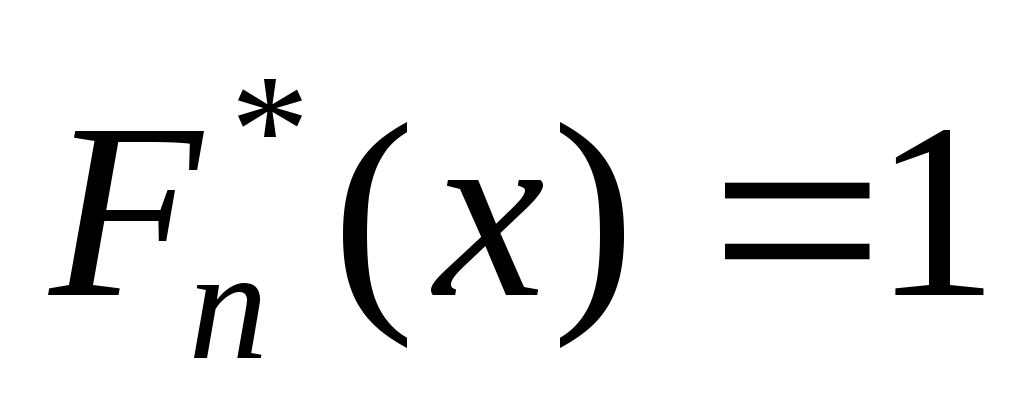(рис.5).

О
Рис.5. Эмпирическая функция

распределения
пределяем эмпирические плотности:







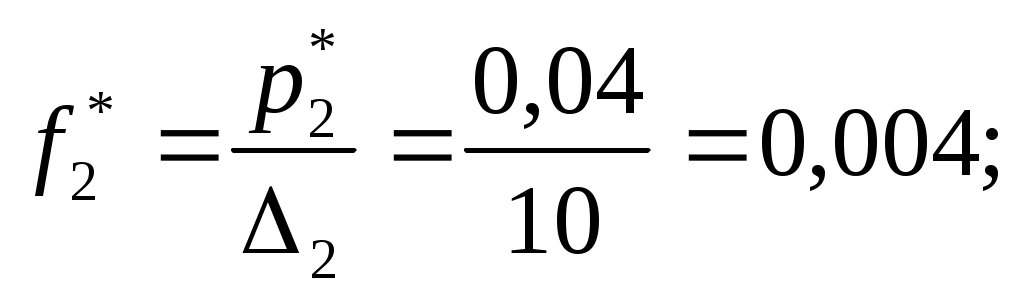
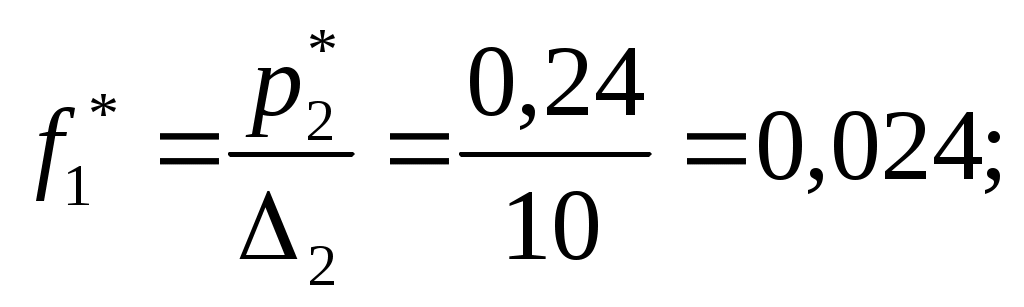
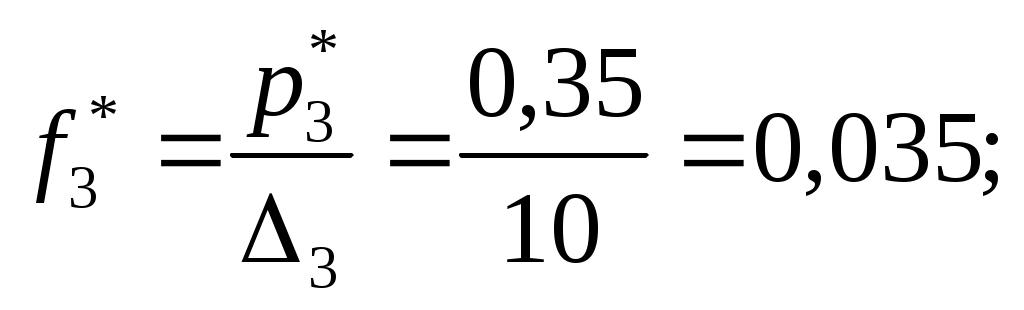
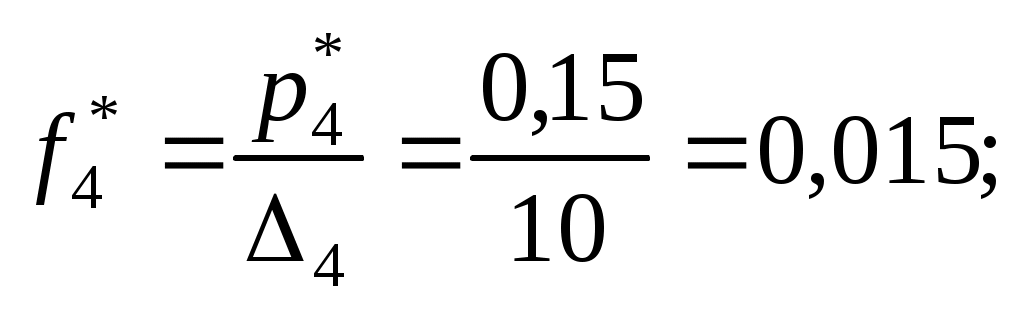
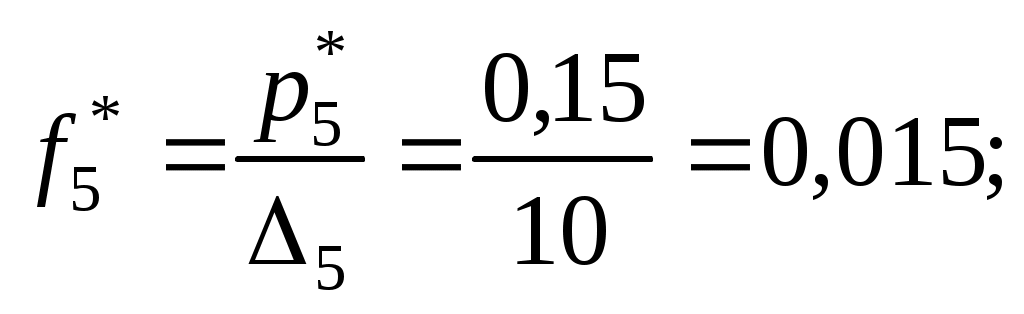
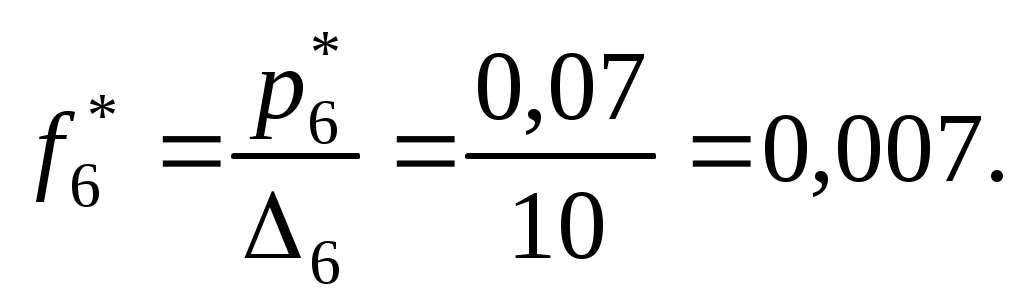
Строим гистограмму (рис.6).



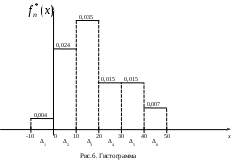
По вариационному ряду (в том числе, сгруппированному) вычисляются основные эмпирические или выборочные характеристики: выборочное среднее

---

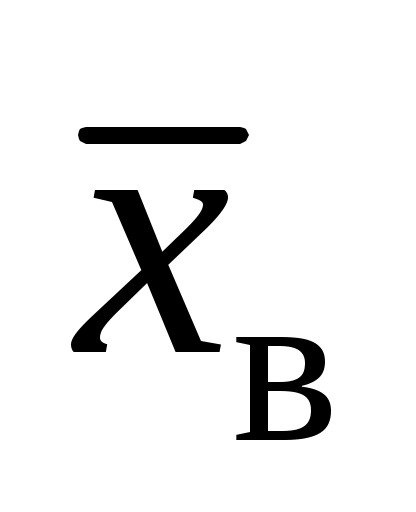, выборочная дисперсия 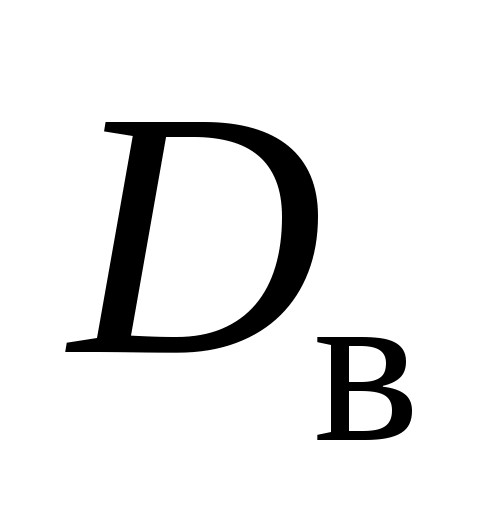и выборочное отклонение :

; ; .

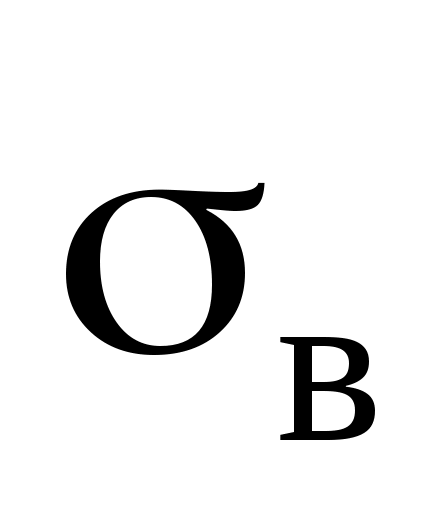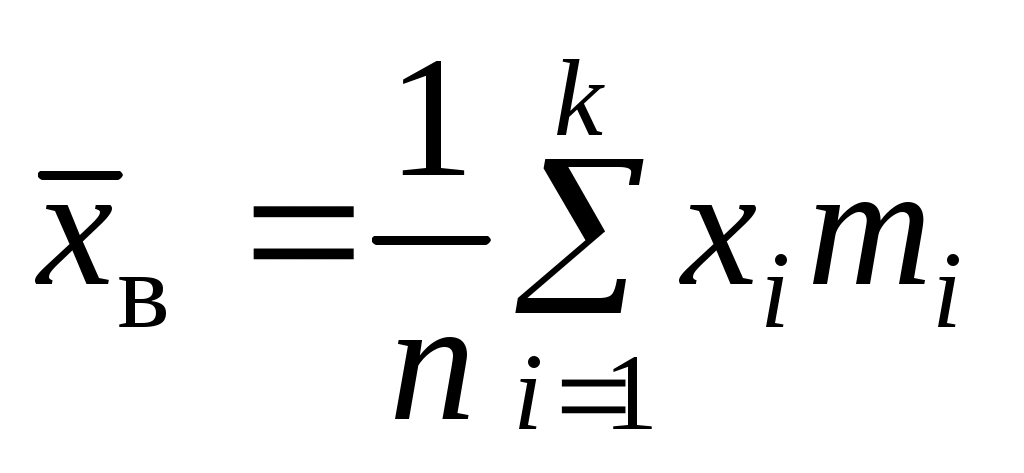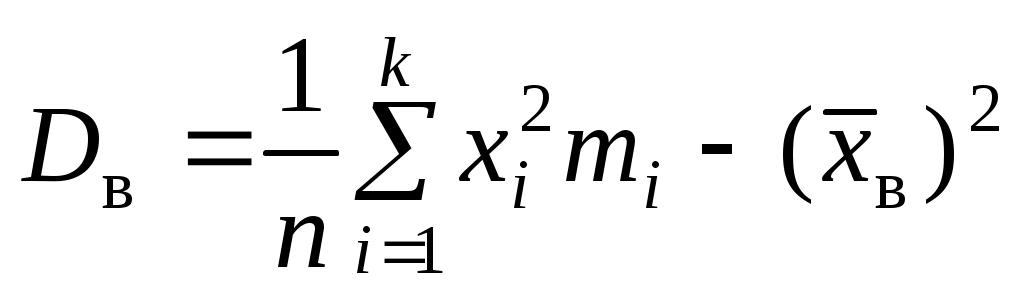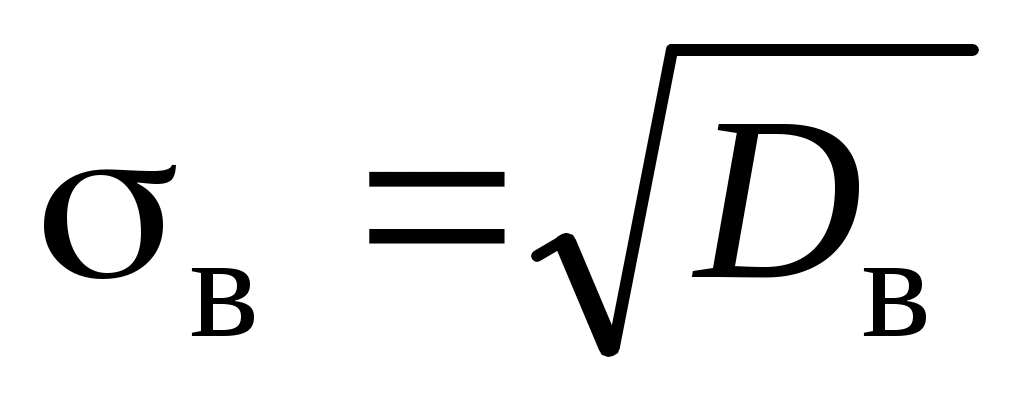Для каждой выборочной характеристики получается одно определенное значение (точка), которая является приближением соответствующей неизвестной характеристик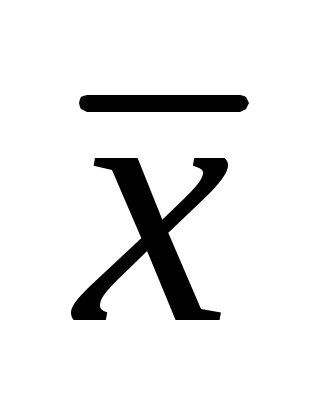и или 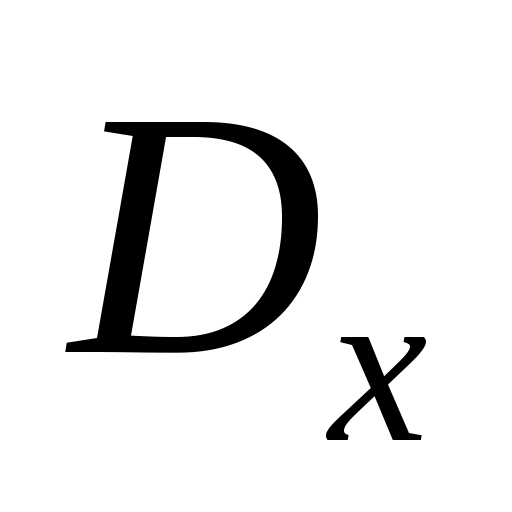случайной величины X. Поэтому эти приближения называют точечными оценками характеристик (или параметров) неизвестного распределения. По закону больших чисел эти точечные оценки сходятся к соответствующим неизвестным значениям: 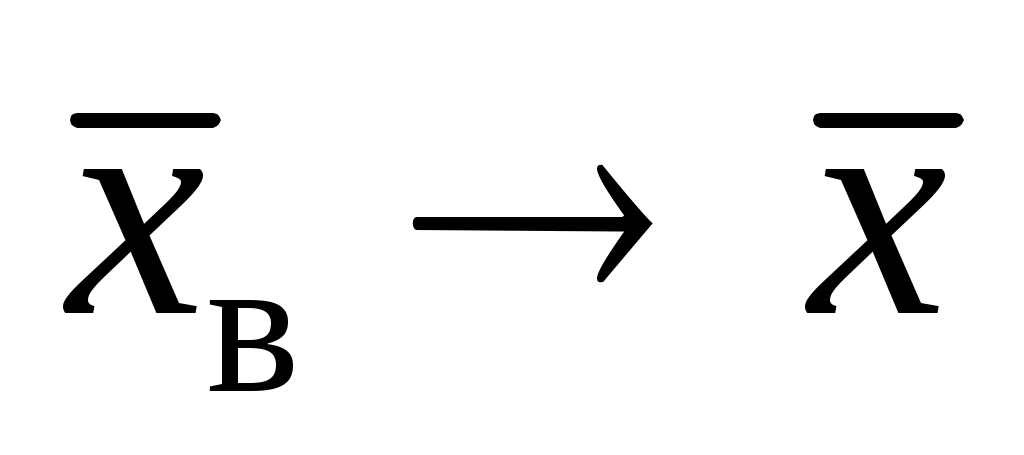, при , т.е. эти оценки являются состоятельными. Кроме того, выборочное среднее является несмещенной оценкой, т.е. его математическое ожидание (среднее!) равно неизвестному значению 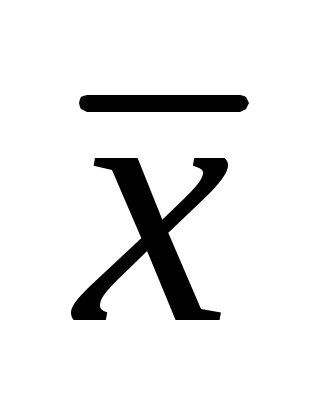: 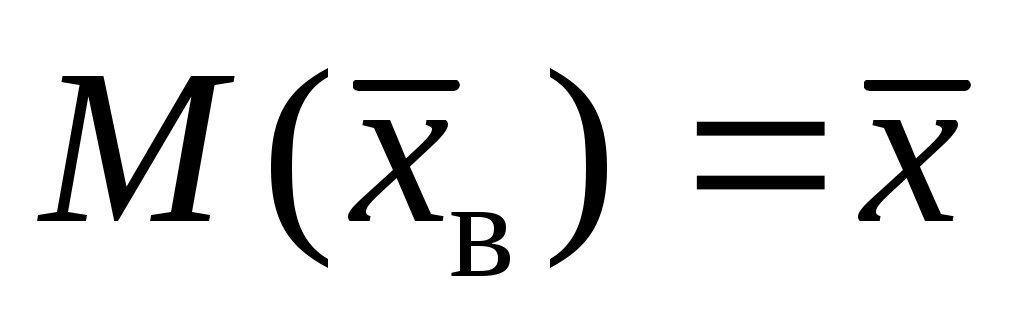. Выборочная дисперсия является смещенной оценкой: 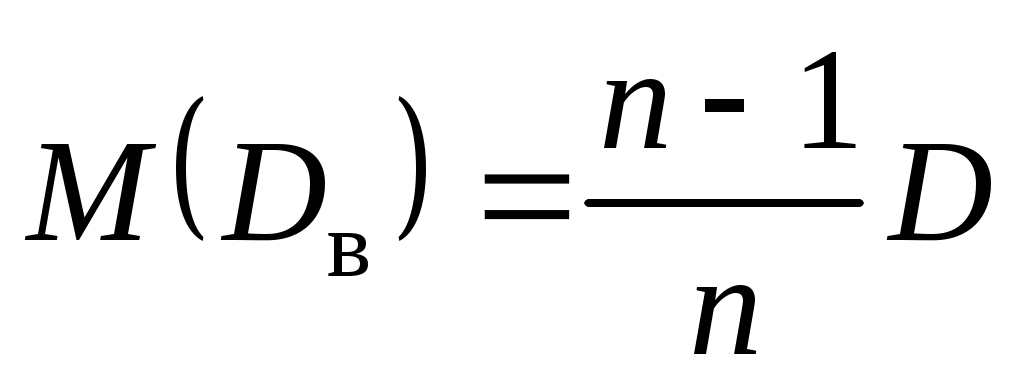. 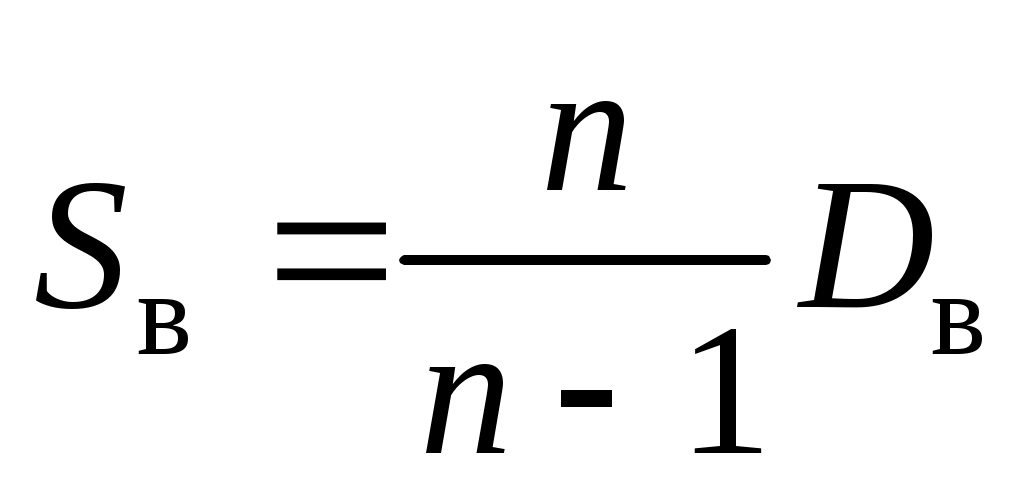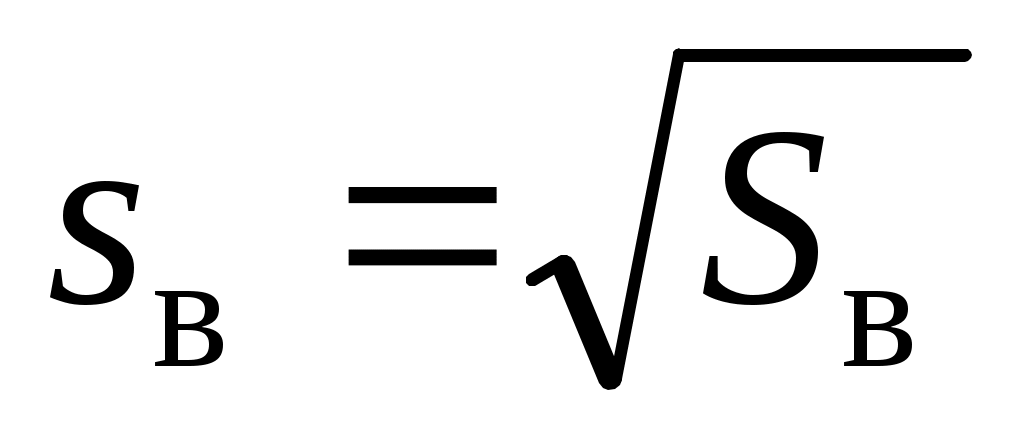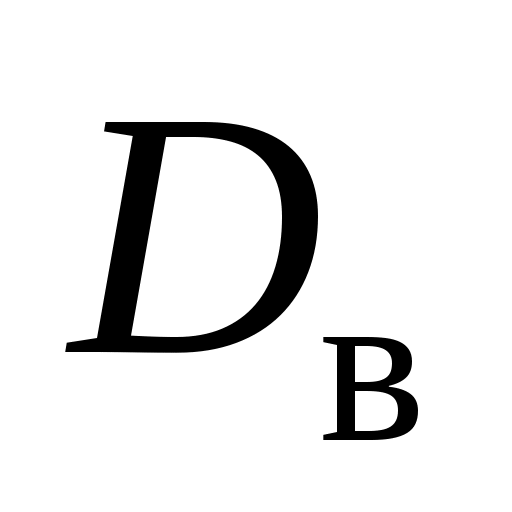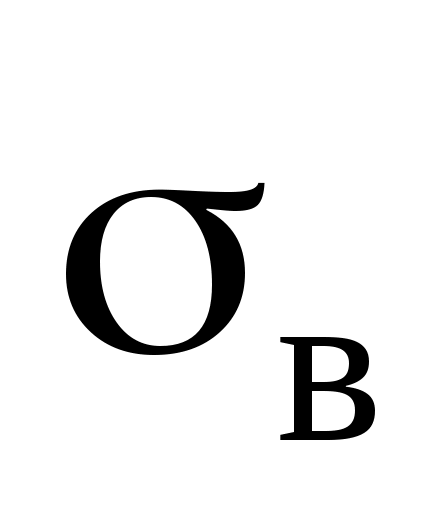В результате при небольших объемах (n < 30) часто рассматривают исправленные дисперсию и отклонение вместо и соответственно.

Другой способ оценки неизвестных характеристик или параметров распределения заключается в указании интервала, куда попадает неизвестное значение с заданной вероятностью (или с заданной надежностью):

---

,

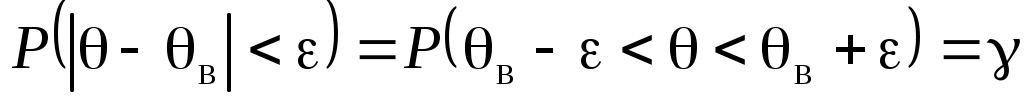где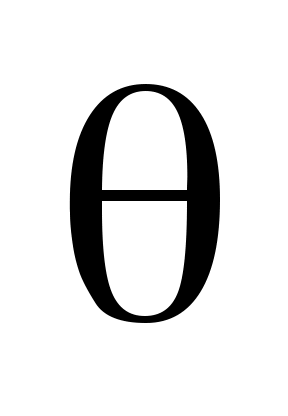 – неизвестное значение; 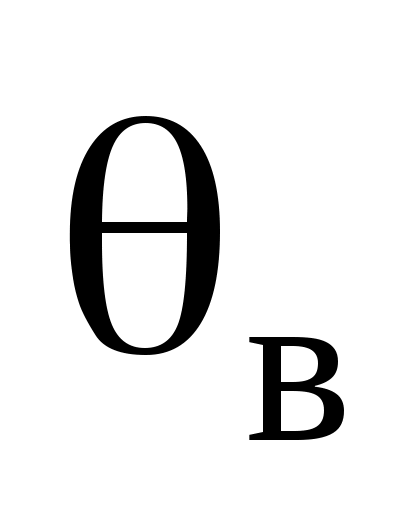– выборочное значение; 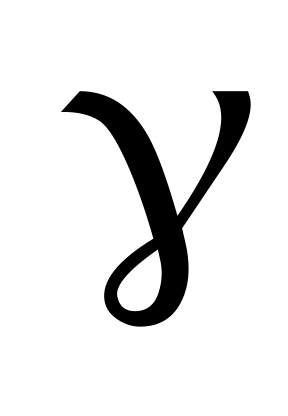– надежность (или доверительная вероятность); 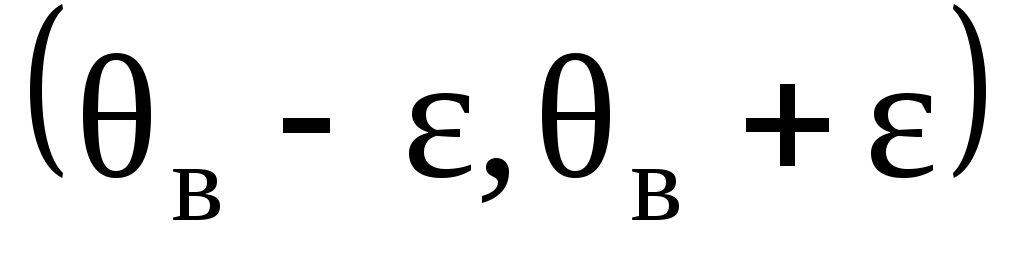– доверительный интервал.

Такие оценки называются интервальными. Например, если распределение X является нормальным с неизвестным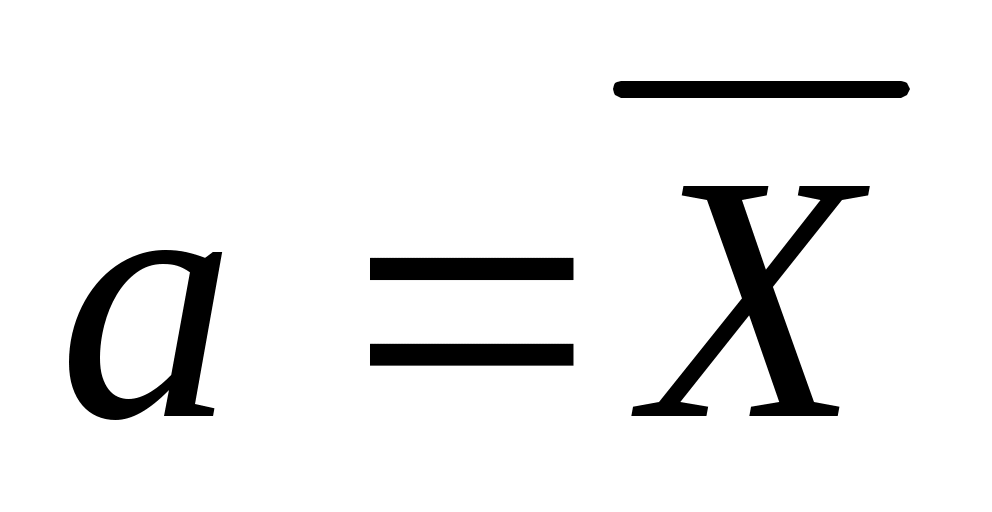 и известным 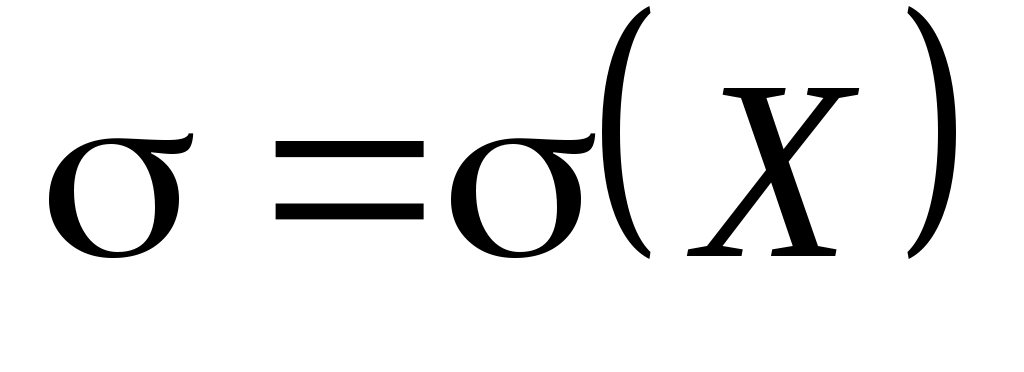параметрами, то радиус интервала 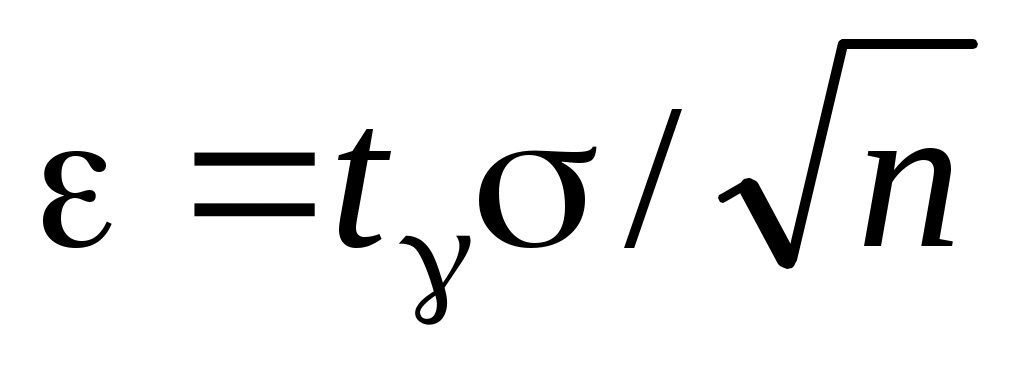, где 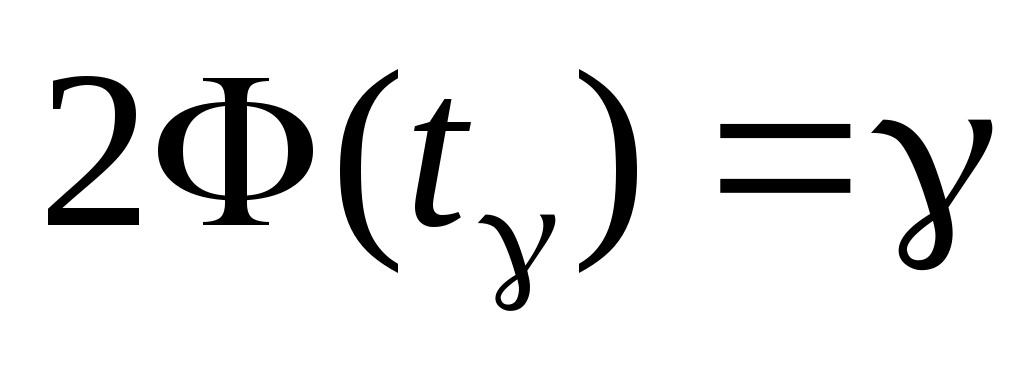, и доверительный интервал для a с надежностью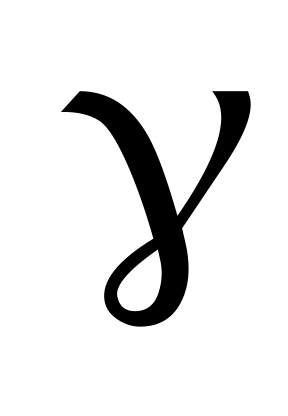

.

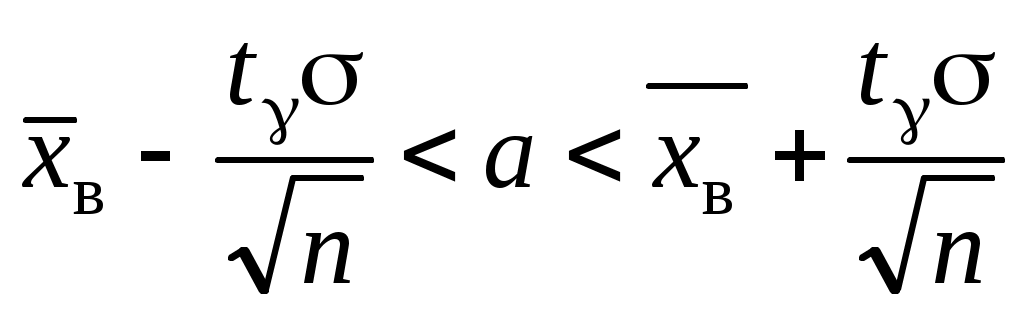Если вместо значения , которое может быть неизвестно, использовать точечную оценку , то получим приближенную интервальную оценку с 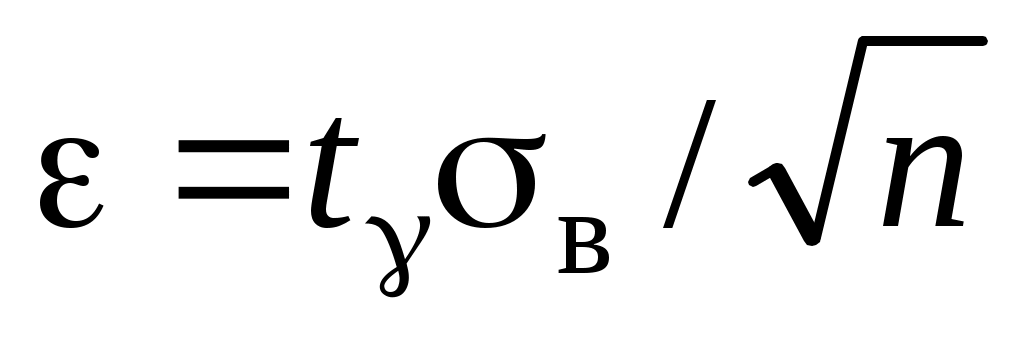, которая по ЦПТ может применяться и для любого X.

Вероятность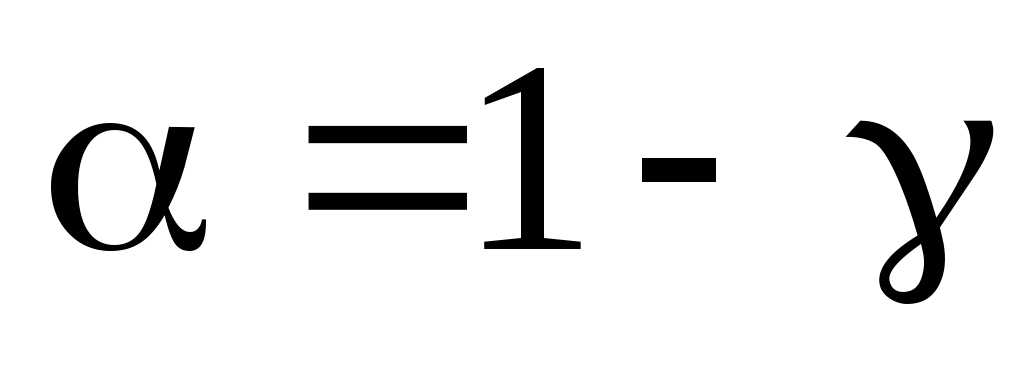 задает вероятность ошибки, т.е. того, что значение a не попадает в доверительный интервал.

Отметим, что имеются и другие виды интервальных оценок для этих и других параметров распределения [1, 2].

В случае равноотстоящих друг от друга значений x_i (например, для сгруппированного вариационного ряда) можно упростить вычисления выборочных характеристик, если, выбрав значение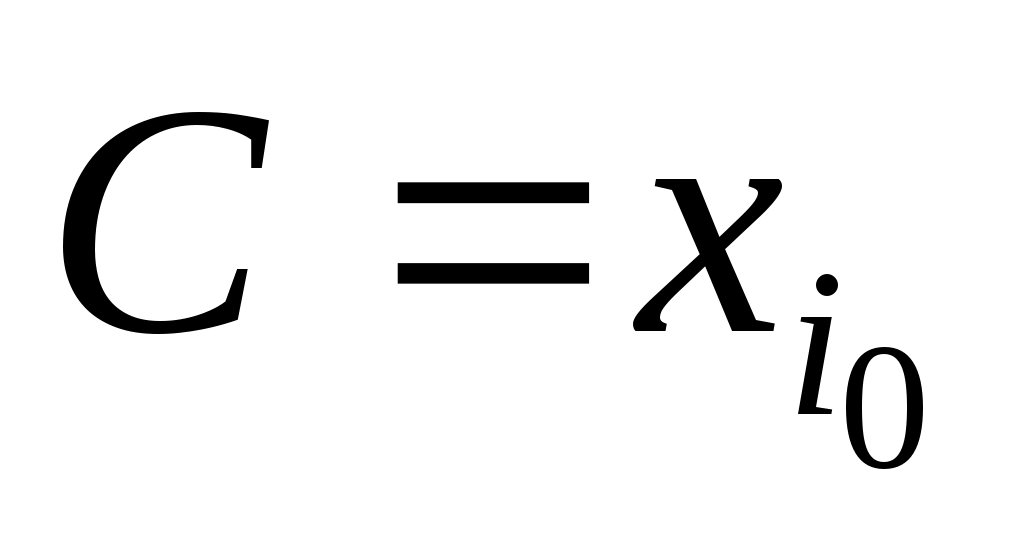 (поближе к середине ряда и с большей частотой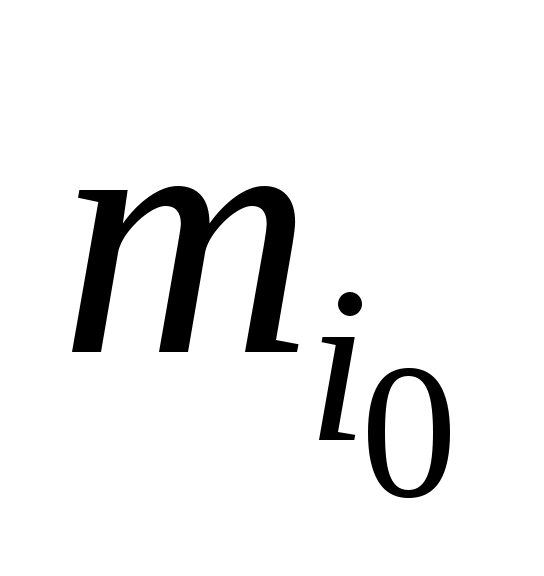

---

), называемое «ложным» нулем, и определив величину шага h для значений ряда, ввести условную варианту по формуле:

.

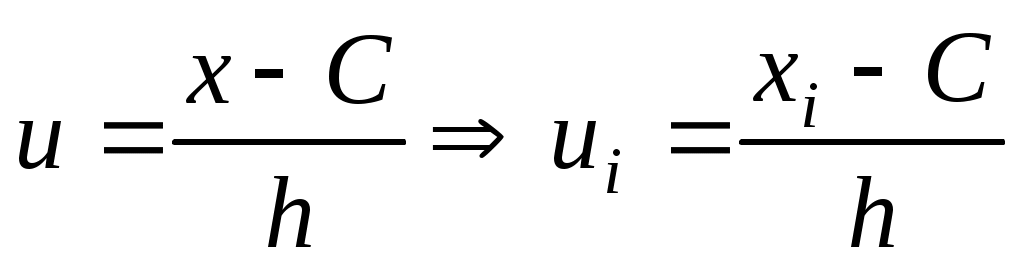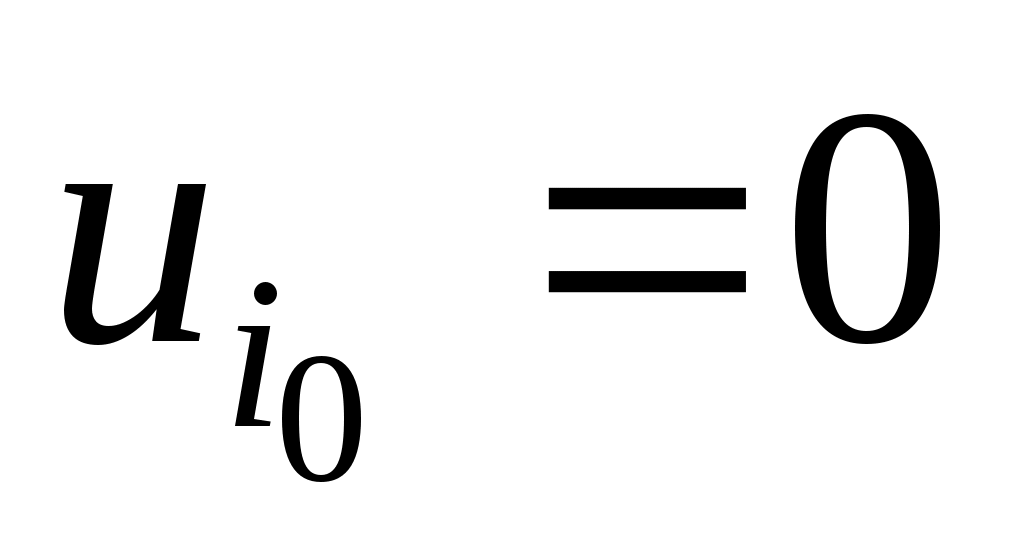Тогда значения условной варианты будут целыми числами, причем, большой частоте будет отвечать , и поэтому выборочные характеристики для условной варианты вычисляются проще:

; ;

; .

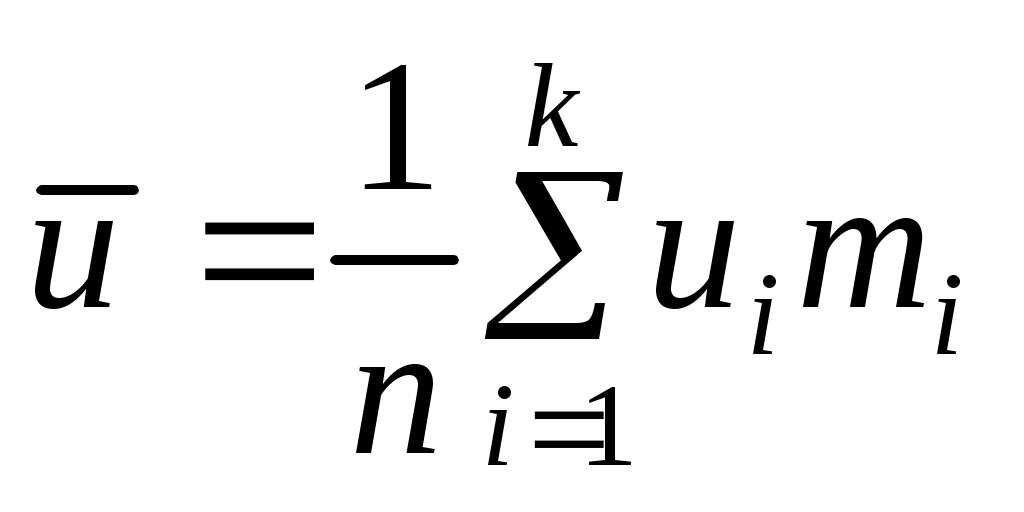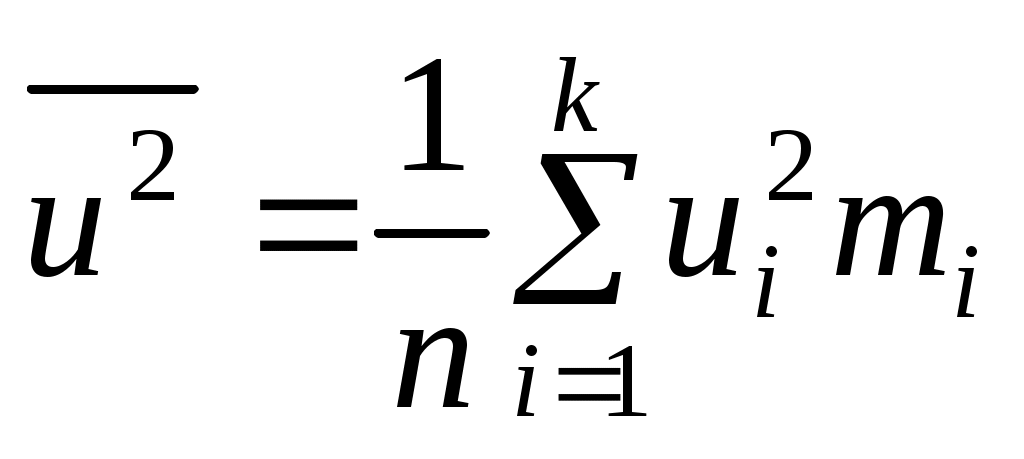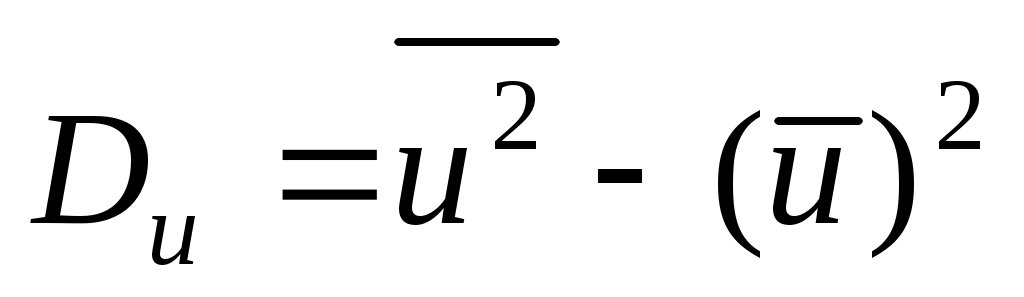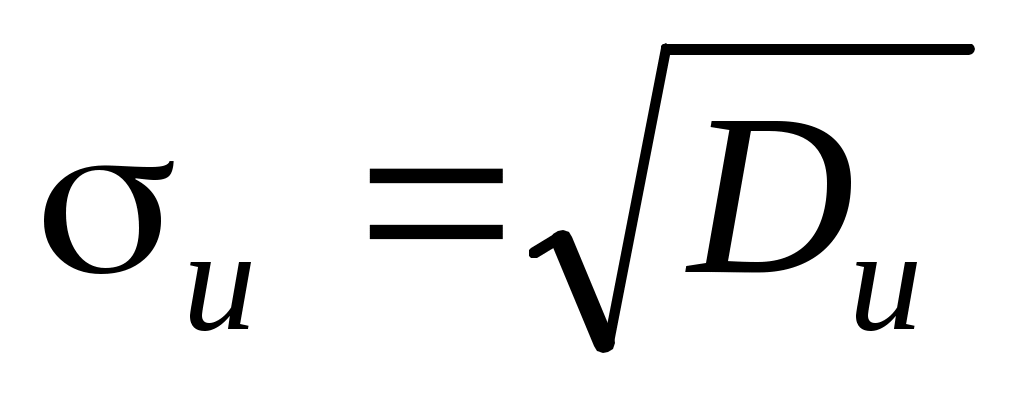Обратный пересчет производится по формулам

, , .

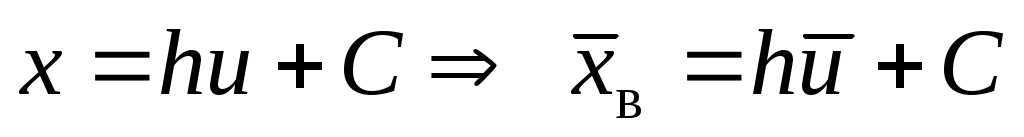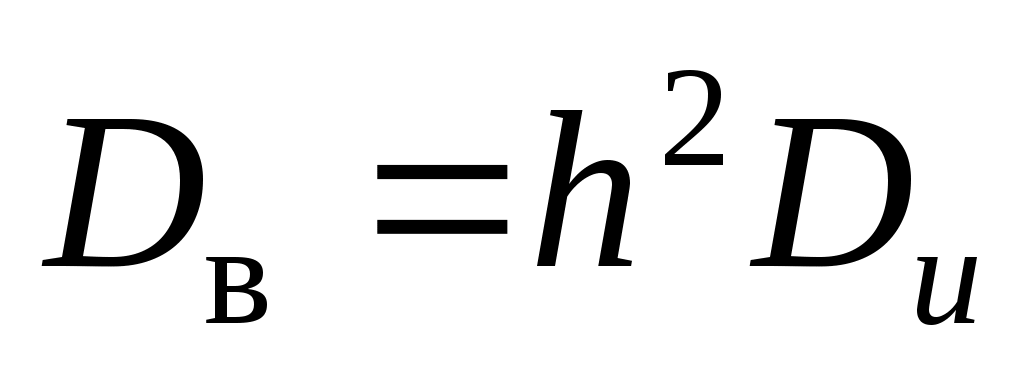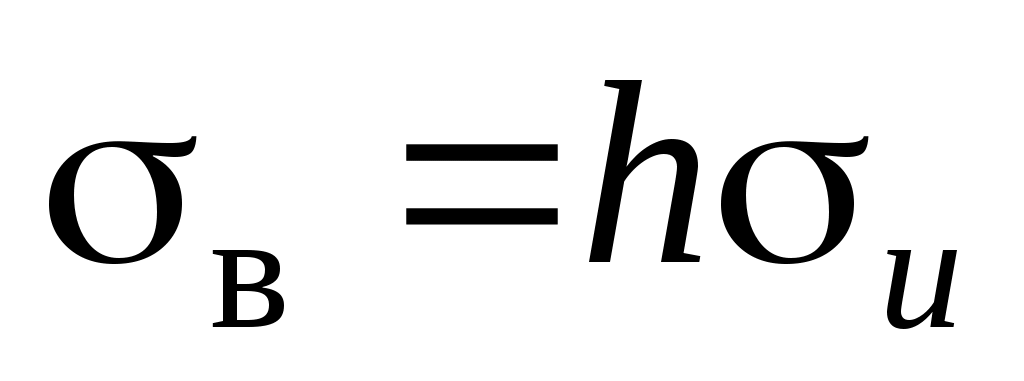При изучении СВ возникает вопрос о возможном виде ее распределения, т.е. о соответствии (согласии) выборочных данных некоторому гипотетическому теоретическому распределению, что является одной из важных задач проверки статистических гипотез.

Основное предположение называется нулевой гипотезой H₀. Возможно рассмотрение и противоположной (альтернативной) гипотезы или каких-нибудь других гипотез. В нашем случае проверка гипотезы H₀ состоит в том, что эмпирические данные получены для нормально распределенной генеральной совокупности. Следовательно, при альтернативной гипотезе эмпирические данные не согласуются с ожидаемым нормальным распределением.

Проверка статистических гипотез осуществляется с помощью статистических критериев. Критерий – случайная величина, значение которой вычисляется по эмпирическим данным, т.е. по выборке. Статистический критерий определяет критическую область, при попадании в которую выборочного значения критерия нулевая гипотеза отвергается. Отвергая нулевую гипотезу (если она на самом деле верна), совершают ошибку первого рода; не отвергая нулевую гипотезу (если она на самом деле неверна), допускают ошибку второго рода. Критическая область определяется так, чтобы вероятность ошибки первого рода не превышала уровня значимости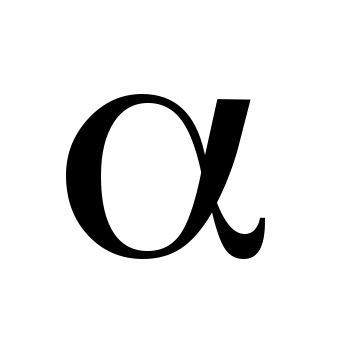 , а вероятность совершить ошибку второго рода была бы наименьшей. Обычно в качестве 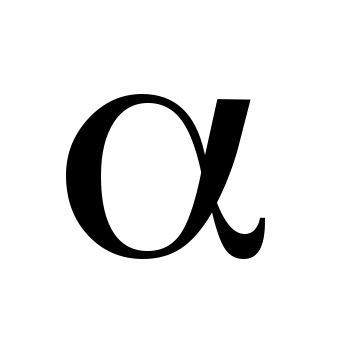берут маленькое число (0,05; 0,01; 0,001; …), при этом следует учитывать, что при будет

---

уменьшаться критическая область, т.е. практически все гипотезы будут приниматься.

Рассмотрим достаточно простой и эффективный критерий согласия – критерий Пирсона хи-квадрат (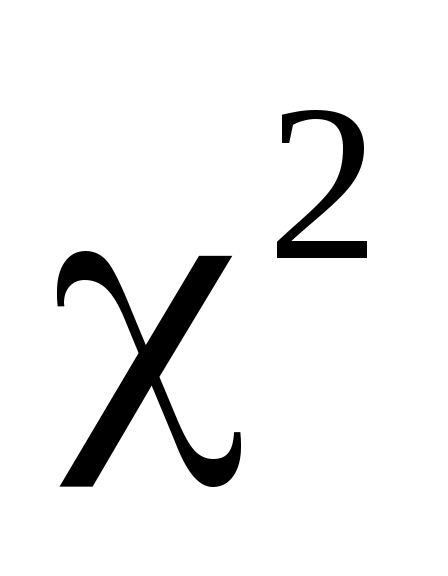 ), для которого мерой расхождения между эмпирическим распределением (выборкой) и теоретическим распределением является разность между эмпирическими и теоретическими частотами для одного и того же значения дискретной случайной величины или, соответственно, для одного и того же интервала в случае непрерывной случайной величины. Для критерия Пирсона находят величину

,

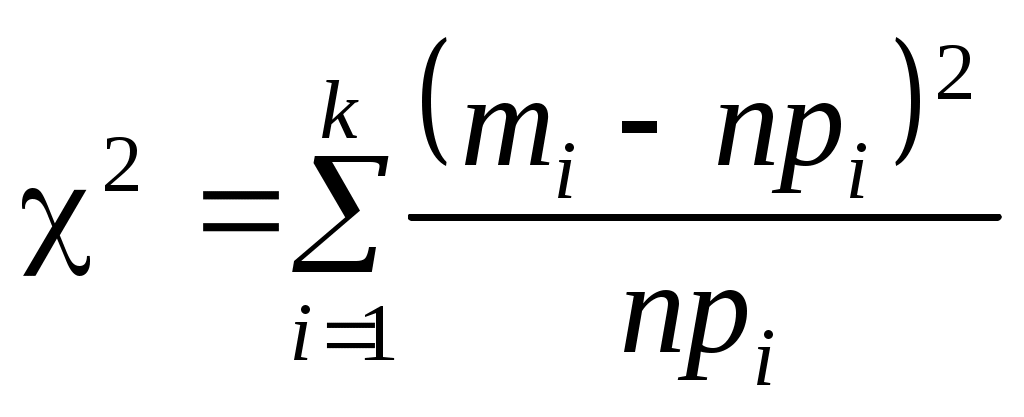где m_i – эмпирическая частота; p_i – соответствующая вероятность для теоретического распределения; np_i– теоретическая частота;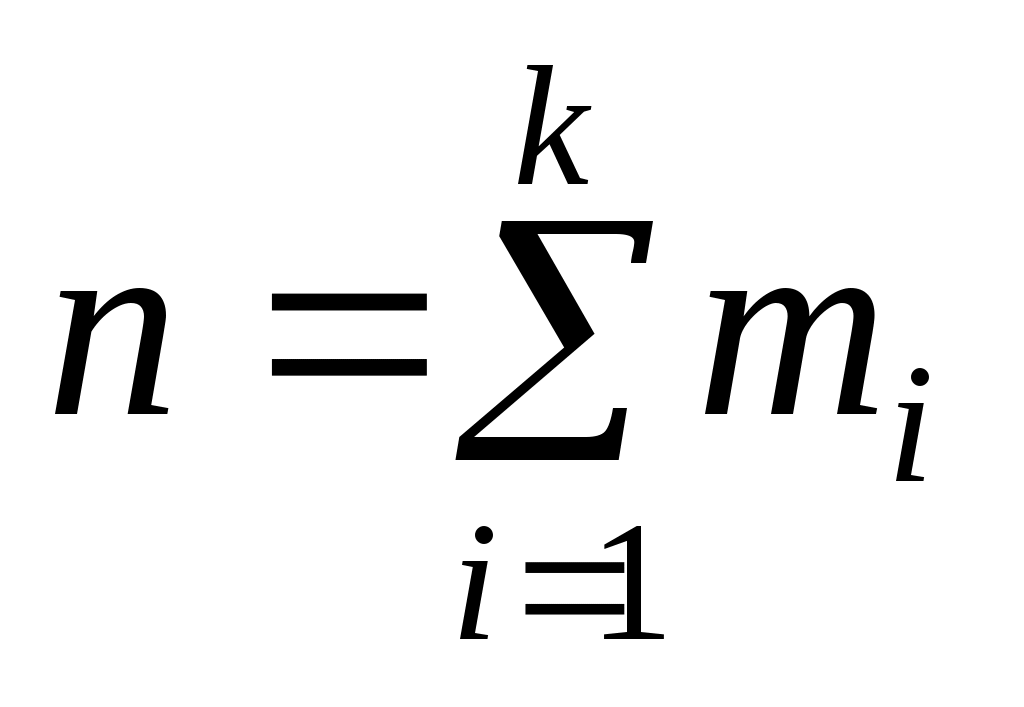 – объем выборки.

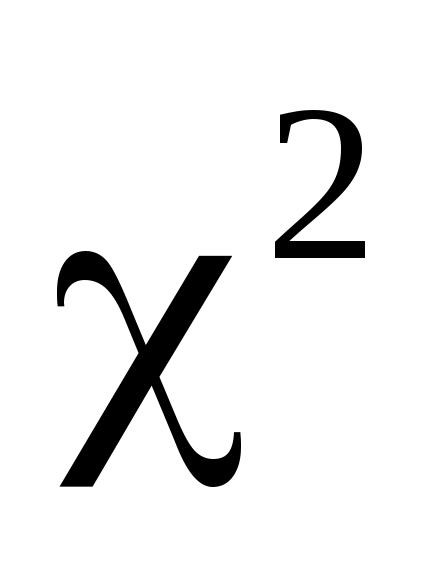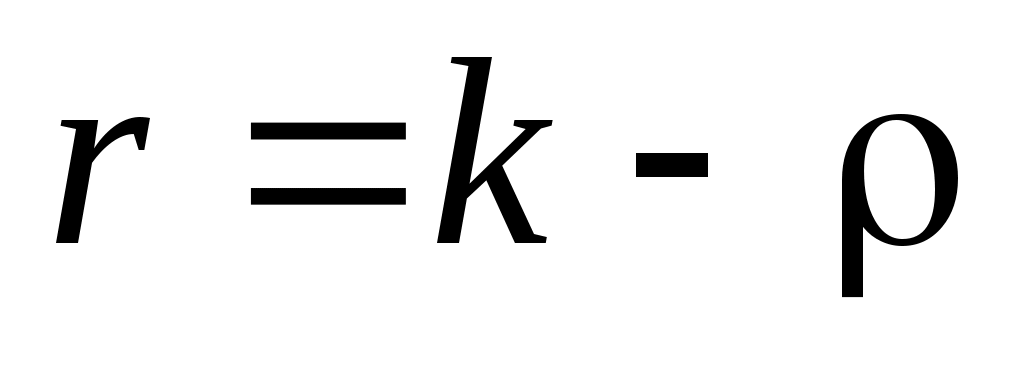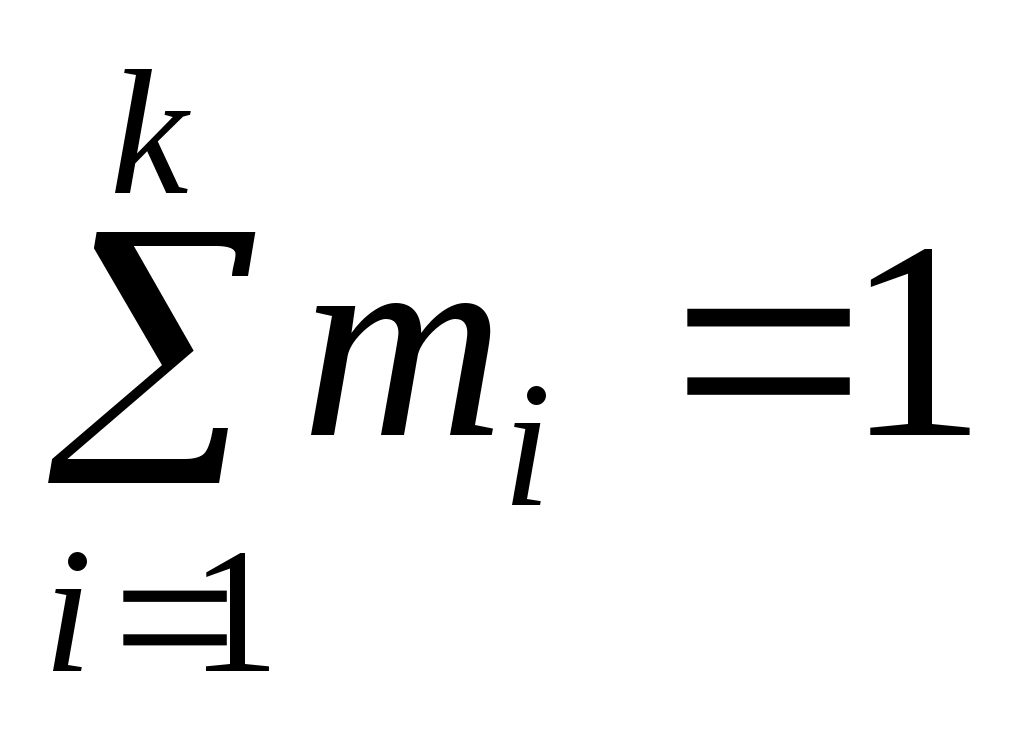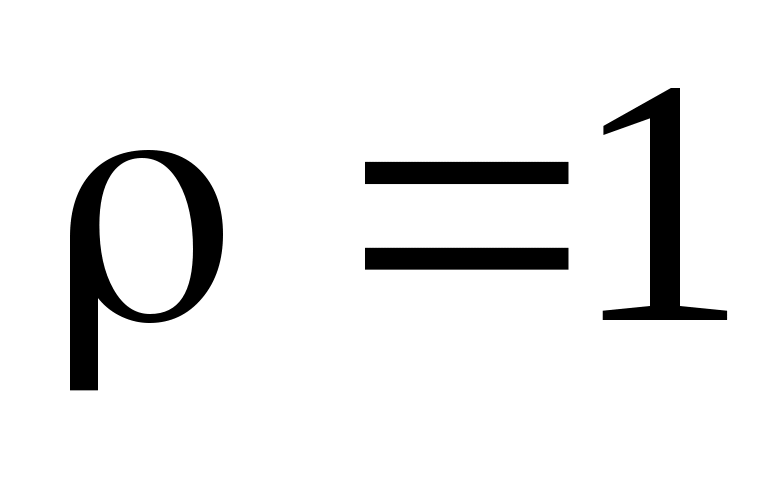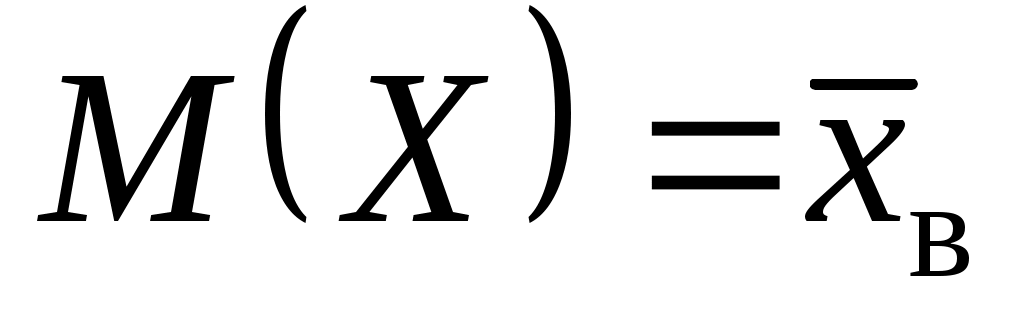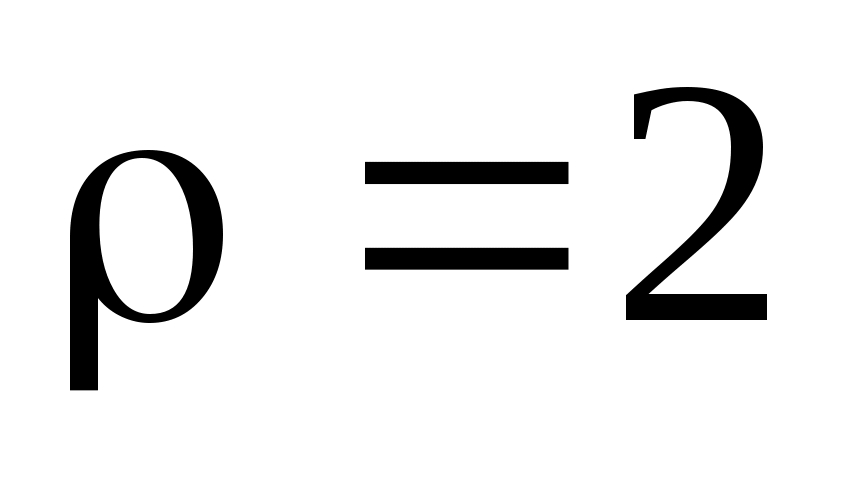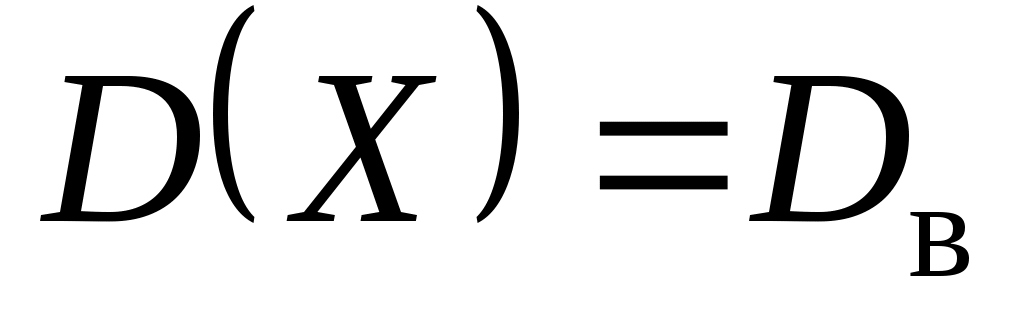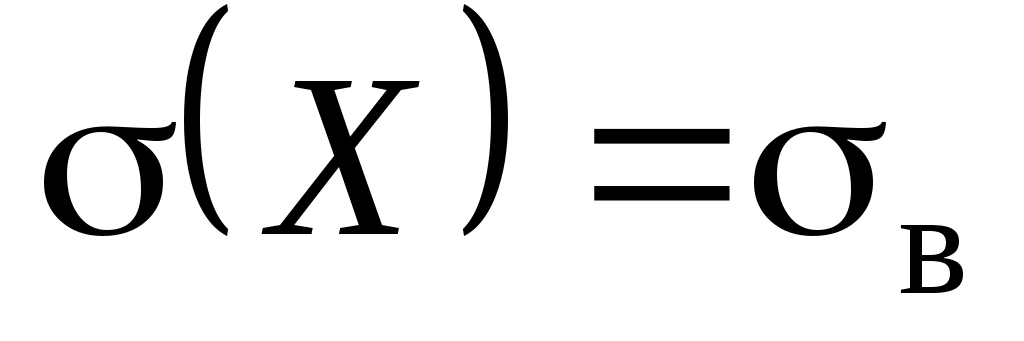Распределение критерия зависит от числа степеней свободы r и уровня значимости  . Число r определяется числом значений (или интервалов) k и числом наложенных связей , равным числу соотношений для выборочных данных и теоретических параметров: . Например, так как всегда , то ; если дополнительно положим , то ; если еще положим и (т.е. ), то 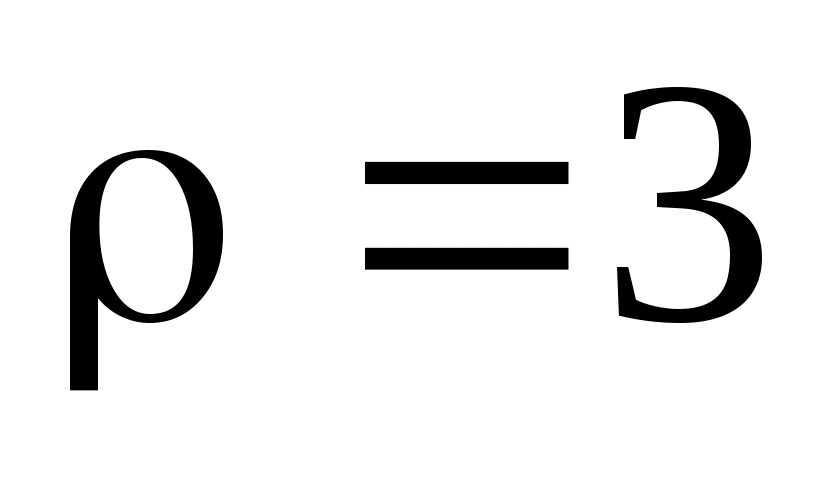и т.д. По специальной таблице [2, 3], зная значения r и

---