Файл: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически.docx

Скачать файл (0,17Мб)

Заказать решение

ВУЗ: Не указан

Категория: Реферат

Дисциплина: Не указана

Добавлен: 07.12.2023

Просмотров: 118

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Производные элементарных функций

Поиск производной по определению в большинстве случаев достаточно трудоемок. На практике для нахождения производных функций используются правила дифференцирования, производные элементарных функций (вывод части формул был приведен выше) и способы вычисления производных.

Перечислим производные элементарных функций, которые являются основой для нахождения производных сложных функций.

1. ^^x^^^^^^^x^¹,

^^a^x^^^^a^x^ln^a,

^^ex^^^ex.

  0 .
a 0;

log _a

x^ ¹log e,

_xa
a 0,
a 1;

ln

x^ ¹.

x

sin x^ cos x.
cos x^ sin x.

6. ^tg x^^

1 _.

cos² x

7. ctg x^ 

1 _.

sin ² x

^^arcsin^x^^^¹.
^^arccos^x^^^^¹.

arctg x^

1 _.

1 x²

arcctg x^ 

1 _.

1 x²

1 2 3 4 5 6 7 8 9

ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ, ФУНКЦИИ, ЗАДАННОЙ НЕЯВНО И ПАРАМЕТРИЧЕСКИ

Производная сложной функции.
Производная неявной функции.
Логарифмическая производная.
Производная функции, заданной параметрически.

Если

Производная сложной функции

Теорема

y

ft

^{сложная}^{функция}⁽t ^–^{независимая}^{переменная,}^^–

промежуточный аргумент);

²⁾f^x₀ ^и

то

^t₀^,^г^де

x₀ t₀^,

Доказательство

ft^

tt₀

^^f^^^x₀^^^^^^t₀^.

^{Рассмотрим}t₀  t

 x t₀  t t₀ ^.

^^x

y

fx₀  x fx₀ ^.

Рассмотрим

y_y_x_.

Пусть

t

t 0 .

x t

Но, так как  lim

x _

x 0 .

t0 __t

При этом
 lim

y _

x0 __x

 lim

y_

lim

^^y lim

x_

f^x

 ^t

  ft

^^^^,

t0 __t

x0 __x

__t_₀__t0 0 0

что и требовалось доказать.

Замечание

В приведенном доказательстве независимая переменная обозначалась ^{символом}t^,^{промежуточная}^{переменная}^–^{символом}x^.^Чаще^{встречается}

y fu^,^u^^^^x^^.^Тогда

y^ fx^ f^u u'x.

Пример

y e^arctg^x, ^y^'– ?

Решение

y  e^u, ^u^^arctg^x.

y^ e^u u

'  e^arctg ^x¹.

1  x²

Дифференциалсложнойфункции

y fx^,^u^^^^x^^,

y^_x

f_u^ u^_x^.

dy

f_u^ u^_xdx

f_u^du^.

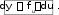
Сравним с формулой
Вывод

dy

f'xdx^.

Дифференциал функции равен произведению производной функции на дифференциал аргумента, при этом не важно, является этот аргумент промежуточным или независимой переменной – инвариантностьформы первого дифференциала.

Смотрите также файлы

Эссе по психологии.docx

Интерактивные методы обучения на уроках истории.docx

Рекомендованные фразы и выражения для написания дневника пп в поликлиники.docx

Контрольная работа по дисциплине Методы принятия управленческих решений Темы.docx

Вопросы экзаменационных билетов.doc

Файл: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически.docx

Производные элементарных функций

ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ, ФУНКЦИИ, ЗАДАННОЙ НЕЯВНО И ПАРАМЕТРИЧЕСКИ

Производная сложной функции

Смотрите также файлы

Информация

Списки файлов

Дополнительно