Файл: Положение о равномерном распределении молекул в пространстве и равномерном распределении их скоростей по всем направлениям называют.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 106
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
— модуль вектора скорости, 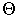 — полярный и
— полярный и 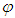 — азимутальный углы, характеризующие направление вектора
— азимутальный углы, характеризующие направление вектора  . При этом элемент объема в пространстве скоростей имеет вид
. При этом элемент объема в пространстве скоростей имеет вид
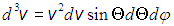 .
.
Для сокращения записи удобно также, кроме вектора , ввести его приращение
, ввести его приращение 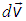 :
:
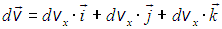 .
.
Здесь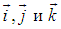 , как обычно, орты декартовых осей
, как обычно, орты декартовых осей 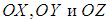 . Соответствующее выражение в сферических координатах мы не выписываем.
. Соответствующее выражение в сферических координатах мы не выписываем.
Тогда, поставленный выше вопрос можно сформулировать и так: «какова вероятность следующего события»: вектор скорости принадлежит (векторному) интервалу от
принадлежит (векторному) интервалу от  до
до 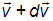
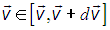 .
.
Последнее выражение можно было бы написать и сразу, однако векторы не образуют упорядоченного множества: неправомерен вопрос, какой вектор больше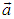 или
или 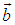 , поэтому и приведены выше разъяснения того, что имеется ввиду под принадлежностью вектора некоторому (векторному) интервалу. Векторный интервал определяет объем в соответствующем пространстве, внутри которого лежит конец вектора, а сам вектор — положение этого объема.
, поэтому и приведены выше разъяснения того, что имеется ввиду под принадлежностью вектора некоторому (векторному) интервалу. Векторный интервал определяет объем в соответствующем пространстве, внутри которого лежит конец вектора, а сам вектор — положение этого объема.
Различия в словах и обозначениях не меняют сути дела, но весьма удобны. Ничто не меняется при переходе от бесконечно малого объема (интервала
(интервала  ) к конечному объему
) к конечному объему 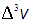 (интервалу
(интервалу 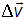 ).
).
Если DN — число молекул, имеющих при заданном состоянии системы вектор скорости в интервале от до
до 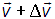 , то это число, в общем случае, вообще говоря, зависит от:
, то это число, в общем случае, вообще говоря, зависит от:
Таким образом,
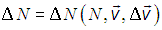
Однако, выше было заявлено и обосновано, что в состоянии термодинамического равновесия распределение молекул по направлениям движения изотропное. На «языке» функции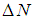 это означает, что она может зависеть только от модуля вектора скорости и не может зависеть от его направления.
это означает, что она может зависеть только от модуля вектора скорости и не может зависеть от его направления.
Следовательно, во-первых,
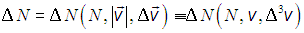
Во- вторых, естественно предположить, что при достаточно малых величинах объема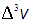
, число молекул в нём (число молекул с вектором скорости, принадлежащем этому объёму) будет пропорционально его величине, то есть
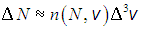
Можно показать, что при стремлении объема в пространстве скоростей к нулю, написанное выше приближенное равенство переходит в точное. Введенная выше функция
к нулю, написанное выше приближенное равенство переходит в точное. Введенная выше функция 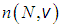 имеет простой смысл: это концентрация частиц в пространстве скоростей
имеет простой смысл: это концентрация частиц в пространстве скоростей
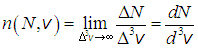
В-третьих, представляется очевидным, что чем больше частиц в системе, тем «при прочих равных» будет больше частиц и в объеме и их концентрация
и их концентрация 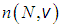 . Поэтому естественно от концентрации частиц перейти к удельной величине не зависящей от полного числа частиц в системе
. Поэтому естественно от концентрации частиц перейти к удельной величине не зависящей от полного числа частиц в системе
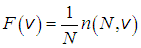
Эта функция зависит только от скорости и дает относительное количество (долю) молекул, имеющих скорость в единичном объеме в пространстве скоростей вблизи скорости с модулем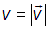 .Эта функция
.Эта функция 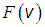 называется функцией распределения молекул для вектора скорости. Если взять несколько порций одного и того же газа, находящихся в идентичных условиях (одинаковы р и Т), то распределение молекул по скоростям в них также будет идентично. Зная вид
называется функцией распределения молекул для вектора скорости. Если взять несколько порций одного и того же газа, находящихся в идентичных условиях (одинаковы р и Т), то распределение молекул по скоростям в них также будет идентично. Зная вид 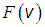 ,можно найти количество молекул dN из общего числа молекул N, проекции вектора скорости которых одновременно принадлежат интервалам
,можно найти количество молекул dN из общего числа молекул N, проекции вектора скорости которых одновременно принадлежат интервалам
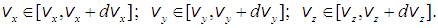
Это число равно
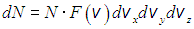 ,
,
или, при использовании сферических координат в пространстве скоростей,
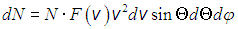
Подчеркнем, что это распределение вероятностей для вектора скорости, то есть сразу для трех величин: либо для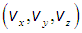 либо для
либо для 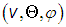 , в зависимости от используемой в пространстве скоростей системы координат.
, в зависимости от используемой в пространстве скоростей системы координат.
Концентрация частиц в пространстве скоростей должна подчиняться условию, имеющему простой физический смысл: число молекул со всевозможными векторами скорости, которым соответствуют все возможные объемы , на которые можно разбить всё пространство скоростей, должно быть равно полному числу частиц в системе. При переходе к пределу, то есть от
, на которые можно разбить всё пространство скоростей, должно быть равно полному числу частиц в системе. При переходе к пределу, то есть от  к
к  , суммирование превращается в интегрирование по всему пространству скоростей и мы имеем:
, суммирование превращается в интегрирование по всему пространству скоростей и мы имеем:
откуда следует условие нормировки функции распределения
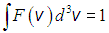 .
.
Вычисление, написанного выше, нормировочного интеграла разумеется возможно при использовании любой системы координат в пространстве скоростей. Например, в декартовой системе
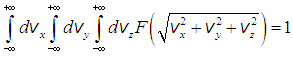 .
.
Однако, «грех» не воспользоваться фактом изотропности распределения молекул по направлениям движения, отражением которого является зависимость функции распределения
 только от модуля вектора скорости. В сферических координатах нормировочный интеграл имеет существенно проще, так как два из трех интегрирований можно провести в общем виде:
только от модуля вектора скорости. В сферических координатах нормировочный интеграл имеет существенно проще, так как два из трех интегрирований можно провести в общем виде:
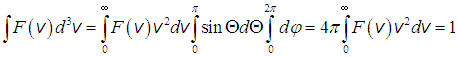
Функция распределения для газов была найдена теоретически Максвеллом (1859) и носит его имя. Далее мы установим ее вид.
Распределение Максвелла. Поскольку все направления движения молекул в пространстве равноправны, распределение скоростей должно быть изотропным и функция распределения n(v) не может зависеть от направления скорости. Это означает, что n(v) не может быть произвольной функцией от компонент скорости vх, vy, vz, а должна зависеть лишь от абсолютной величины скорости
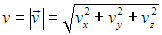
В зависимости от выбранной системы координат вероятность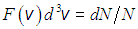 имеет различный вид.
имеет различный вид.
В декартовой системе
В цилиндрической системе
В сферической системе
Далее предлагается простой, хотя и не вполне строгий вывод вида функции распределения. Рассмотрим процесс столкновения двух частиц, движущихся со скоростями v1 и v2. Пусть в результате соударения скорости молекул изменяются и превращаются в
Для сокращения записи удобно также, кроме вектора
Здесь
Тогда, поставленный выше вопрос можно сформулировать и так: «какова вероятность следующего события»: вектор скорости
Последнее выражение можно было бы написать и сразу, однако векторы не образуют упорядоченного множества: неправомерен вопрос, какой вектор больше
Различия в словах и обозначениях не меняют сути дела, но весьма удобны. Ничто не меняется при переходе от бесконечно малого объема
Если DN — число молекул, имеющих при заданном состоянии системы вектор скорости в интервале от
-
общего числа молекул N в системе; -
величины объема в пространстве скоростей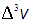 (интервала
(интервала 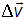 );
); -
самого вектора скорости (так как при одинаковых по величине элементах объема, но при разных его положениях в пространстве скоростей, в общем случае, число частиц будет различным).
(так как при одинаковых по величине элементах объема, но при разных его положениях в пространстве скоростей, в общем случае, число частиц будет различным).
Таким образом,
Однако, выше было заявлено и обосновано, что в состоянии термодинамического равновесия распределение молекул по направлениям движения изотропное. На «языке» функции
Следовательно, во-первых,
Во- вторых, естественно предположить, что при достаточно малых величинах объема
, число молекул в нём (число молекул с вектором скорости, принадлежащем этому объёму) будет пропорционально его величине, то есть
Можно показать, что при стремлении объема в пространстве скоростей
В-третьих, представляется очевидным, что чем больше частиц в системе, тем «при прочих равных» будет больше частиц и в объеме
Эта функция зависит только от скорости и дает относительное количество (долю) молекул, имеющих скорость в единичном объеме в пространстве скоростей вблизи скорости с модулем
Это число равно
или, при использовании сферических координат в пространстве скоростей,
Подчеркнем, что это распределение вероятностей для вектора скорости, то есть сразу для трех величин: либо для
Концентрация частиц в пространстве скоростей должна подчиняться условию, имеющему простой физический смысл: число молекул со всевозможными векторами скорости, которым соответствуют все возможные объемы
| | | (3.10) |
откуда следует условие нормировки функции распределения
Вычисление, написанного выше, нормировочного интеграла разумеется возможно при использовании любой системы координат в пространстве скоростей. Например, в декартовой системе
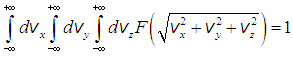 .
.Однако, «грех» не воспользоваться фактом изотропности распределения молекул по направлениям движения, отражением которого является зависимость функции распределения
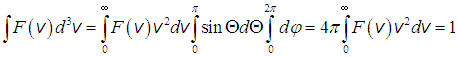
Функция распределения для газов была найдена теоретически Максвеллом (1859) и носит его имя. Далее мы установим ее вид.
Распределение Максвелла. Поскольку все направления движения молекул в пространстве равноправны, распределение скоростей должно быть изотропным и функция распределения n(v) не может зависеть от направления скорости. Это означает, что n(v) не может быть произвольной функцией от компонент скорости vх, vy, vz, а должна зависеть лишь от абсолютной величины скорости
В зависимости от выбранной системы координат вероятность
В декартовой системе
| | | (3.11) |
В цилиндрической системе
| | | (3.12) |
В сферической системе
| | | (3.13) |
Далее предлагается простой, хотя и не вполне строгий вывод вида функции распределения. Рассмотрим процесс столкновения двух частиц, движущихся со скоростями v1 и v2. Пусть в результате соударения скорости молекул изменяются и превращаются в