Файл: Учебнометодическое пособие по дисциплине физика часть 1 Физические основы механики. Электричество. Электромагнетизм. Для студентов 1 курса.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 533
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
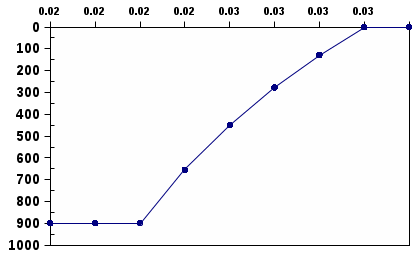
Таблица 2
| r, м | 0 | 0,010 | 0,020 | 0,022 | 0,024 | 0,026 | 0,028 | 0,030 | 0,04 |
| (r), В | 899 | 899 | 899 | 654 | 450 | 277 | 128 | 0 | 0 |
По данным таблицы построим график = (r) (рис. 10).
ммммммм
r,м
Рис. 10
П р и м е р 6. Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью
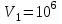 м/с, чтобы скорость его возросла в n = 2 раза.
м/с, чтобы скорость его возросла в n = 2 раза.Р е ш е н и е. Ускоряющую разность потенциалов можно найти, вычислив работу А сил электростатического поля. Эта работа определяется произведением заряда электрона е на разность потенциалов U
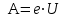 . (1)
. (1)Работа сил электростатического поля в данном случае равна изменению кинетической энергии электрона
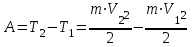 , (2)
, (2)где
 и
и  - кинетические энергии электрона до и после прохождения ускоряющего поля; m- масса электрона;
- кинетические энергии электрона до и после прохождения ускоряющего поля; m- масса электрона;  и
и  - начальная и конечная его скорости.
- начальная и конечная его скорости.Приравняв правые части равенств (1) и (2), получим

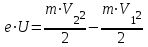
или
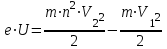 ,
,где
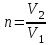 .
.Отсюда искомая разность потенциалов
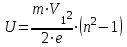 . (3)
. (3)
Подставим числовые значения физических величин и выполним вычисления
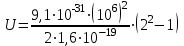 В = 8,53 В.
В = 8,53 В.П р и м е р 7. Конденсатор емкостью
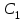 = 3 мкФ был заряжен до разности потенциалов
= 3 мкФ был заряжен до разности потенциалов  = 40 В. После отключения от источника тока конденсатор был соединен параллельно с другим незаряженным конденсатором емкостью
= 40 В. После отключения от источника тока конденсатор был соединен параллельно с другим незаряженным конденсатором емкостью 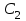 = 5мкФ. Какая энергия W′ израсходуется на образование искры в момент присоединения второго конденсатора?
= 5мкФ. Какая энергия W′ израсходуется на образование искры в момент присоединения второго конденсатора?Дано:
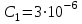 Ф;
Ф; 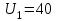 В;
В; 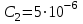 Ф.
Ф.Найти: W′.
Р е ш е н и е. Энергия W′, израсходованная на образование икры,
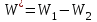 , (1)
, (1)где
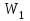 - энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора;
- энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора;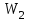 - энергия, которую имеет батарея, составленная из первого и второго конденсаторов.
- энергия, которую имеет батарея, составленная из первого и второго конденсаторов.Энергия заряженного конденсатора определяется по формуле
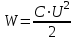 , (2)
, (2)где С – емкость конденсатора или батареи конденсаторов; U – разность потенциалов на обкладках конденсаторов.
Выразив в формуле (1) энергии
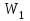 и
и 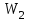 по формуле (2) и принимая во внимание, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим:
по формуле (2) и принимая во внимание, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим: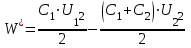 , (3)
, (3)где
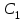 и
и 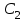 - емкости первого и второго конденсаторов;
- емкости первого и второго конденсаторов; - разность потенциалов, до которой был заряжен первый конденсатор;
- разность потенциалов, до которой был заряжен первый конденсатор; - разность потенциалов на зажимах батареи конденсаторов.
- разность потенциалов на зажимах батареи конденсаторов.
Учитывая, что заряд после присоединения второго конденсатора остался прежний, выразим разность потенциалов
 следующим образом:
следующим образом: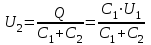 .
.Подставив выражение
 в формулу (3), получим
в формулу (3), получим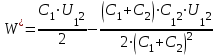 .
. После простых преобразований найдем
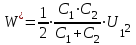 .
.В полученное выражение подставим числовые значения и вычислим W′:
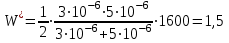 мДж.
мДж.П р и м е р 8. Потенциометр с сопротивлением r = 100 Ом подключен к батарее, Э
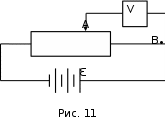 ДС которой ε = 150 В и внутреннее сопротивление
ДС которой ε = 150 В и внутреннее сопротивление 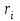 =50 Ом (Рис. 11). Определить показания вольтметра с сопротивлением
=50 Ом (Рис. 11). Определить показания вольтметра с сопротивлением 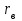 = 500 Ом, соединенного с одной из клемм потенциометра и подвижным контактом, установленным посередине потенциометра. Какова разность потенциалов между теми же точками потенциометра при отключенном вольтметре?
= 500 Ом, соединенного с одной из клемм потенциометра и подвижным контактом, установленным посередине потенциометра. Какова разность потенциалов между теми же точками потенциометра при отключенном вольтметре?Р е ш е н и е. Показание
 вольтметра, подключенного к точкам А и В (рис.11), определяется по формуле:
вольтметра, подключенного к точкам А и В (рис.11), определяется по формуле: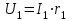 , (1)
, (1)где
 - сила тока в неразветвленной части цепи;
- сила тока в неразветвленной части цепи; - сопротивление параллельно соединенных вольтметра и половины потенциометра.
- сопротивление параллельно соединенных вольтметра и половины потенциометра.Силу тока
 найдем по закону Ома для всей цепи:
найдем по закону Ома для всей цепи: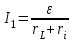 , (2)
, (2)где
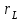 - сопротивление внешней цепи.
- сопротивление внешней цепи.Внешнее сопротивление
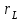 есть сумма двух сопротивлений:
есть сумма двух сопротивлений: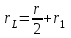
. (3)
Сопротивление
 параллельного соединения может быть найдено по формуле:
параллельного соединения может быть найдено по формуле: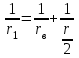 ,
,откуда
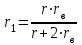 .
.Подставив числовые значения, найдем
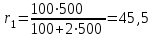 Ом.
Ом.Подставив в выражение (2) правую часть равенства (3), определим силу тока
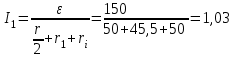 А.
А.Если подставить значение
 и
и  в формулу (1), то можно определить показание вольтметра
в формулу (1), то можно определить показание вольтметра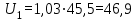 В.
В.Разность потенциалов между точками А и В при отключенном вольтметре равна произведению силы тока
 на половину сопротивления потенциометра, т. е.
на половину сопротивления потенциометра, т. е.  или
или 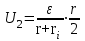 .
.Подставляя сюда числовые значения, получим
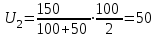 В.
В.П р и м е р 9. ЭДС батареи ε = 12 В. Наибольшая сила тока, которую может дать батарея,
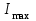 = 6 А. Определить максимальную мощность
= 6 А. Определить максимальную мощность 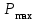 , которая может выделиться во внешней цепи.
, которая может выделиться во внешней цепи.Р е ш е н и е. Воспользуемся законом Ома для полной цепи
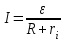 ,
,где ε – ЭДС источника;
R- сопротивление внешней цепи;
 - внутреннее сопротивление источника тока.
- внутреннее сопротивление источника тока.Максимальное значение тока достигается в случае, когда
R = 0; т. е.
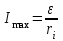 .
.Мощность, выделяемая в цепи, в общем виде определяется формулой
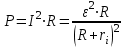 .
.Для того чтобы определить экстремальную мощность, воспользуемся условием
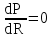 , в результате дифференцирования дробного выражения получим
, в результате дифференцирования дробного выражения получим
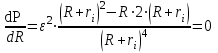 .
.Следовательно, для равенства нулю первой производной достаточно, чтобы
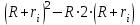 = 0, т. е. экстремальная мощность выделяется в цепи при условии
= 0, т. е. экстремальная мощность выделяется в цепи при условии 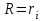 , а максимальная мощность выделяется в цепи при максимальном токе, поэтому можно записать
, а максимальная мощность выделяется в цепи при максимальном токе, поэтому можно записать 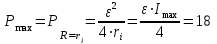 Вт.
Вт.П р и м е р 10. Сила тока в проводнике сопротивлением r = 20 Ом нарастает в течение времени Δt = 2 с по линейному закону от
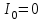 до I = 6 А. Определить теплоту
до I = 6 А. Определить теплоту  , выделившуюся в этом проводнике за первую и
, выделившуюся в этом проводнике за первую и  - за вторую секунды, а также найти отношение
- за вторую секунды, а также найти отношение 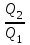 .
.Р е ш е н и е. Закон Джоуля- Ленца в виде
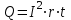 справедлив для случая постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде
справедлив для случая постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде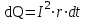 . (1)
. (1)Здесь сила тока I является некоторой функцией времени. В нашем случае
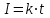 , (2)
, (2)где k- коэффициент пропорциональности, численно равный приращению силы тока в единицу времени, т. е.
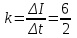 А/с.
А/с.С учетом (2) формула (1) примет вид
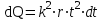 . (3)
. (3)Для определения теплоты, выделившейся за конечный промежуток времени Δt, выражение (3) надо проинтегрировать в пределах от
 до
до 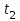
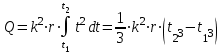 .
.При определении теплоты, выделившейся за первую секунду, пределы интегрирования
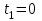 ,
, 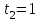 с и, следовательно,
с и, следовательно,