Файл: Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11.docx

вектора неизвестных на (k+1)-й итерации используются , уже вычисленные на (k+1)-й итерации. Значения остальных компонент берутся из предыдущей итерации. Так же как и в методе простых итераций строится эквивалентная СЛАУ :

при ненулевых диагональных элементах 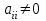, (если какой-либо коэффициент на главной диагонали равен нулю, достаточно соответствующее уравнение поменять местами с любым другим уравнением). Получим следующие выражения для компонентов вектора 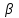и матрицы 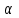эквивалентной системы:

, .

За начальное приближение принимается вектор правых частей 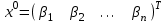. Тогда метод Зейделя для известного вектора 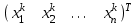на k-ой итерации имеет вид:

.
Пример решения СЛАУ методом Зейделя в MatLab :
1.Создадим М-фаил zeydel.m

function X=zeydel(A,B,X0,delta,Imax)
% Итерация Гаусса – Зейделя.
% A - невырожденная матрица коэффициентов
% размером n x n;
% B - вектор-столбец свободных членов;
% X0 - вектор-столбец начального приближения;
% delta - допустимая относительная погрешность;
% Imax - максимальное число итераций;
% X - приближенное решение линейной системы AX = B.

n=length(B);
err=5*delta;
X=X0;
ct=0;
while err>delta
Xp=X;
for i=1:n
X(i)=(B(i)-A(i,[1:i-1,i+1:n])*…
X([1:i-1,i+1:n]))/A(i,i);
end

if max(abs(X0))==0
error('Следует изменить начальное приближение')
break
end
err=max(abs(X-Xp))/max(abs(X0));
ct=ct+1;
Xe(ct,:)=[X' err];
if ct>Imax
error('Требуемое число итераций слишком велико')

---

break
end
end
Xe
ct

2. Далее в командной строке последовательно набираем команды, приведенные ниже.

A=[ 2 -1 1; 4 -6 1; -2 1 8];
B=[2; -4; 16];
X0=[1; 2; 2];
X=zeydel(A,B,X0,1e-5,1e2)
Первая из них задает матрицу коэффициентов А размером 3 на 3, вторая – вектор-столбец свободных членов В размером 3 на 1, третья – вектор-столбец начального приближения Х0 размером 3 на 1 и четвертая осуществляет запуск итерационного процесса Зейделя с заданными параметрами.
3. Полученные результаты будут представлены на экране монитора в следующем виде:
Xe =
1.0000 1.6667 2.0417 0.1667
0.8125 1.5486 2.0095 0.0937
0.7695 1.5146 2.0031 0.0215
0.7558 1.5044 2.0009 0.0069
0.7517 1.5013 2.0003 0.0020
0.7505 1.5004 2.0001 0.0006
0.7502 1.5001 2.0000 0.0002
0.7500 1.5000 2.0000 0.0001
0.7500 1.5000 2.0000 0.0000
0.7500 1.5000 2.0000 0.0000

ct = 10

X =0.7500 1.5000 2.0000.
Где первые три столбца матрицы Хе представляют собой приближения переменных х1, х2, х3 к решению, четвертый столбец – погрешности приближений,

ct – число итераций, Х – вектор результата.

Таким образом, решение системы (4.34) с относительной погрешностью 10^-5 и с использованием начального приближения х⁽⁰⁾ = [1, 2, 2] методом Гаусса – Зейделя было получено за 10 итераций. Т. е. в данном случае число итераций в процессе Гаусса – Зейделя оказалось в 1,7 раза меньше, чем при решении методом Якоби.
Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания в среде MatLab.

5. Выводы и анализ полученных результатов.
Контрольные вопросы:

1. 
   Суть метода Зейделя?
   
2. 
   В каких случаях возможно решение систем уравнений методом Зейделя?
   
3. 
   С помощью, какой функции в MatLab можно вычислить максимум функции?
   
4. 
   С помощью, какой функции в MatLab можно ввести матрицу?
   
5. 
   Что значит решить СЛАУ?
   
6. 
   Что определяет данная функции length(B)?
   

---

Лабораторная работа №9.

«Численное решение алгебраических проблем собственных значений»

Цель: Изучить методы нахождения собственных значений матрицы.
Задание:

1. 
   Найдите наибольшее по модулю собственное число и соответствующий ему собственный вектор.
   
   1. 
      Степенным методом
      
   2. 
      Методом скалярных произведений
      

(В качестве начального взять вектор [1,1,1,1] или [1,0,0,0])

2. 
   Решить полную проблему собственных значений методом вращения Якоби;
   
3. 
   Используя среду MatLab проверить вычисления;
   

Варианты заданий:

№ варианта	Матрица А

---

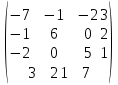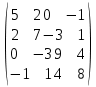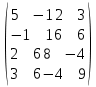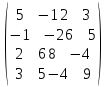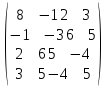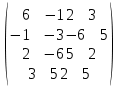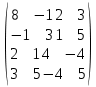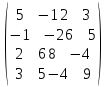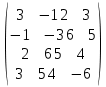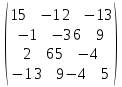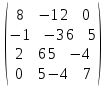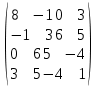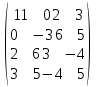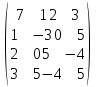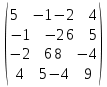Теоретический материал:

Рассмотрим матрицу 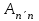в n - мерном вещественном пространстве 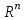векторов

.

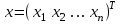1. Собственным вектором 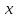матрицы A называется ненулевой вектор, удовлетворяющий равенству

,

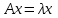где 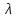- собственное значение матрицы A, соответствующее рассматриваемому собственному вектору.

2. Собственные значения матрицы A с действительными элементами могут быть вещественными различными, вещественными кратными, комплексными попарно сопряженными, комплексными кратными.

Степенной метод:

РМ-алгоритм.

Шаг 1. Ввести 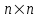-матрицу А, задать 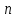-мерный вектор 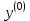, вычислить 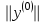и вектор 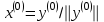; положить .

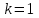Шаг 2. Вычислить вектор .

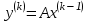Шаг 3. Вычислить 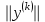и .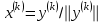

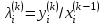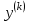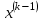Шаг 4.Вычислить отношения (координат векторов и ) при 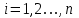таких, что 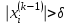, где 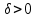- некоторое задаваемое малое число (допуск).

Шаг 5. Подвергнуть числа 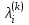тесту на сходимость.

Если обнаруживается совпадение требуемого числа знаков в

---

и 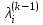( 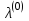можно задавать произвольно), то работу алгоритма прекратить и за старшее собственное число 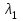принять усредненное (по 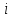) значение , а за нормированный старший собственный вектор 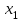-вектор .

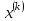В противном случае – вернуться к шагу 2.

Метод скалярных произведений:

SP-алгоритм.

1. 
   Ввести: данную симметричную -матрицу А, произвольный -мерный начальный вектор 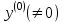, малое число 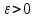(определяющее допустимую абсолютную погрешность искомого собственного числа 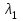), число 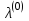для начального сравнения (например, 0). Положить (счетчик итераций).
   
2. 
   Вычислить скаляры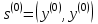 , 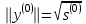и вектор .
   
3. 
   Вычислить (итерация нормированного вектора).
   
4. 
   Вычислить: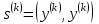 и 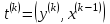(скалярные произведения), 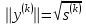, (приближение к нормированному собственному вектору), 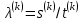(приближение к собственному числу ).
   
5. 
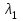   Если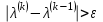 , положить 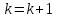и вернуться к шагу 3, иначе завершить работу алгоритма, считая , .
   

---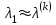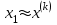