Файл: Лабораторная работа 1. 3 Основы теории погрешностей 3 Лабораторная работа 2. 11 Основы теории погрешностей 11.docx

Метод вращений Якоби

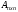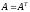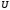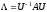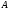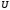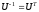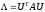Метод вращений Якоби применим только для симметрических матриц ( ) и решает полную проблему собственных значений и собственных векторов таких матриц. Он основан на отыскании с помощью итерационных процедур матрицы в преобразовании подобия , а поскольку для симметрических матриц матрица преобразования подобия является ортогональной ( ), то , где 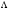- диагональная матрица с собственными значениями на главной диагонали

.
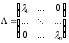Пусть дана симметрическая матрица A. Требуется для нее вычислить с точностью 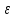все собственные значения и соответствующие им собственные векторы. Алгоритм метода вращения следующий:

Пусть известна матрица 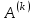на k–й итерации, при этом для k=0 .

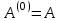1. Выбирается максимальный по модулю недиагональный элемент 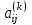матрицы ( = ) .

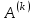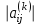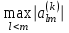2. Ставится задача найти такую ортогональную матрицу 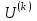, чтобы в результате преобразования подобия 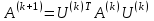произошло обнуление элемента 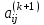матрицы 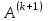. В качестве ортогональной матрицы выбирается матрица вращения, имеющая следующий вид: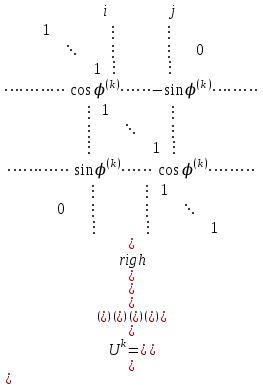

---

,

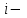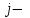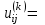
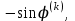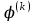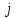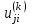
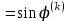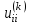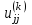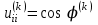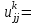
В матрице вращения на пересечении й строки и го столбца находится элемент где - угол вращения, подлежащий определению. Симметрично относительно главной диагонали ( -я строка, -й столбец) расположен элемент ; Диагональные элементы и равны соответственно , 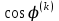; другие диагональные элементы 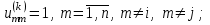остальные элементы в матрице вращения равны нулю.

Угол вращения 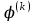определяется из условия :

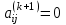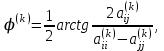причем если 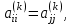то .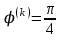

3. Строится матрица



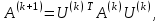
в которой элемент

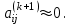
В качестве критерия окончания итерационного процесса используется условие малости суммы квадратов внедиагональных элементов:



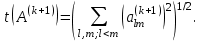
Если 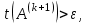то итерационный процесс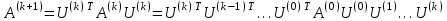

---

продолжается. Если 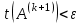, то итерационный процесс останавливается, и в качестве искомых собственных значений принимаются .

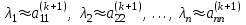Координатными столбцами собственных векторов матрицы в единичном базисе будут столбцы матрицы 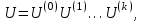т.е.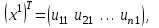



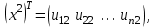
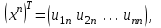
причем эти собственные векторы будут ортогональны между собой, т.е.

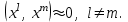
Пример решение проблемы собственных значений в среде MatLab:

Поиск ненулевых решений системы АХ=λX в среде MatLab реализуется командами d=eig(A) или [X,d]=eig(A), где d - диагональная матрица собственных чисел, Х –матрица из нормированных собственных векторов. Например, задав матрицу

	1	2	3
A=	1	4	9
	1	8	27

командой [R,D]=eig(А) получаем:

R =

0.8484 0.7163 -0.1198 -0.5150 0.6563 -0.3295 0.1222 -0.2371 -0.9365

D=

0.2179 0 0 0 1.8393 0 0 0 29.9428

Возьмем другую матрицу

	13	16	16
A=	-5	-7	-6
	-6	-8	-7

---

с известными собственными значениями –3, 1, 1. Выполнив ту же команду [R,D]=eig(А), получаем:

R =

0.8265 0.0000 - 0.8729i 0.0000 +0.8729i -0.4082 -0.0000 + 0.2182i -0.0000 - 0.2182i -0.4082 -0.0000 + 0.4364i -0.0000 - 0.4364i

D=	-3.0 0 0 0 1.0000 + 0.00000003087268i 0 0 0 1.0000 - 0.00000003087268i

Обратите внимание на эффект погрешности (мнимая часть у ряда компонент собственных векторов весьма велика). Поэтому при значительных размерностях и особых случаях (кратные и близкие собственные значения) проверка качества поиска весьма желательна (достаточно проверить на близость к нулю значений A*R-R*D).
Содержание отчета:

1. 
   Титульный лист.
   
2. 
   Цель лабораторной работы.
   
3. 
   Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.
   
4. 
   Расчетная часть: описание выполнения задания
   
5. 
   Проверка результатов в среде MatLab.
   
6. 
   Выводы и анализ полученных результатов.
   

Контрольные вопросы:

1. 
   Что такое собственное число матрицы и как оно вычисляется?
   
2. 
   Что такое собственный вектор и как он находится?
   
3. 
   В чем суть степенного метода;
   
4. 
   Алгоритм вычисления собственного значения и собственного вектора матрицы методом скалярных произведений;
   
5. 
   Метод вращений Якоби численного решения задач на собственные значения и собственные векторы матриц
   
6. 
   Какими командами реализуется поиск ненулевых решений системы АХ=λX в среде MatLab;
   

---

Лабораторная работа №10.

«Интерполирование. Интерполяционные формулы»

Цель: научиться применять интерполяционные формулы для заданной совокупности данных.

Задание:

1. 
   Подобрать интерполяционный полином по формуле Лагранжа для следующей совокупности данных x_i, y_i., найти значение полинома в точке x, найти погрешность. Выполнить эту задачу также в системе MatLab.
   
2. 
   Найти значение полинома в точке x, используя вычислительную схему Эйткина
   

Варианты заданий:

№ Варианта	xi	1	2	3	4	5	x
	yi	0,7	1,9	1,1	2,2	3,5	2.2
	yi	0,8	2,4	1,5	2,3	4,0	5.4
	yi	2,1	3,0	1,5	3,2	4,1	2.3
	yi	2,2	4,8	1,9	3,9	5,5	1.9
	yi	1,0	3,5	5,0	5,6	3,8	3.8
	yi	2,6	1,1	1,6	3,2	2,4	4.1
	yi	3,5	4,8	3,5	1,8	1,5	2.3
	yi	6,0	3,2	1,9	1,3	1,2	1.2
	yi	1,5	1,8	2,5	4,0	7,0	1.1
	yi	0	6,0	2,0	1,3	6,0	3.5
	yi	3,5	1,2	0	1,7	2,0	6.2
	yi	1,4	2,7	6,0	0	4,8	4.6
	yi	2,1	3,1	5,1	5,8	6,0	4,1
	yi	1,3	2,4	6,0	0	4,6	4.2
	yi	3,5	4,8	3,5	1,8	1,5	2.3

---