Файл: Методические указания по выполнению практических работ теория вероятностей и математическая статистика Специальность.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 1007
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
В каких случаях для независимых испытаний удобно составлять биноминальное распределение, а в каких – распределение Пуассона? -
В каких случаях можно составить геометрическое распределение?
ЛИТЕРАТУРА
-
Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2007.
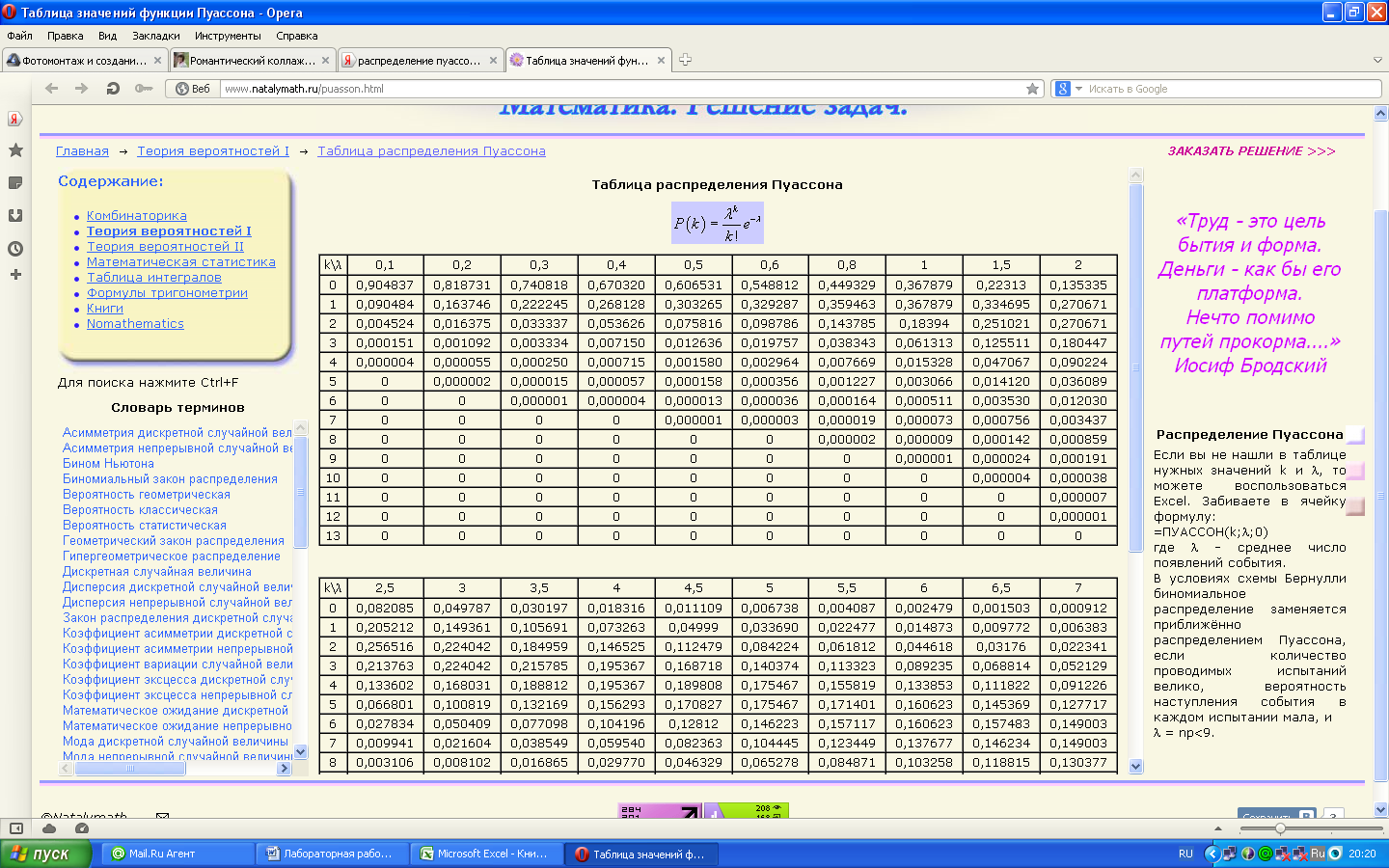
Таблица распределения Пуассона
Практическая работа №8
ВЫЧИСЛЕНИЕ ХАРАКТЕРИСТИК ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
ЦЕЛЬ РАБОТЫ: научиться определять математическое ожидание, дисперсию и среднее квадратичное отклонение дискретной случайной величины по заданному распределению;
Для выполнения работы необходимо знать основы теории вероятностей; необходимо уметь вычислять характеристики дискретных случайных величин.
Выполнение данной практической работы способствует формированию профессиональных компетенций ПК 1.2.Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности; ПК 1.4. Участвовать в экспериментальном тестировании информационной системы на этапе опытной эксплуатации, фиксировать выявленные ошибки кодирования в разрабатываемых модулях информационной системы.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
-
Математическое ожидание случайной величины X определяется по формуле:
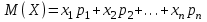
Пример 1. Найти математическое ожидание случайной величины Х, зная ее закон распределения.
| Х | 3 | 5 | 2 |
| р | 0,1 | 0,6 | 0,3 |
Решение
М(Х) = 3*0,1 + 5*0,6 + 2*0,3 = 3,9
Пример 2. Независимые случайные величины Х и Y заданы следующими законами распределения:
| Х | 5 | 2 | 4 |
| Р | 0,6 | 0,1 | 0,3 |
| Y | 7 | 9 |
| Р | 0.8 | 0.2 |
Найти математическое ожидание случайной величины ХY.
Решение.
М(Х) = 5*0,6 + 2*0,1 + 4*0,3 = 4,4
M(Y) = 7*0,8 + 9*0,2 = 7,4
M(XY) = 4,4*7,4=32,56
Пример 3. Производится 3 выстрела с вероятностями попадания в цель, равными р1= 0,4; р2= 0,3; р3 = 0,6. Найти математического ожидание общего числа попаданий.
Решение. Число попаданий при первом выстреле есть случайная величина Х1, которая может принимать только два значения: 1 – попадание с вероятностью 0,4 и 0 – промах с вероятностью 0,6.
М(Х1) = 0,4
Аналогично М(Х2) = 0,3; М(Х3) = 0,6.
Общее число попаданий есть случайная величина, состоящая из суммы попаданий в каждом из выстрелов: Х=Х1+Х2+Х3.
М(Х) = М(Х1+Х2+Х3) = М(Х1) + М(Х2) + М(Х3) = 1,3 попаданий.
Пример 4. Вероятность попадания в цель при стрельбе из орудия р=0,6. Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов.
Решение. Попадание при каждом выстреле не зависит от исходов других выстрелов, поэтому рассматриваемые события независимы и, следовательно, искомое математическое ожидание М(Х) = np = 10*0.6 = 6 попаданий.
- 1 2 3 4 5 6 7 8 9 10
Дисперсия случайной величины определяется по формуле:
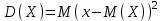 или
или 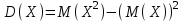
Пример 5. Найти дисперсию случайной величины X, которая задана следующим законом распределения:
| X | 2 | 3 | 5 |
| p | 0,1 | 0,6 | 0,3 |
Решение. Найдем математическое ожидание M(X): M (X)=2*0,1+3*0,6+5*0,3+3,5
Математическое ожидание M(X2)=4*0,1+9*0,6+25*0,3=13,3
Искомая дисперсия: D(X)=M(X2)-[M(X)]2=13,3-(3,5)2=1,05
-
Среднее квадратичное отклонение случайной величины определяется по формуле: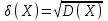
ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ
Задание №1. Найдите математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение
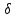 (X).
(X).Вариант 1.
| Х | -1 | -2 | -3 | -10 | -12 | -20 | -30 | -40 |
| Р | 0,1 | 0,1 | 0,1 | 0,09 | 0,3 | 0,009 | 0,3 | 0,001 |
Вариант 2.
| Х | -1 | -2 | -3 | -10 | -12 | -20 | -30 | -40 |
| Р | 0,2 | 0,3 | 0,2 | 0,06 | 0,1 | 0,006 | 0,1 | 0,034 |
Вариант 3.
| Х | -1 | -2 | -3 | -10 | -12 | -20 | -30 | -40 |
| Р | 0,1 | 0,3 | 0,1 | 0,005 | 0,1 | 0,005 | 0,3 | 0,09 |
Вариант 4.
| Х | -1 | -2 | -3 | -10 | -12 | -20 | -30 | -40 |
| Р | 0,2 | 0,4 | 0,1 | 0,002 | 0,1 | 0,09 | 0,1 | 0,008 |
Вариант 5.
| Х | -1 | -2 | -3 | -10 | -12 | -20 | -30 | -40 |
| Р | 0,1 | 0,2 | 0,1 | 0,008 | 0,2 | 0,09 | 0,3 | 0,002 |
Вариант 6.
| Х | -1 | -2 | -3 | -10 | -12 | -20 | -30 | -40 |
| Р | 0,3 | 0,2 | 0,1 | 0,003 | 0,2 | 0,095 | 0,1 | 0,002 |
Задание №2. Дискретные независимые случайные величины заданы законами распределения. Найти математическое ожидание произведения M (XY) и M (2Y).
Вариант 1.:
| Х | 1 | 2 | | Y | 0,5 | 1 |
| р | 0,2 | 0,8 | | р | 0,3 | 0,7 |
Вариант 2.
| Х | 2 | 1 | | Y | 1 | 1,25 |
| р | 0,6 | 0,4 | | р | 0,8 | 0,2 |
Вариант 3.
| Х | 3 | 2 | | Y | 0,65 | 2 |
| р | 0,7 | 0,3 | | р | 0,5 | 0,5 |
Вариант 4.
| Х | 1 | 3 | | Y | 1 | 1,35 |
| р | 0,1 | 0,9 | | р | 0,4 | 0,6 |
Вариант 5.
| Х | 2 | 4 | | Y | 2 | 1,85 |
| р | 0,4 | 0,6 | | р | 0,8 | 0,2 |
Вариант 6.
| Х | 1 | 4 | | Y | 0,4 | 1 |
| р | 0,5 | 0,5 | | р | 0,9 | 0,1 |
Задание №3.
Вариант 1. Производится 4 выстрела с вероятностью по падения в цель р1=0,6 р2=0,4, р3=0,5 и р4=0,7. Найти математическое ожидание общего числа попадания.
Вариант 2. Производится 4 выстрела с вероятностью по падения в цель р1=0,3 р2=0,4, р3=0,6 и р4=0,5. Найти математическое ожидание общего числа попадания.
Вариант 3. Производится 4 выстрела с вероятностью по падения в цель р1=0,1 р2=0,2, р3=0,6 и р4=0,9. Найти математическое ожидание общего числа попадания.
Вариант 4. Производится 4 выстрела с вероятностью по падения в цель р1=0,7 р2=0,2, р3=0,8 и р4=0,5. Найти математическое ожидание общего числа попадания.
Вариант 5. Производится 4 выстрела с вероятностью по падения в цель р1=0,5 р