КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

Среди непрерывных случайных величин особого внимания заслуживают величины, имеющие один из следующих законов распределения: равномерный, показательный, нормальный.

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью:



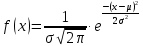
где μ – математическое ожидание; σ – среднеквадратичное отклонение.

Вероятность попадания в интервал нормально распределенной случайной величины равна:

Р(α < X < β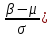) = Ф( - Ф (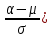 , где Ф – функция Лапласа (определяется по таблице)
Пример 1. Время загрузки Web-страницы распределено нормально, причем его математическое ожидание равно μ = 7 с, а стандартное отклонение σ = 2 с. Определите вероятность того, что время загрузки лежит в интервале 7 – 9 секунд.

Решение

По условию,  = 7,  = 9, μ = 7,  = 2. Следовательно,

P(7 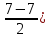– Ф( = Ф(1) – Ф(0) = 0,3413 – 0 = 0,3413.
Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность вероятности постоянна.

Плотность равномерного распределения f(x) определяется формулой:



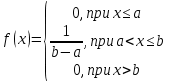
Вероятность попадания в интервал равномерно распределенной
случайной величины


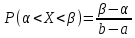
Пример 2. Известно, что передатчик может начать работу в любой момент времени между 12 и 14 часами. Какова вероятность того, что начало передачи придется ждать не более 15 минут (0,25 часа).

Решение. Пусть Х(ч) – время начала работы передатчика. Поскольку передача может начаться в любой момент между 12 и 14 часами и все моменты равновозможны, то Х – случайная величина распределенная равномерно.

 = 12,  = 12,25, а = 12, b = 14

Р(12

---

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью:

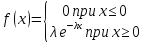, где λ – постоянная положительная величина

Функция показательного распределения определяется формулой:


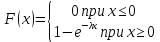
Пример 3. Написать плотность, функцию распределения, математическое ожидание и дисперсию показательного закона, если параметр λ = 8.

Решение

Искомая плотность распределения равна:



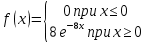
Функция распределения:



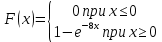
Математическое ожидание М(х) = 1/λ = 1/8

Дисперсия D = 1/λ² = 1/64
ПОРЯДОК ВЫПОЛНЕНИЯ И ФОРМА ОТЧЕТНОСТИ
Задание 1. Решите предложенные задачи

I вариант (на «3»)

1. 
   Передатчик может начать работу в любой момент времени между 10 и 12 часами. Какова вероятность того, что начало передачи придется ждать не более 30 минут. Найти математическое ожидание и стандартное отклонение.
   
2. 
   Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины соответственно равны 8 и 2. Построить график нормально распределенной случайной величины. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (4,8).
   
3. 
   Написать плотность, функцию распределения, математическое ожидание и дисперсию показательного закона, если параметр λ = 5.
   

II вариант (на «3»)

1. 
   Передатчик может начать работу в любой момент времени между 14 и 16 часами. Какова вероятность того, что начало передачи придется ждать не более 45 минут.
   
2. 
   Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины соответственно равны 4 и 2. Построить график нормально распределенной случайной величины. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (4,6).
   
3. 
   Написать плотность, функцию распределения, математическое ожидание и дисперсию показательного закона, если параметр λ = 7.
   

---

III вариант (на «4»)

1. 
   Автобусы маршрута №5 идут строго по расписанию. Интервал движения – 5 минут. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать автобус менее 3 минут. Найти математическое ожидание и стандартное отклонение.
   
2. 
   Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины соответственно равны 10 и 2. Построить график нормально распределенной случайной величины. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (12,14).
   
3. 
   Длительность времени безотказной работы элемента имеет показательное распределение с параметром λ = 0,02. Написать плотность, функцию распределения, математическое ожидание и дисперсию показательного закона. Найти вероятность того, что за время длительностью t = 100 ч элемент откажет.
   

IV вариант (на «4»)

1. 
   Автобусы маршрута №5 идут строго по расписанию. Интервал движения – 5 минут. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать автобус более 3 минут. Найти математическое ожидание и стандартное отклонение.
   
2. 
   Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины соответственно равны 20 и 5. Построить график нормально распределенной случайной величины. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (15,25).
   
3. 
   Длительность времени безотказной работы элемента имеет показательное распределение с параметром λ = 0,005. Написать плотность, функцию распределения, математическое ожидание и дисперсию показательного закона. Найти вероятность того, что за время длительностью t = 200 ч элемент откажет.
   

V вариант (на «5»)

1. 
   Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляются до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана абсолютная ошибка: а) меньшая 0,04; б) большая 0,05.
   
2. 
   Процент содержания золы в угле является нормально распределенной случайной величиной с математическим ожиданием 16% и средним квадратическим отклонением 4%. Определить вероятность того, что в наудачу взятой пробе угля будет от 12 до 24% золы.
   
3. 
   Пусть Х (часть) – время, необходимое для выполнения теста по математике, удовлетворяет показательному распределению с параметром λ=0,25. Написать плотность, функцию распределения, математическое ожидание и дисперсию показательного закона. Вычислить вероятность того, что время, необходимое для выполнения теста, не превысит 4 часов.
   

---

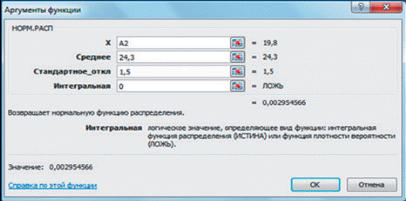
Задание 2. Постройте в электронной таблице кривую Гаусса

1. 
   Столбец А заполняется при помощи автозаполнения значениями от 19,8 до 28,8 с шагом 0,5.
   
2. 
   Для заполнения столбца B используется стандартная функция группы Статистические: НОРМ. РАСП
   
3. 
   Для построения графика функции используется Мастер диаграмм (тип диаграммы – График с маркером).
   
4. 
   Меняя значения математического ожидания и дисперсии распределения, получите различные кривые — «колокола»: крутые или пологие
   

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. 
   Приведите примеры действия нормального и показательного закона распределений в жизни.
   

ЛИТЕРАТУРА

1. 
   Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2007. – 480 с.
   

Практическая работа №12

ПОСТРОЕНИЕ ДЛЯ ЗАДАННОЙ ВЫБОРКИ СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ И ЕГО ГРАФИКА

ЦЕЛЬ РАБОТЫ: научиться строить статические распределения и графически их изображать; научиться определять числовые характеристики выборок.
Для выполнения работы необходимо знать: виды случайных величин, их характеристики и распределения; необходимо уметь: определять вид распределения непрерывной случайной величины, вычислять вероятность попадания непрерывной случайной величины в определенный интервал.

Выполнение данной практической работы способствует формированию профессиональной компетенций ПК 1.2. Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности, ПК 1.4. Принимать участие в приемо-сдаточных испытаниях, ПК 2.3. Применять методики тестирования разрабатываемых приложений.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут.
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Ранжирование предполагает упорядочение данных выборки. В результате ранжирования по возрастанию получается

---

вариационный ряд. Проранжированные данные удобнее записать в виде таблицы, в которой указывается перечень вариант и их частот (относительных частот). Такая таблица называется таблицей частот (относительных частот) или статистическим распределением. Статистические распределения можно также записывать в виде последовательности интервалов и соответствующих им частот.

Для наглядности строятся графики статистического распределения: полигон и гистограмму.

Полигоном частот (относительных частот) называется ломаная, отрезки которой соединяют точки с абсциссами равными вариантам и ординатами, равными частотам (относительным частотам) соответствующих вариантов.

Гистограммой частот (относительных частот) называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых случат частичные интервалы длиной h, а высоты равны отношению n/h (W/h).
Пример 1. Дан статистический ряд: 2 2 3 3 3 3 4 2 3 3 2 3 2 3 2 3 2 4 3 2 2 3 2 4 5 2 3 3 2 4 3 2 3 4 3 3 2 3 5 3.

а) построить для него вариационный ряд; б) построить статистическое распределение для частот и относительных частот; в) дополнить статистическое распределение накопленными частотами;

г) построить полигон частот и относительных частот.

Решение

а) Для получения вариационного ряда сгруппируем одинаковые значения исходного ряда и запишем их в порядке возрастания: 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 5.

б) Подсчитав частоты каждой варианты, построим статистическое распределение. Для нахождения относительных частот используем формулу: W_i = n_i/n (где n – объем выборки). В нашем примере n = 40.

xi	2	3	4	5
ni	14	19	5	2
Wi	0,35	0,475	0,125	0,05

в) Накопленная частота S_i показывает, какая доля чисел статистического ряда не превышает данного значения. Накопленные частоты получаются из относительных частот накопительным суммированием.

---

Смотрите также файлы

• перпендикулярные прямые.docx

• Разработка урока в рамках формирования универсальных учебных действий (на примере темы Буквы Ш,ш, обозначающие согласный звук (ш, ) по учебному предмету русский язык (обучение грамоте).docx

• Добрый вечер, Алексей!.pdf

• Занятие для обучающихся 89 классов по теме день конституции.pdf

• Теоретические основы доступа информации как проблема региональной журналистики 5.doc