Файл: Учебное пособие по дисциплине Механика Модуль Прикладная механика.docx

 

Силы инерции звеньев и моменты сил инерции. 
Так как звенья механизма находятся в движении, и имеют свои массы, то, особенно в быстродействующих  механизмах рычажного типа, обязательно имеет место неравномерность движения звеньев. Это означает, что ускорения этих звеньев не равны нулю, что приводит к возникновению дополнительных сил динамического характера в виде сил инерции   и моментов инерции  . Из теоретической механики известно, что все силы инерции звена, совершающего плоскопараллельное движение и имеющего плоскость симметрии, параллельную плоскости движения, могут быть сведены к силе инерции  , приложенной в центре масс S звена, и паре сил инерции, момент которых обозначим   (рис. 9.30).



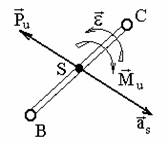
Рис. 9.30. Сила инерции звена и момента сил инерции

 

– главный вектор сил инерции, или сила инерции;

 – главный момент сил инерции, или момент сил инерции;m – масса звена;

 – массовый  момент  инерции  относительно центра  масс;

 – ускорение  центра  масс;

– угловое ускорение звена.

 и   направлены в стороны, противоположные ускорениям  и  .
Статическая определимость кинематической цепи

При силовом анализе механизмов (определении неизвестных сил, действующих на движущиеся звенья) можно использовать уравнения (законы) статики. Докажем это положение, проанализировав реакции в кинематических парах (табл. 9.2).

 Таблица 9.2.

Кинематические пары	Равновесие каждого звена	Известные параметры	Неизвестные параметры
5-й класс Вращательная		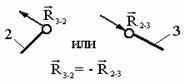Точка приложения	Величина, направление
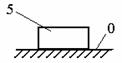Поступательная		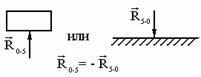Направление	Величина, точка приложения
4-й класс		Точка приложения, направление	Величина

---

Примечание. 2, 3, 5 – номера звеньев.

 

В кинематических парах 5-го класса известно по одному параметру сил реакций, неизвестны два, в кинематических парах 4-го класса известны два параметра, а неизвестен один.

Таким образом, плоская кинематическая цепь, состоящая из кинематических пар 5-го и 4-го классов, имеет 2Р₅ + Р₄ неизвестных величин сил реакций.

В то же время для одного звена можно составить 3 уравнения статики, а для n звеньев – 3n уравнений статики.

Кинематическая цепь будет статически определима, если число неизвестных величин сил реакций не превышает числа возможных уравнений статики, т.е.

3n = 2P₅ + Р₄.

Это и есть условие статической определимости кинематической цепи.

Полученное равенство можно записать в виде

3n – 2Р₅ – Р₄ = 0.

Но запись слева от знака равенства является числом степеней свободы кинематической цепи W, т.е.

W = 3n – 2Р₅ – P₄ = 0.

Таким свойством (W=0) обладают структурные группы, или группы Ассура –статически определимые кинематические цепи.

 Силовой анализ механизма с учетом сил трения

9.6. Трение в механизмах. Виды трения.
Способность контактирующих поверхностей звеньев сопротивляться их относительному движению называется внешним трением. Трение обусловлено неидеальным состоянием контактирующих поверхностей (микронеровности, загрязнения, окисные пленки и т.п.) и силами межмолекулярного сцепления. Трение в кинематических парах характеризуется силами трения и моментами сил трения. Силой трения называется касательная составляющая реакции в кинематической паре (составляющая направленная по касательной к контактирующим поверхностям), которая всегда направлена против вектора скорости относительного движения звеньев.

Различают следующие виды трения:

- трение покоя проявляется в момент, когда два тела находящиеся в состоянии относительного покоя начинают относительное движение (касательную составляющую  возникающую в зоне контакта до возникновения относительного движения, в условиях когда она меньше силы трения покоя, будем называть силой сцепления; максимальная величина силы сцепления равна силе трения покоя);

- трение скольжения появляется в кинематической паре при наличии относительного движения звеньев; для большинства материалов трение скольжения меньше трения покоя;

---

- трение качения появляется в высших кинематической паре при наличии относительного вращательного движения звеньев вокруг оси или точки контакта;

- трение верчения возникает при взаимодействии торцевых поверхностей звеньев вращательных кинематической паре (подпятники).

Сила трения покоя зависит от состояния контактных поверхностей звеньев, а сила трения скольжения - также и от скорости скольжения.
 Теоретические основы определения коэффициента трения

Трение в поступательной кинематической паре

При перемещении одного тела (звена механизма) относительно находящегося с ним в контакте другого тела (звена) в месте их контакта возникает сила, сопротивляющаяся перемещению, – сила трения F (рис. 9.31).

Величину коэффициента трения в поступательной кинематической паре можно определить с помощью так называемого закона Кулона, в соответствии с которым величина силы трения F прямо пропорциональна нормальной силе N между соприкасающимися звеньями. Векторная сумма сил и   равна полной силе реакций в кинематической паре:   (рис. 30).



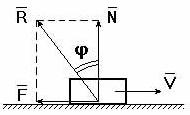
Рис. 9.31. Схема сил в поступательной кинематической паре

 

Отношение   называют коэффициентом трения скольжения в поступательной кинематической паре, а угол   – углом трения скольжения.

Полная реакция  отклоняется на угол трения   в сторону, противоположную скорости   (см. рис. 4.16).

Величину коэффициента трения скольжения f можно определить экспериментально или по справочникам (величина f зависит от шероховатости, материалов, трущихся поверхностей, наличия смазки, ее качества, температуры и т.д.).

 

Трение во вращательной кинематической паре
Внешние нагрузки, действующие на вал при его вращении, показаны на схеме рис. 9.32.



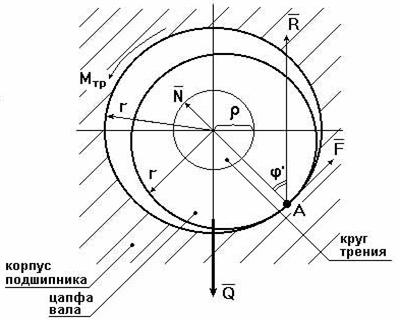
Рис. 9.32. Схема сил во вращательной кинематической паре
Здесь А – точка приложения нормальной реакции  , причем   – равнодействующая всех нормальных сил (эпюра этих сил может иметь различный вид), (рис. 32);  – сила трения (равно-действующая всех сил трения, распределенных по поверхности контакта); – сила давления цапфы вала на опору (корпус подшипника);   – сила реакции во вращательной  кинематической паре,  ;  ;   – угол трения; 

---

r – радиус цапфы (опорной части) вала;   – радиус круга трения;   – приведенный коэффициент трения.

Во вращательной кинематической паре реакция   отстоит от оси вращения на величину радиуса круга трения  , причем   всегда касательна к кругу трения.

Момент трения  .

Величину   можно определить:

– экспериментально (например, используя метод выбега);

– по эмпирическим формулам с учетом износа подшипника и соответствующего изменения эпюр давления (рис. 32): для нового подшипника  , для изношенного –  , где f – коэффициент трения скольжения в поступательной кинематической паре (берется из справочников).

            



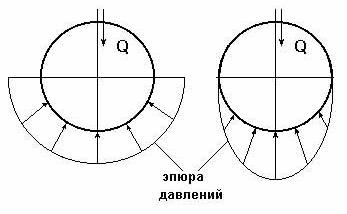
                           а)                                                          б)

Рис. 9.33. Примерные схемы эпюр давления в новом

(а) и изношенном (б) подшипниках скольжения

 

Трение качения в высшей кинематической паре
Картину внешних сил и эпюр распределения давлений в месте контакта тел качения можно условно отобразить на нижеприведенных схемах (рис. 9.34). В состоянии покоя эпюра напряжений в зоне контакта симметрична относительно общей нормали, проведенной через условную точку касания, а равнодействующая силаN совпадает с нормалью. При качении симметрия эпюры нарушается, а силаN смещается в направлении качения на расстояние k.

 



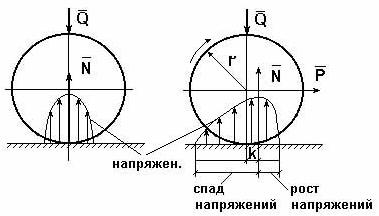
                    а)                                                         б)
Рис. 9.34. Примерные схемы сил и эпюр давления в зоне контакта цилиндра

с плоскостью: а) состояние покоя; б) состояние перекатывания

 

Здесь   – равнодействующая сила давлений в месте смятия соприкасающихся звеньев (тел качения);   – нагружающая сила, ;   – момент трения качения;   – плечо силы трения качения или коэффициент трения качения (имеет размерность длины);   – сила перекатывания.

Условие равновесия перекатывающегося тела в форме моментов можно записать как  , откуда  .

 
9.7. Динамика машин и механизмов.

 

Общие положения

Динамика - раздел механики машин и механизмов, изучающий закономерности движения звеньев механизма под действием приложенных к ним сил. Имеется такое определение: “Динамика рассматривает силы в качестве причины движения тел”. В основе динамики лежат три закона, сформулированные Ньютоном, из которых следует:

---

Из первого закона: Если равнодействующая всех внешних сил, действующих на механическую систему равно нулю, то система находится в состоянии покоя.

Из второго закона: Изменение состояния движения механической системы может быть вызвано либо изменением действующих на нее внешних сил, либо изменением ее массы.

Из этих же законов следует, что динамическими параметрами механической системы являются:

- инерциальные (массы mи моменты инерции I);

- силовые (силы F_ij и моменты сил M_ij);

- кинематические (линейные aи угловые   ускорения).

Динамическая модель - модель системы, предназначенная для исследования ее свойств в функции времени (или модель системы, предназначенная для исследования в ней динамических явлений).

Прямая задача динамики - определение закона движения системы при заданном управляющем силовом воздействии.

Обратная задача динамики- определение требуемого управляющего силового воздействия, обеспечивающего заданный закон движения системы.

Методы составления уравнений (динамической модели системы):

- энергетический (уравнения энергетического равновесия - закон сохранения энергия);

- кинетостатический (уравнения силового равновесия с учетом сил инерции по принципу Д’Аламбера).

Задачами динамического анализа и синтеза механизма, машины являются изучение режимов движения с учетом действия внешних сил и установление способов, обеспечивающих заданные режимы движения. При этом могут определяться мощности, необходимые для обеспечения заданного режима движения машины, проводиться сравнительная оценка механизмов с учетом их механического коэффициента полезного действия, устанавливаться законы движения ведущего звена (например, колебания угловой скорости кривошипа за один оборот) под действием внешних сил, приложенных к звеньям механизма, а также решаться задачи подбора оптимальных соотношений между силами, массами, размерами звеньев механизмов.

В динамике машин объектом изучения (исследования) является машинный агрегат. В общем виде его можно представить как механическую систему, состоящую из трех основных частей: машина-двигатель, передаточный механизм и рабочая машина (или исполнительный механизм).

В машине-двигателе какой-либо вид энергии преобразуется в механическую энергию, необходимую для приведения в движение рабочей машины. Например, в электродвигателе электрическая энергия преобразуется в механическую, а в двигателе внутреннего сгорания в механическую энергию преобразуется тепловая энергия сгорания топлива.

---