Файл: Учебное пособие по дисциплине Механика Модуль Прикладная механика.docx

Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.

Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.

Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 3.1.

 



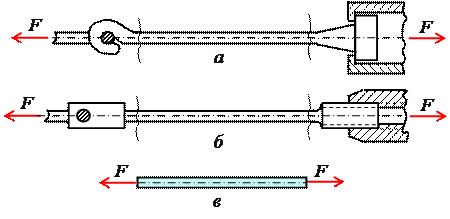
Рис. 3.1

 

Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 3.1, а, б) оказывается единой (рис. 3.1, в) согласно принципу Сен – Венана.

Если воспользоваться методом сечений (рис. 3.2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы N_z, равные силе F (рис. 3.2, б).

Сжатие отличается от растяжения, формально говоря, только знаком силы N_z. При растяжении нормальная сила N_z  направлена от сечения (рис. 3.2, б), а при сжатии – к сечению.


Рис. 3.2

 

Растягивающие продольные силы принято считать положительными (рис. 3.3, а), а сжимающие – отрицательными(рис. 3.3, б).
 



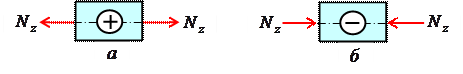
Рис. 3.3

 

При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от N_z), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.

Продольные силы (N_z), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.

График, показывающий изменение продольных сил по длине оси стержня, называется 

---

эпюрой продольных сил (эп.N_z). Он дает наглядное представление о законе изменения продольной силы.

 Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.

Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти N_max при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.

Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.

Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.

Рассмотрим стержень постоянного поперечного сечения, жестко защемленный правым концевым сечением и нагруженный заданной внешней сосредоточенной нагрузкой F и распределенной q (рис. 3.4, а).

Прежде всего определим опорную реакцию R₁, задавшись ее направлением вдоль оси z.

ΣF_z=0,   -R₁ - 22 + 24∙0,6 = 0,    R₁= -7,6 кН.

Знак минус говорит о том, что действительное направление опорной реакции R₁ противоположно показанному на рис. 3.4, а. Исправляем его и в дальнейших расчетах знак минус у опорной реакции R₁ не учитываем (рис. 3.4, в, г).

Под участкомбудем понимать часть стержня, на которой N_z  представляется некоторым аналитическим выражением. На другом участке N_z  будет определяться другой функцией.

Границами участка являются начало и конец стержня, сечения, где приложены сосредоточенные нагрузки, начинается и заканчивается распределенная нагрузка.

В нашем случае стержень разбивается на два участка. В пределах первого участка мысленно рассечем стержень на две части нормальным сечением (рис. 3.4, 

---

б, в).



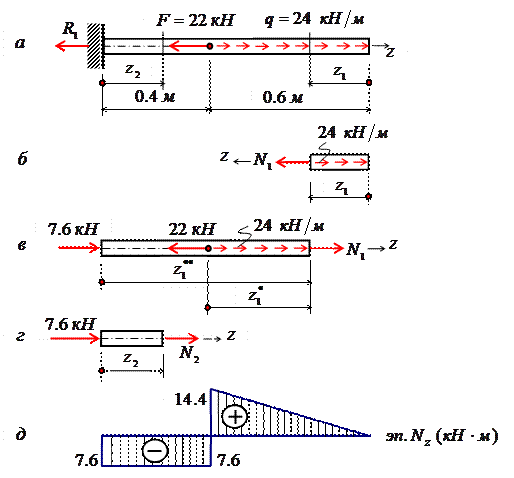
Рис. 3.4

 

Направления продольных сил (рис. 3.4, б – г) приняты в предположении, что они являются растягивающими (т. е. положительными). Если в результате расчета значение N_i получится со знаком «минус», то это будет означать, что в действительности стержень в этом сечении сжат.

Поскольку обе части стержня являются равноправными, то N₁ на первом участке в сечении, определяемом координатой z₁, можно определить рассматривая равновесие его правой (рис. 3.4, б) либо левой (рис. 2.4, в) частей.

В нашем случае для определения N₁ предпочтительнее рассмотреть равновесие правой части – к ней приложено меньше сил (рис. 3.4, б). Начало координат совмещаем с правым концевым сечением первого участка. Ось z направляем налево. Пределы изменения положения сечения вдоль продольной оси  0≤z₁≤0,6 м. Спроектируем все силы, действующие на правую часть, на продольную ось.

ΣF_z=0,   N₁ - 24∙z₁ = 0,    N₁ =24∙z₁,   N₁(0)= 0,    N₁(0,6)= 14,4 кН.

Поскольку функция N₁ =24∙z₁ получилась линейная, то для построении графика ее изменения вдоль продольной оси (эп.N_z) достаточно вычислить значения продольной силы на границах первого участка, отложить их перпендикулярно продольной оси вверх (стержень растянут) и провести через них прямую линию (рис. 3.4, д).

Таким образом, в пределах первого участка стержень растянут и нормальная сила изменяется по линейному закону.

Этот же результат можно получить, рассматривая равновесие левой части стержня.

Здесь при выборе системы координат рассмотрим два варианта. При первом варианте начало координат совмещаем с левым концевым сечением второго участка. Ось z направляем направо. Пределы изменения положения сечения вдоль продольной оси 0,4 м≤ ≤1,0 м. Спроектируем все силы, действующие на левую часть, на продольную ось.

ΣF_z=0,   N₁ +7,6 – 22 + 24∙(  - 0,4)= 0,    N₁ =24- 24∙ ,   N₁(0,4)= 14,4 кН,    N₁(1,0)= 0.

Во втором варианте введем скользящую систему координатных осей. Начало координат совмещаем с левым концевым сечением первого участка. Ось z направляем направо. Пределы изменения положения сечения вдоль продольной оси 0≤ ≤0,6 м. Имеем

ΣF_z=0,   N₁ +7,6 – 22 + 24∙  = 0,    N₁ =14,4- 24∙ ,   

---

N₁(0)= 14,4 кН,    N₁(0,6)= 0.

Заметим, что при выборе скользящей системы координат, функция N₁=f(z, q) меняется от нуля, что делает последующие расчеты менее трудоемкими.

Сравнивая все три варианта определения N₁, приходим к выводу, что когда мы оставляем ту часть стержня, к которой приложено меньше внешних нагрузок, то расчеты оказываются более простыми.

При некотором навыке можно сразу составить выражение для N₁, не изображая отдельные части бруса, на которые он расчленяется поперечными сечениями (рис. 3.4, б, в). Например,

при  0≤z₁≤0,6 м,  N₁ =24∙z₁;  

при  0,4 м≤ ≤1,0 м,  N₁ =7,6 + 22 - 24∙( -0,4);

при 0≤ ≤0,6 м,  N₁ = -7,6 + 22 - 24∙ .

Таким образом, на основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.

Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.

Осталось определить значение продольной силы N₂ в произвольном сечении, определяемом координатой z₂, на втором участке (рис. 3.4, г). Так как продольная сила N₂ численно равна алгебраической сумме внешних сил, приложенных к стержню слева от сечения (рассматриваем равновесие левой части стержня), то N₂= -7,6 кН (реакция R₁=7,6 кН сжимает часть стержня длиной z₂). Здесь принимаем скользящую систему координат, с началом в левом концевом сечении второго участка. Ось z направляем направо.

Эпюра N_z на втором участке представлена на рис 3.4, д в виде прямоугольника со знаком минус, поскольку N₂= -7,6 кН =const. Таким образом, в пределах второго участка стержень претерпевает сжатие постоянной нормальной силой.

Каждая ордината эп.N_z  (рис. 3.4, д) в принятом масштабе равна величине продольной силы, действующего в том поперечном сечении стержня, которому соответствует эта ордината.

Видно, что на участке между точками приложения сосредоточенных сил R₁ и  F  продольная сила имеет постоянное значение, а на участке, где приложена распределенная внешняя нагрузка, меняется по линейному закону (рис. 3.4, д).

Характерно, что скачки на эп.N_z  обусловлены наличием в соответствующих сечениях сосредоточенных сил 

---

R₁ и F.

3.2. Напряжение в поперечных сечениях стержня
Нормальная сила N приложена в центре тяжести сечения, яв­ляется равнодействующей внутренних сил в сечении и, в соответст­вии с этим, определяется следующим образом:



Но из этой формулы нельзя найти закон распределения нор­мальных   напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.

Если на боковую поверхность этого стержня нанести прямо­угольную сетку (рис. 3.2, б), то после нагружения поперечные ли­нии аа, bb и т.д. переместятся параллельно самим себе, откуда следует, что все поверхностные продольные волокна удлинятся одинаково. Если предположить также, что и внутренние волокна работают таким же образом, то можно сделать вывод о том, что по­перечные сечения в центрально растянутом стержне смещаются параллельно начальным положениям, что соответствуетгипотезе плоских сечений (гипотезе Бернулли).

Значит, все продольные волокна стержня находятся в одина­ковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть также одинаковы и рав­ны



где A  площадь поперечного сечения стержня.

В сечениях, близких к месту приложения внешних сил, гипотеза Бернулли нарушается: сечения искривляются, и напряжения в них распределяются неравномерно. По мере удаления от сечений, в которых приложены силы, напряжения выравниваются, и в сечениях, удаленных от места приложения сил на расстояние, равное наибольшему из размеров поперечного сечения, напряжения можно считать распределенными по сечению равномерно. Это положение, называемое принципом Сен-Венана, позволяет при определении напряжений в сечениях, достаточно удаленных от мест приложения внешних сил, не учитывать способ их приложения, заменять систему внешних сил статически эквивалентной системой. Например, экспериментально установлено, что во всех трех случаях нагружения стержня (рис. 3.7, а) значения напряжений в сечениях, удаленных от крайних сечений на расстояние не менее высоты сечения h, одинаковы:   (рис. 3.7, б), а в сечениях, близких к местам приложения внешних сил, распределения напряжений по сечению существенно различны (рис. 3.7, 

---