Файл: Учебное пособие по дисциплине Механика Модуль Прикладная механика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 706
Скачиваний: 1
СОДЕРЖАНИЕ
7.2.Изгиб с растяжением (сжатием)………………….……………………………….92
7.3.Внецентренное сжатие или растяжение………………….………………………93
Вопросы для самопроверки……………………………………………………………99
8.Прочность при переменных и циклически изменяющихся напряжениях…………………………………………………………………………….100
8.1.Усталость и выносливость материалов…………………….……………………100
8.2.Основные характеристики цикла и предел усталости……………….…………102
8.3.Расчет коэффициентов запаса усталостной прочности………………….……...104
Библиографический список………………………………………………..………152
АННОТАЦИЯ ДИСЦИПЛИНЫМЕХАНИКА. МОДУЛЬ ПРИКЛАДНАЯ МЕХАНИКА
1.9. Общие принципы расчета конструкции
3. Осевое растяжение – сжатие.
4. Геометрические характеристики плоских сечений
5.1. Основные понятия. Крутящий момент
Условие прочности при кручении вала круглого и кольцевого сечения
7.1.Расчет балки, подверженной косому или пространственному изгибу
7.2. Изгиб с растяжением (сжатием)
8. Прочность при переменных и циклически изменяющихся напряжениях
5. Кручение, сдвиг, срез
5.1. Основные понятия. Крутящий момент
Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент Mk, (другое обозначение T, Mz), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.
Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси..
Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.
Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.
Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.
Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.
При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от Mk), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.
При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.
Построение эпюр крутящих моментов
Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов Mk (Mz) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений
, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.
В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣMz=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 5.1, крутящий момент Mz в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M1|=|M2|.
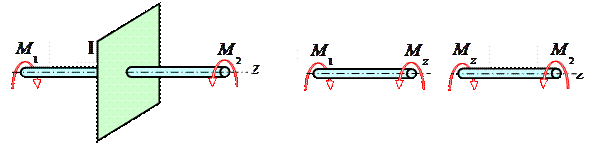
Рис. 5.1
В более сложных случаях, когда к валу приложено несколько внешних моментов, крутящие моменты Mk в поперечных сечениях различных участков вала неодинаковы.
На основании метода сечений крутящий момент в произвольном поперечном сечении вала численно равен алгебраической сумме внешних скручивающих моментов, приложенных к валу по одну сторону от рассматриваемого сечения.
При расчетах на прочность и жесткость знак крутящего момента не имеет никакого значения, но для удобства построения эп. Mk примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части вала действующий на него момент представляется направленным по ходу часовой стрелки (рис.5.2).
В технике употребляется терминология « винт с правой нарезкой» или «…с левой нарезкой…», причем правый винт наиболее распространен, являясь стандартом. Полезно заметить, что при навинчивании гайки на правый винт мы прикладываем положительный момент Mкр , а при свинчивании гайки – отрицательный.

Рис. 5.2
На рис. 5.3, а изображен стержень, жестко защемленный в правом концевом сечении, к которому приложены три внешних скручивающих момента.
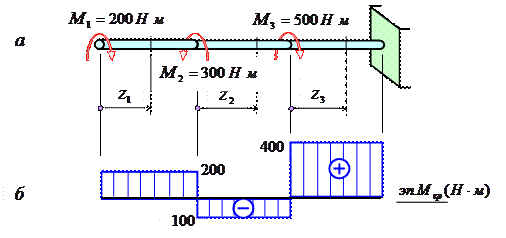
Рис. 5.3
В нашем случае крутящие моменты в их поперечных сечениях удобно выражать через внешние моменты, приложенные со стороны свободного конца бруса.
Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.
Крутящий момент Mz1 в сечении I численно равен
M1=200 нм и, согласно принятому правилу знаков, положителен.
Крутящий момент Mz2 в сечении II численно равен алгебраической сумме моментов M1 и M1, т.е. Mz2 =200-300=-100 нм, а его знак зависит от соотношения этих моментов.
Аналогичным образом вычисляется крутящий момент Mz3 в сечении III: Mz3 =200-300+500=400 нм.
Изменение крутящих моментов по длине вала покажем с помощью эпюры крутящих моментов. На рис. 5.3, б показана такая эпюра для стержня, изображенного на рис. 5.4, а.
Каждая ордината эп. Mk в принятом масштабе равна величине крутящего момента, действующего в том поперечном сечении бруса, которому соответствует эта ордината.
В сечении, в котором к брусу приложен внешний скручивающий момент, ордината эпюры изменяется скачкообразно на величину, равную значению этого момента.
Напряжения в поперечном сечении
Опыты показывают, что если на поверхности бруса круглого сечения нанести прямоугольную сетку, а на торцевой поверхности нанести радиальные линии (рис.5.5), то после деформации кручение окажется что:
- все образующие поворачиваются на один и тот же угол , а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;
- торцевые сечения остаются круглыми, плоскими, расстояния между ними не меняются;
- каждое сечение поворачивается относительно другого на некоторый угол , называемый углом закручивания;
- радиальные линии на торцевой поверхности остаются прямыми.
На основании этих наблюдений можно заключить, что может быть принята гипотеза Бернулли (гипотеза плоских сечений), а в вале возникают условия чистого сдвига, в поперечных сечениях действуют только касательные напряжения, нормальные напряжения равны нулю.
Рассмотрим поперечное сечение вала, расположенное на некотором расстоянии z от торцевого, где Мк=T (рис.5.4). На элементарной площадке dF будет действовать элементарная сила , момент который относительно оси вала равен . Крутящий момент Мк, в сечении равен
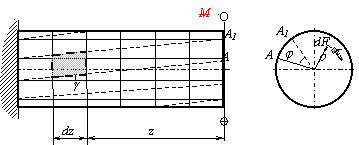
Рис.5.4
Для того чтобы проинтегрировать это выражение необходимо знать закон распределения напряжений в сечении. Выделим из вала элементарное кольцо длиной dz и толщиной (рис.5.5).
Правый торец элемента повернется относительно левого на угол , образующая СВ повернется на угол и займет положение СВ1. Угол - относительный сдвиг. Из треугольника ОВВ1 найдем:
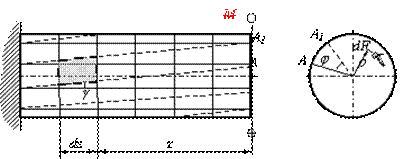
Рис.5.5 Рис.5.6
Из треугольника СВВ1: . Откуда, приравнивая правые части, получим
На основании закона Гука при сдвиге:
Подставим выражение (5.2) в (5.1):
Откуда
Подставим значение в выражение (5.4) получим:
Таким образом, касательные напряжения при кручении прямо пропорциональны расстоянию от центра тяжести сечения до рассматриваемой точки и одинаковы в точках, одинаково удаленных от центра тяжести сечения (рис. 5.6). При получим . Наибольшие напряжения возникают в точках контура сечения при :
Величина отношения полярного момента инерции к радиусу вала называется моментом сопротивления сечения при кручении или полярным моментом сопротивления
Для сплошного круглого сечения
Для кольцевого сечения
где
Тогда максимальные касательные напряжения равны