Файл: Учебное пособие по дисциплине Механика Модуль Прикладная механика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 760
Скачиваний: 1
СОДЕРЖАНИЕ
7.2.Изгиб с растяжением (сжатием)………………….……………………………….92
7.3.Внецентренное сжатие или растяжение………………….………………………93
Вопросы для самопроверки……………………………………………………………99
8.Прочность при переменных и циклически изменяющихся напряжениях…………………………………………………………………………….100
8.1.Усталость и выносливость материалов…………………….……………………100
8.2.Основные характеристики цикла и предел усталости……………….…………102
8.3.Расчет коэффициентов запаса усталостной прочности………………….……...104
Библиографический список………………………………………………..………152
АННОТАЦИЯ ДИСЦИПЛИНЫМЕХАНИКА. МОДУЛЬ ПРИКЛАДНАЯ МЕХАНИКА
1.9. Общие принципы расчета конструкции
3. Осевое растяжение – сжатие.
4. Геометрические характеристики плоских сечений
5.1. Основные понятия. Крутящий момент
Условие прочности при кручении вала круглого и кольцевого сечения
7.1.Расчет балки, подверженной косому или пространственному изгибу
7.2. Изгиб с растяжением (сжатием)
8. Прочность при переменных и циклически изменяющихся напряжениях
Например, необходимо определить скорость точки S2, принадлежащей шатуну 2 и расположенной на середине отрезка АВ. Используя теорему подобия, на отрезке ab плана скоростей находят его середину (точка S2), которая, будучи соединенной с полюсом Рv, даст вектор VS2, изображающий абсолютную (полную) скорость точки S2.
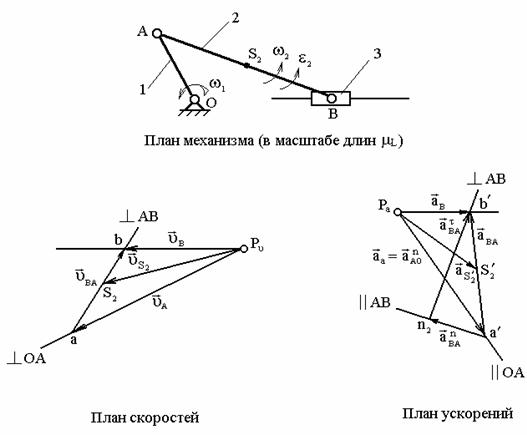
Рис. 9.28. Построение планов скоростей и ускорений
кривошипно-ползунного механизма
Рассчитаем величину линейных скоростей и угловую скорость шатуна:
, м/с,
, м/с,
, м/с,
, с-1.
Направление вектора угловой скорости шатуна определяется следующим образом. Вектор скорости VВА условно переносится в точку В плана механизма. Куда он будет вращать шатун относительно точки А, в ту сторону и направлена угловая скорость шатуна.
План ускорений кривошипно-ползунного механизма строят после того, как будет составлено векторное уравнение ускорений шатуна, учитывая, что он совершает сложное движение:
где аА – ускорение точки А; его величину и направление можно определить, используя векторное уравнение ускорения точки А относительно оси О вращения кривошипа:
причём ускорение точки А относительно О можно разложить на две составляющие – нормальное ускорение и тангенциальное , т.е.
Так как точка О неподвижна и ускорение её равно нулю ( и при условии, что угловая скорость вращения кривошипа постоянна: и его угловое ускорение ), то векторное уравнение ускорения точки А можно записать в виде
Величина нормальной составляющей ускорения (нормальное ускорение) рассчитывается по формуле
(его вектор направлен по радиусу вращения кривошипа от точки А к точке О).
Затем вычисляется нормальное ускорение точки В относительно А по формуле
(его вектор направлен от В к А).
После выбора масштаба плана ускорений по формуле
величина нормального ускорения переводится этим масштабом в векторный отрезок длиной
, мм.
Затем строится план ускорений (см. рис. 9.28). Из произвольно выбранного полюса
Ра параллельно отрезку ОА плана механизма проводится вектор ускорения , длина которого была выбрана произвольно при расчёте масштаба . Из конца этого вектора (точки ) проводится вектор ускорения длиной , который должен быть параллелен отрезку АВ плана механизма и направлен от точки В к А. Перпендикулярно ему через точку n2 проводят прямую до пересечения с прямой, проведённой через полюс Ра параллельно линии движения ползуна 3. Полученная точка их пересечения b' определяет длины векторов ускорений aBA и aB.
Для нахождения величины ускорения точки S2, принадлежащей шатуну, можно применить теорему подобия. При этом необходимо на векторе, изображающем на плане ускорений относительное ускорение aBA, найти соответствующую точку S2', делящую отрезок a'b' в той же пропорции, что и точка S2 делит отрезок АВ на плане механизма.
Угловое ускорение шатуна вычисляется по формуле
, с-1,
где n2b' – длина вектора на плане ускорений, изображающего тангенциальное ускорение .
Для определения направления вектора углового ускорения шатуна необходимо вектор тангенциального ускорения условно перенести в точку В плана механизма. Куда он будет вращать шатун относительно точки А, в ту сторону и направлено ускорение шатуна.
Аналитический метод кинематического анализа
Общие сведения о методе
Графический (метод диаграмм) и графоаналитический методы (метод планов скоростей и ускорений) кинематического анализа механизмов имеют недостатки: невысокая точность, определяемая точностью графических построений, и большая трудоёмкость.
Эти недостатки отсутствуют в аналитическом методе. Но при этом необходимо составлять достаточно сложные аналитические зависимости (формулы) и иметь возможность решать их с использованием компьютерных техники и технологии, что в последнее время возможно и доступно.
Методы аналитического исследования:
метод замкнутых векторных контуров (метод Зиновьева) удобен для кинематического анализа практически всех используемых в технике несложных рычажных механизмов;
метод преобразования координат (метод Морошкина) удобен для кинематического анализа многозвенных механизмов типа манипуляторов промышленных роботов.
Прежде чем говорить об аналитическом методе, введем некоторые понятия и определения.
Функция положения. Аналог скорости. Аналог ускорения
Положение любого звена механизма может определяться параметрами: углом относительно какой-либо координатной оси или координатами ХК и YК (рис. 9.29).
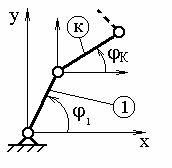
Рис. 9.29. Схема механизма
Функция положения – это аналитическая зависимость положения или координаты К-го звена ( , ХК или YК ) от положения ведущего звена , т.е. или и , где , XK и YK – координаты, определяющие положение К-го звена (ведомого), а угол – угол, характеризующий положение ведущего звена.
Аналог скорости. Угловая скорость К-го звена определяется зависимостью
где – аналог скорости К-го звена (первая передаточная функция) для вращающегося звена, величина безразмерная; и – аналоги скорости К-го звена, движущегося поступательно, величины безразмерные.
Аналог ускорения. Угловая скорость К-го звена определяется зависимостью, получаемой дифференцированием уравнения (3) по dt:
Введение в кинематический анализ понятий аналогов отделяет геометрические свойства механизма от кинематических.
Величину называют ещё передаточным отношением, так как выражение можно преобразовать, умножив и разделив его на величину dt:
Для решения задачи о положениях звеньев исследуемого механизма необходимо найти функции положения ( или ХК и YК ), предварительно составив векторное уравнение замкнутого векторного контура кинематической цепи и уравнения проекций его на координатные оси Х и Y. Из этих уравнений находят функции положения (зависимости положений исследуемого звена от положения ведущего звена). При известном (заданном) законе движения ведущего звена задаются шагом и вычисляют координаты исследуемых звеньев (угловые координаты для вращающегося звена и прямоугольные для звена, совершающего возвратно-поступательное движение).
Для решения задачи о скоростях необходимо найти аналоги скоростей исследуемых звеньев и, умножив их на угловую скорость ведущего звена, получить формулы расчета искомых скоростей.
Для решения задачи об ускоренияхнаходят также аналоги ускорений звеньев и по формулам, приведенным в таблице, находят величины ускорений. Ниже приводится пример кинематического анализа кривошипно-ползунного механизма аналитическим методом.
9.5. Силовой (кинетостатический) анализ механизмов.
Проектирование нового механизма всегда включает его силовое исследование, так как по найденным силам производится последующий расчет на прочность элементов кинематических пар и звеньев механизма.
Силы, действующие в механизмах
Различают две группы внешних сил.
Движущие силы Рдв или моменты движущих сил Мдв, которые:
- совершают положительную работу;
- направлены в сторону скорости точки приложения силы или под острым углом к ней;
- задаются посредством механической характеристики двигателя.
Пример: силы давления газа на поршень в двигателе внутреннего сгорания, силы веса при опускании груза и т.д.
Силы сопротивления РС и их моменты МС, которые:
- совершают отрицательную работу;
- направлены противоположно скорости.
В свою очередь силы сопротивления делятся на силы:
- полезного сопротивления Рп.с и моменты Мп.с (силы тяжести при подъеме груза);
- вредного сопротивления: трение в кинематических парах, сопротивление среды, внутреннее сопротивление (например, силы упругости звеньев).
Кроме этого существуют:
- силы веса (тяжести) , где – масса звена в кг; м/с2 – ускорение свободного падения. При кинематическом исследовании считают, что сила тяжести приложена в центре тяжести звена. Если звено выполнено в виде стержня, то его ц.т. расположен в центре симметрии звена, а если в виде ползуна, то в центре шарнира. Силы тяжести в течении расчётного цикла могут быть как движущими, так и силами полезного сопротивления, поэтому работа этих сил за цикл равна нулю. Эти силы считаются внешними силами.
- силы инерции ;
- моменты сил инерции , где m, JS – масса и массовый момент инерции звена; и – линейное и угловое ускорения;
- силы реакций в кинематических парах , возникающие в опорах звеньев и являющиеся внутренними силами для механизма в целом и внешними для каждого отдельного звена.
Необходимо отметить, что под силами понимаются равнодействующие соответствующих распределенных в месте контакта кинематической пары нагрузок. Все вышесказанное относительно сил распространяется и на моменты сил.