Файл: Государственное бюджетное профессиональное образовательное учреждение московский государственный образовательный комплекс.docx

SolidWorks выполняет анализ методом конечных элементов (FEA).

Конструкция портала представлена ​​на рис.2.3.16
Рисунок 2.3.16 – Конструкция портала

Для правильного расчета необходимо правильно определить силы, действующие на балку. Как упоминалось выше, на балку действуют только силы инерции, и влияние ускорений структурных частиц (и сил инерции) на их напряженное состояние можно учесть с помощью принципа Даламбера.

В случае стержневых конструкций и конструкций с постоянным поперечным сечением эту силу можно представить как равномерно распределенную нагрузку на конструкцию Qin.

Сила инерции блока с рабочей жидкостью, действующая на структуру портала, является реальной силой, которая соответствует произведению массы и ускорения блока.

Начальные числа начала моделирования:

- Эквивалентная длина балки: ???? = 1300 мм;

- Ускорение разгона и замедления: ???? = 2 м / с2;

- Вес портала: ????порт = 40кг;

- Масса блока с рабочим органом: ????b = 20 кг;

Представьте себе влияние собственной массы портала как распределенную нагрузку: = 0,0615 Н / мм; и влияние массы блока на тело работы в виде сосредоточенного заряда: ???? = 40 Н.

Максимальная деформация держателя возможна при приложении силы инерции блока рабочей жидкости к центру держателя.



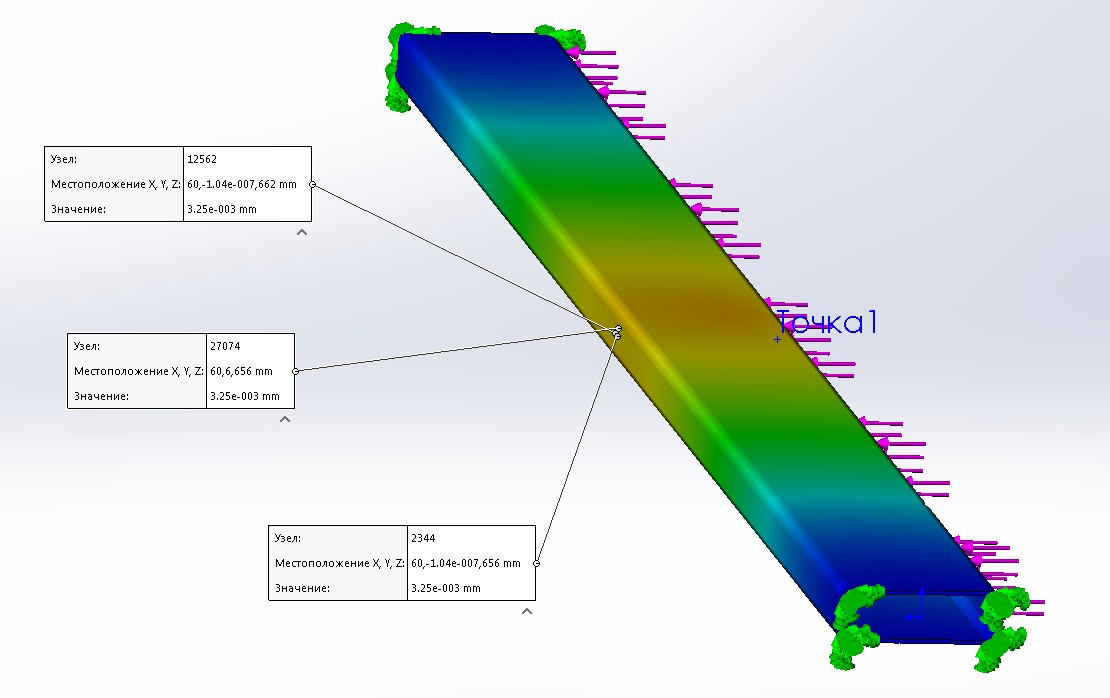
Рисунок 2.3.17 – Результат расчета прогиба балки.

Максимальное значение компенсации f составляет 3,25 * 10-3 мм.

С помощью расчетного программного обеспечения Simulink к трехмерной модели балки были применены нагрузки и граничные условия, и было рассчитано смещение балочной конструкции. Результат расчета показан на рисунке 2.3.19.

Чтобы проверить точность расчета программного комплекса, мы проводим расчет луча аналитически.

Этот вариант нагружения представляет собой статически неопределенную балку со степенью статической неопределенности n = 2. Найдем перемещение точки портала:

3,0 = 3,038 · 10-3 мм;

Разница между результатами расчета МКЭ и аналитического расчета составила 7%. Конечно-элементный анализ достаточно надежен, чтобы его можно было использовать в этих исследованиях.

Для исследуемой установки с рабочей поверхностью 700 мм жесткость двери достаточно высока; При проектировании более крупных систем с длиной двери около трех метров необходимо учитывать не только деформации, но и погрешности, вызванные упругими колебаниями.

---

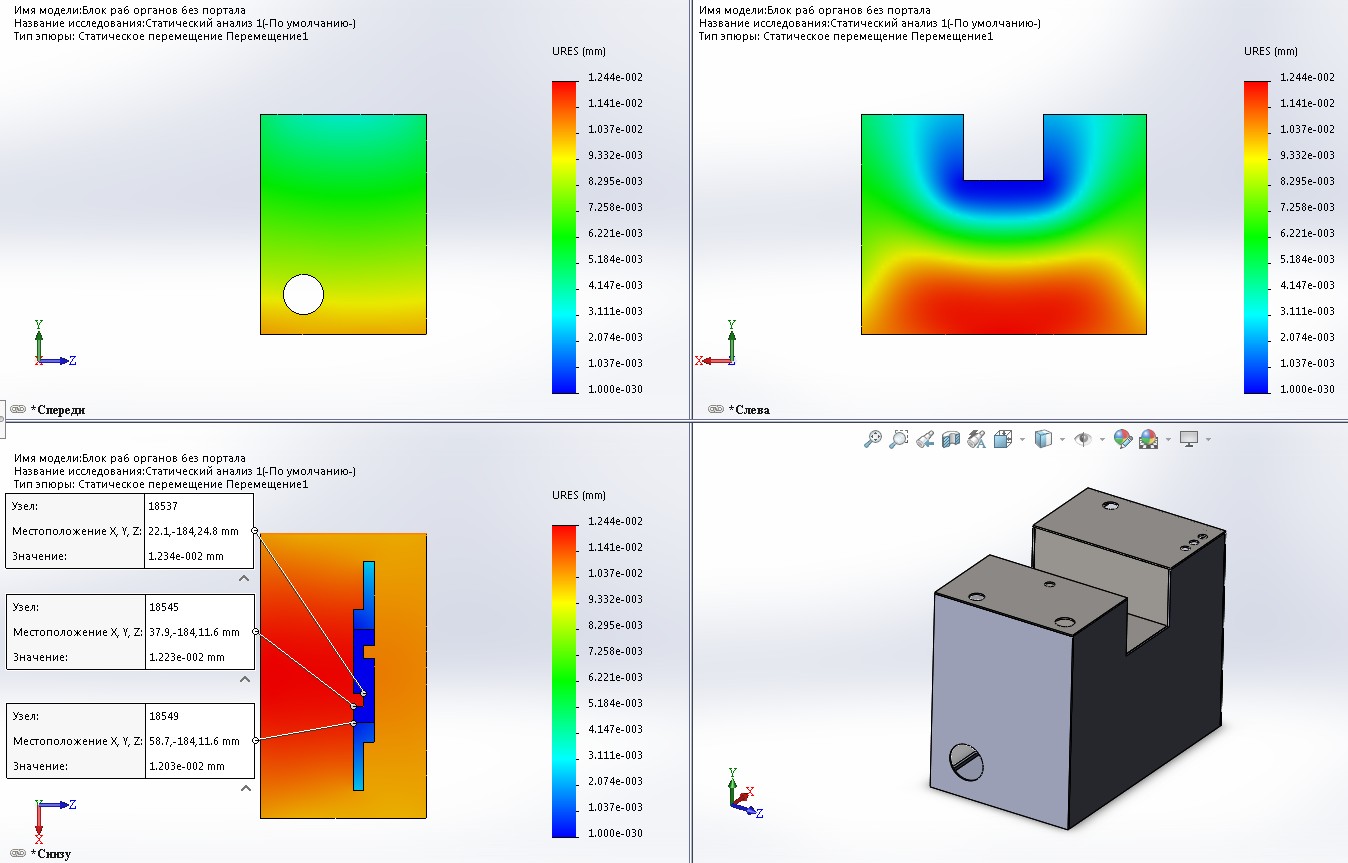
Рисунок 2.3.18 – Результат расчета блока рабочего органа

Исследуем деформацию конструкции блока с рабочим телом под действием сил инерции. Для расчета мы используем программный пакет Simulink. Каждый элемент блочной конструкции воспринимает нагрузку своей массы, которая равномерно распределяется по элементу. Кроме того, опорная плита также воспринимает действие сил инерции прикрепленных к ней элементов: печатающих головок, емкостей с жидким рабочим материалом, электронного управления. Панели, гидравлический контур с рабочим материалом, электромагнитные клапаны.

Условия расчета:

• 
  Машина считается абсолютно жесткой.
  
• 
  Граничное условие - жесткая привязка к вагону;
  
• 
  Ускорение разгона и замедления: ???? = 2 м / с^2;
  

Основание выполнено из алюминиевого сплава, остальные детали - из конструкционной стали.

Максимальное расстояние от материнской платы до места крепления печатающей головки составляет 0,012 мм.

2.4. Математическоемоделированиеструктурыупаковкипесчаногослояпризаданномгранулометрическомсоставе.

Важным аспектом исследования блока аддитивной мехатроники является моделирование структуры покрытия песчаного слоя. Эта информация, вместе с дальнейшими исследованиями, определит наиболее многообещающие области для повышения точности установки мехатронных систем.

В рамках работ было проведено исследование с формовочным песком, который использовался на испытательном стенде ExOne C-15. В данной работе автор определил большое значение морфологии и гранулометрического состава песка для качества получаемых продуктов. В работе показана возможность обмена и замены формовочного материала с целью улучшения параметров рассматриваемой технологии.

Важнейшим параметром при экстракции продуктов любым способом, в том числе с применением аддитивных технологий, является точность, которая зависит от многих параметров, в том числе. Порошковая система.

В этом разделе мы рассмотрим влияние структуры упаковки дисперсных частиц порошковых систем при дозировании материала по принципу «плохого оседания» на точность получаемых продуктов на примере аддитивной мехатронной системы. для производства песка в полимерной форме.

---

При предполагаемой укладке добавки на дверь с помощью виброметра наносится порошок (песочная смесь) с последующим выравниванием шпателем. Дверь приводится в движение ременным приводом.

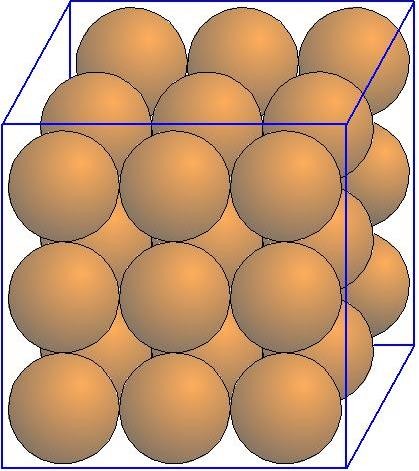
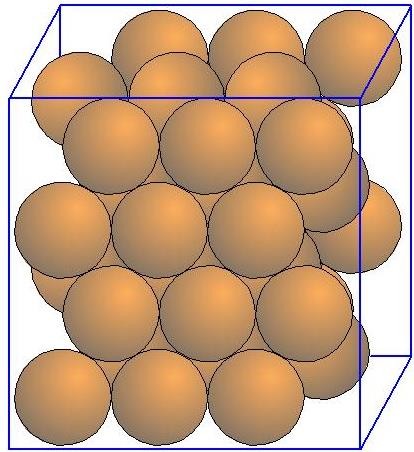Известно, что в однородных монодисперсных порошковых системах сферических частиц существуют два основных типа упорядоченных структур оболочки дисперсных частиц: кубическая (рисунок 2.4.1) с координационным числом 6 и гексагональная (рисунок 2.4.2). При этом плотность заполнения составляет 52,36% и 74% соответственно.

Рисунок 2.4.1 – Кубическая упаковка Рисунок 2.4.2 - Шестиугольная упаковка

Для заказанных типов контейнеров отклонение конечного продукта зависит от номинального значения силы сцепления внешнего слоя частиц. На фиг. 2.4.3 показан общий случай формирования реальных размеров кубической оболочечной конструкции.

Учтите ограничения: если эффект при производстве продукта достаточно сильный (капиллярный эффект для распыления связующего, термический эффект для SLM и SLS), соседние частицы, которые непосредственно примыкают к номинальному размеру продукта, будут сливаться. Это увеличит фактический размер продукта (рисунок 2.4.4). В этом случае разница составляет + 2dp (dp - диаметр частицы). Вторая возможность осуществляется при недостаточно прочном скреплении внешнего слоя частиц, что входит в номинальный размер изделия. В этом случае наблюдается явление «выхода продукта из строя» (рисунок 2.4.5). Максимальное отклонение размера от номинала менее 2 dh.



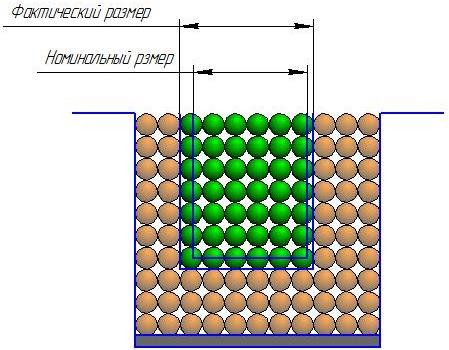
Рисунок 2.4.3 - Общий случай деформации в структуре кубической упаковки



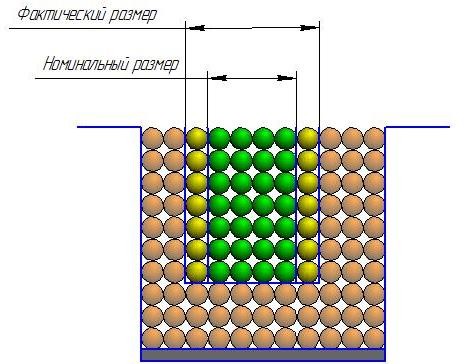
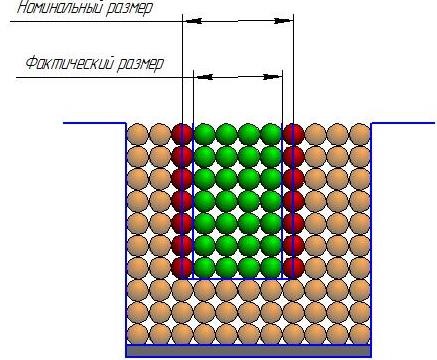
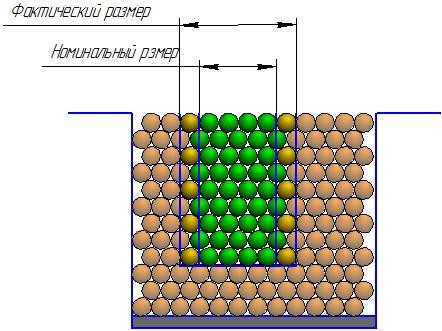Рисунок 2.4.4 - Сильное связывание частиц Рисунок 2.4.5 - Слабое связывание частиц

Рисунок 2.4.6 - Отклонение с гексагональной структурой упаковки

Отклонения размеров изделия от номинальных значений для конструкции шестигранного сопла показаны на рисунке 2.4.6.

---

В случае гексагональной герметизирующей конструкции из-за более плотной структуры и более сильного контакта между частицами (координационное число 12) отклонение от номинального размера происходит только в положительном направлении и составляет от + 1dh до + 2dh.

Истинные порошковые системы полидисперсны с различными модальностями; Структура упаковки этих систем неупорядочена (случайна). Плотность упаковки зависит от физических и механических свойств частиц, их формы и их склонности к агломерации. Чем больше форма частиц отличается от сферической формы и имеет большую угловатость, тем менее плотная структура наполнителя.

Частицы рассеянных реальных материалов обычно имеют разные геометрические формы, отличные от идеальных геометрических тел. В качестве примера на рис. 2.4.7. показана морфология песчинок.

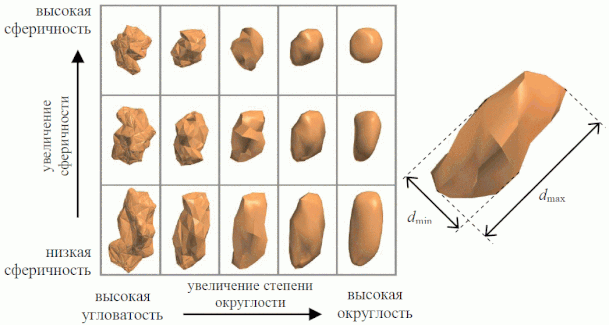
Рисунок 2.4.7 – Морфология зерен песка

Используя инструменты определения веса частицы, результирующую массу можно выразить как массу сферической частицы, которую можно принять во внимание ????_сф.ч. = (⁴)????????³ найдём диаметр сферической частицы (2r - единственный параметр) с той же массой, что и исходная угловая частица. Этот подход известен как теория эквивалентных сфер. При измерении определенных свойств частицы предполагается, что они связаны с эквивалентной сферической частицей, и вычисляется четко определенный параметр (сферический диаметр), который характеризует частицу. Этот пример показывает, что нет необходимости описывать частицу тремя или более числовыми значениями, которые, конечно, более точно характеризуют размер, но являются проблематичными по многим причинам.

Заливка кварцевого песка 1К1О101 по ГОСТ 2138-91 считается порошковой системой. Кварцевый песок - это полидисперсная порошковая система.

Фактическая плотность частиц кварцевого песка составляет 2650 кг / м³, а насыпная плотность составляет 1400 кг / м³, что означает, что плотность естественных отложений составляет 52,8%. По результатам ситового анализа была построена диаграмма гранулометрического состава (рис. 2.6.8), которая показывает, что кварцевый песок имеет режим, соответствующий размеру частиц 100 микрометров. Используя формулы, были рассчитаны стандартные отклонения (RMSD) и среднее арифметическое, и было обнаружено, что отношение RMS к среднему составило 0,45.

---

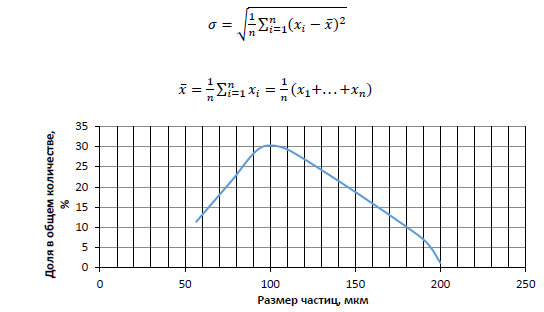
Рисунок 2.4.8 – Дифференциальная диаграмма гранулометрического состава порошка.

---