ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 245
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
необходимо для себя ответить Изучая учебник для конкретного класса, учитель обязан ответить себе на нижеперечисленные вопросы:
Даются ли нам определения?
Понятно ли введены новые определения, объекты, понятия?
К какому типу строения определений мы можем отнести данное нам определение?
Мы работаем с новым типом строения определения или мы уже встречались с ним ранее?
Какие учебные и информативные процессы нам следует выполнить, чтобы раскрыть типы строений определения и как его лучше всего применять?
Каков должен быть наш материал, чтобы была возможность обнаружить все действия и операции?
Рассмотрим логико-математический анализ темы «Многоугольник»
Мы заранее уже знаем цели этой темы:
При помощи логической связи между собой создать структуру определений основных фигур данной темы;
Выявить рациональную сущность определений выпуклого многоугольника, считая ее частью плоскости;
Выявить состав единых математических приемов неполной индукции, которые мы используем для доказательства в теме основных утверждений.
Сгруппировать и подытожить отдельные метрические свойства выпуклых многоугольников.
Теперь приступим к логико-математическому анализу данной темы.
Материал в теме «Площадь многоугольника» представлен на основе дедукции,
так как даются определения всем фигурам, которые вводятся в теме.
В самом начале темы дается определение площади многоугольника, также приводятся условия их существования. Далее приводятся свойства
площадей многоугольников. Из-за большого выражения под корнем и дроби их вычисления представляют некоторую сложность.
В данной теме доказываются следующие теоремы: Площади ромба и трапеции;
Площади треугольника; Площади прямоугольника; Площади параллелограмма;
В основе данных теорем является свойство равного многоугольника,
который имеет равные площади, его используют и при доказательстве.
Опираясь на анализ содержания данного учебного материала, мы можем полагать, что образование нового представления геометрической фигуры, являющейся частью плоскости, и обнаружение метрических и конструктивных свойств на базе решения математических задач, является ведущей учебной задачей данной темы.
Логико-математический анализ определений понятий по теме «Площадь»
Таблица 1
Перед тем как вводить понятие «Площади фигур», эта тема нам представляется синтезом аналитического и традиционно-синтетического метода. Возьмем к примеру площадь треугольника, информация здесь представлена аналитическим способом, а подтверждения применяются традиционно-синтетическим методом.
Когда мы начинаем изучать тему «Площади фигур» воспользуемся такой схемой: простая фигура – величина площади фигуры – площадь параллелограмма – площадь прямоугольника - площадь трапеции – площадь подобных фигур.
 Ученикам показывают готовые чертежи с изображением простых фигур и они должны определить: простую ломаную, простую замкнутую ломаную, замкнутую ломаную, плоский треугольник, выпуклый многоугольник, плоский пятиугольник. Нам важно помнить, что плоский треугольник будет являться конечной частью плоскости, которая ограничена
Ученикам показывают готовые чертежи с изображением простых фигур и они должны определить: простую ломаную, простую замкнутую ломаную, замкнутую ломаную, плоский треугольник, выпуклый многоугольник, плоский пятиугольник. Нам важно помнить, что плоский треугольник будет являться конечной частью плоскости, которая ограничена
треугольником. «Выпуклый многоугольник – это такой многоугольник, который относительно любой прямой лежит в одной, содержащей его сторону. Конечная часть плоскости, которая ограничена многоугольником является плоским многоугольником.»[8, с.228]
«Многоугольник - это за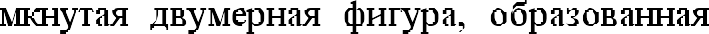
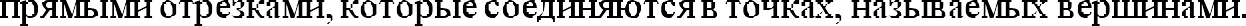
 ,
,
 называется невыпуклым.» [8, С.58]
называется невыпуклым.» [8, С.58]
Если геометрическая фигура мы можем разбить на конечное число плоских треугольников, то она будет являться простой. В качестве примера этой простой фигуры нам послужит плоский выпуклый многоугольник, разбивающий диагоналями на плоские треугольники, которые будут выходить из одной вершины.
Площадь простой фигуры будет обладать следующими свойствами:
единице.»[12]
Аксиоматический подход нам поможет для того, чтобы определить новую величину. Площадь простой фигуры описана свойством аддитивности. При равенстве фигур будут равны и площади, но обратное утверждение не всегда будем правильным.
В курсе арифметики большинство учеников уже успевают знакомиться с формулами площадей некоторых фигур. Измеряя площади при помощи
памяток, ученики знакомятся с ее оценкой по недостатку и по избытку. Таким образом, школьники постепенно готовятся уже к пониманию вывода формулы площади прямоугольника.
Проводя уроки, касающиеся «Площадь фигур», вывод общих формул мы должны закреплять вывод общих формул, рассматривая частные примеры. Теоретический материал должен всячески снижаться, (в разумных пределах) для
Даются ли нам определения?
Понятно ли введены новые определения, объекты, понятия?
К какому типу строения определений мы можем отнести данное нам определение?
Мы работаем с новым типом строения определения или мы уже встречались с ним ранее?
Какие учебные и информативные процессы нам следует выполнить, чтобы раскрыть типы строений определения и как его лучше всего применять?
Каков должен быть наш материал, чтобы была возможность обнаружить все действия и операции?
Рассмотрим логико-математический анализ темы «Многоугольник»
Мы заранее уже знаем цели этой темы:
При помощи логической связи между собой создать структуру определений основных фигур данной темы;
Выявить рациональную сущность определений выпуклого многоугольника, считая ее частью плоскости;
Выявить состав единых математических приемов неполной индукции, которые мы используем для доказательства в теме основных утверждений.
Сгруппировать и подытожить отдельные метрические свойства выпуклых многоугольников.
Теперь приступим к логико-математическому анализу данной темы.
Материал в теме «Площадь многоугольника» представлен на основе дедукции,
так как даются определения всем фигурам, которые вводятся в теме.
В самом начале темы дается определение площади многоугольника, также приводятся условия их существования. Далее приводятся свойства
площадей многоугольников. Из-за большого выражения под корнем и дроби их вычисления представляют некоторую сложность.
В данной теме доказываются следующие теоремы: Площади ромба и трапеции;
Площади треугольника; Площади прямоугольника; Площади параллелограмма;
В основе данных теорем является свойство равного многоугольника,
который имеет равные площади, его используют и при доказательстве.
Опираясь на анализ содержания данного учебного материала, мы можем полагать, что образование нового представления геометрической фигуры, являющейся частью плоскости, и обнаружение метрических и конструктивных свойств на базе решения математических задач, является ведущей учебной задачей данной темы.
Логико-математический анализ определений понятий по теме «Площадь»
Таблица 1
| Название понятия | Вид определения понятия | Название способа представления определения понятия |
| [4, С.2] «Площадь фигуры - это число, показывающее, из скольких единиц площади составляется эта фигура (за единицу площади берется квадрат, сторона которого равна единице длины). Однако такое | [7]«Генетическое определение, то есть такое определение, в котором описывается или указывается способ его образования, возникновения. Генетические определения представляют собой | Аксиоматический способ.[7] «Площадь фигуры - это положительная величина, численное значение которой обладает следующими свойствами: а) равные фигуры имеют равные площади; б) если |
| наглядное пояснение не может служить точным математическим определением понятия площади. Неясно, например, каким образом из единиц площади составляется круг заданного радиуса.»[4, С.2] | разновидность определения через род и видовые отличия.»[7] | фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей; в)площадь квадрата со стороной равной единице измерения равна единице.» [7, С.52] |
§2. Методика введения понятия площади в школьных учебниках по геометрии.
Перед тем как вводить понятие «Площади фигур», эта тема нам представляется синтезом аналитического и традиционно-синтетического метода. Возьмем к примеру площадь треугольника, информация здесь представлена аналитическим способом, а подтверждения применяются традиционно-синтетическим методом.
Когда мы начинаем изучать тему «Площади фигур» воспользуемся такой схемой: простая фигура – величина площади фигуры – площадь параллелограмма – площадь прямоугольника - площадь трапеции – площадь подобных фигур.
 Ученикам показывают готовые чертежи с изображением простых фигур и они должны определить: простую ломаную, простую замкнутую ломаную, замкнутую ломаную, плоский треугольник, выпуклый многоугольник, плоский пятиугольник. Нам важно помнить, что плоский треугольник будет являться конечной частью плоскости, которая ограничена
Ученикам показывают готовые чертежи с изображением простых фигур и они должны определить: простую ломаную, простую замкнутую ломаную, замкнутую ломаную, плоский треугольник, выпуклый многоугольник, плоский пятиугольник. Нам важно помнить, что плоский треугольник будет являться конечной частью плоскости, которая ограниченатреугольником. «Выпуклый многоугольник – это такой многоугольник, который относительно любой прямой лежит в одной, содержащей его сторону. Конечная часть плоскости, которая ограничена многоугольником является плоским многоугольником.»[8, с.228]
«Многоугольник - это за
 называется невыпуклым.» [8, С.58]
называется невыпуклым.» [8, С.58]Если геометрическая фигура мы можем разбить на конечное число плоских треугольников, то она будет являться простой. В качестве примера этой простой фигуры нам послужит плоский выпуклый многоугольник, разбивающий диагоналями на плоские треугольники, которые будут выходить из одной вершины.
Площадь простой фигуры будет обладать следующими свойствами:
-
«Равные фигуры будут иметь равные площади; -
У фигуры, разбитая на части и являющееся простой фигурой, площадь фигуры равна сумме площадей ее частей; -
Площадь квадрата со стороной, равной единице измерения, равна
единице.»[12]
Аксиоматический подход нам поможет для того, чтобы определить новую величину. Площадь простой фигуры описана свойством аддитивности. При равенстве фигур будут равны и площади, но обратное утверждение не всегда будем правильным.
В курсе арифметики большинство учеников уже успевают знакомиться с формулами площадей некоторых фигур. Измеряя площади при помощи
памяток, ученики знакомятся с ее оценкой по недостатку и по избытку. Таким образом, школьники постепенно готовятся уже к пониманию вывода формулы площади прямоугольника.
Проводя уроки, касающиеся «Площадь фигур», вывод общих формул мы должны закреплять вывод общих формул, рассматривая частные примеры. Теоретический материал должен всячески снижаться, (в разумных пределах) для