Файл: ВсяМехЛАБраб2части.doc

20 см – 1 см = 19 см.

Следовательно, далее на отрезке длиной 1,9 см размечаем N делений нониуса, т.е. 10 делений. При этом цена деления шкалы нониуса будет равна по формуле (1):

делений или 1,9 см  Вывод: одно деление нониуса меньше двух делений (деление на нониусе сравнивается с k делениями на основной шкале) основного масштаба на 0,1 см  эта величина и будет точностью измерений на полученном приборе (например, штангенциркуле).

Иначе говоря, по построению имеем: 10 делений нониуса меньше 20 делений масштаба на 1 см, тогда 1 деление нониуса меньше 2 делений масштаба на 1/10 см, при этом разница распределена в пределах между 2-мя этими делениями.

Получается, что проделанные изменения в построении не сказались на величине точности (все также 0,1 см).

Но что же изменилось? Для нахождения ответа изучим рис. 2.

Исходное положение: при совмещении нулей обеих шкал расстояние между рабочими зажимами шкал равно нулю (рис.2а)), 10-е (последнее) деление нониуса совпадает с 19-м делением основной шкалы.

При помещении образца, например болта (рис.2 б)), между зажимами нулевая отметка на нониусе смещается относительно нуля основной шкалы на искомое расстояние. По рисунку видно, что в это расстояние теперь вмещается 3 целых деления масштаба и еще какая-то его часть. Для определения длины этой части ищем номер деления на нониусе, совпавшего с некоторым делением основной шкалы: на рисунку это – 8-ое деление, совпадающее в точности по положению с делением номер 19 на основной шкале.

По аналогии с первым примером мы должны утверждать, что длина искомой части равна 8∙0,1=0,8 см, а измеряемое расстояние 3+0,8=3,8 см.

Однако заметим следующее: соседние с совпавшим делением, а именно 7-е и 9-е деления нониуса отстоят от ближайших делений основной шкалы (соответственно 17-м и 21-м) на 0,1 см. Эти деления – вторые на очереди претендентов на «совпадение». Чтобы совпало какое-либо из этих делений, расстояние между зажимами должно уменьшиться или увеличиться на 0,1. представим же себе ситуацию, что оно уменьшилось лишь на 0,05, т.е. на половину от 0,1 см. Какое же деление нониуса теперь будет совпадающим?

Теперь 8-е деление нониуса будет левее 19 основной шкалы на 0,05 см, а 7-е деление нониуса правее 17-го на такую же величину. При этом истинная длина образца будет 3,75 см, но на данном приборе мы может с имеющейся точностью получить его значение как 3,7 см (примем совпадение на 7-м делении нониуса) или как 3,8 см (если принять совпадающим 8-е). Тогда в обоих случаях будет верно: 3,75=3,7 0,1 и 3,75=3,8 0,1. Полученные значения соответствуют округлению до десятых долей сантиметра, но с недостатком или с избытком.

В заключение подумаем, когда же предпочесть второй способ построения первому?

Разница между ними состоит в «укрупнении» делений шкалы нониуса, по сравнению с делениями основной шкалы.

Поэтому предпочтение второму способу будет отдано скорее всего тогда, когда деления основной шкалы настолько мелки, что построение нониуса с еще более мелкими делениями нецелесообразно из-за возможного возникновения затруднений при снятии показаний, т.е. к возрастанию субъективной погрешности отсчета.

Обобщая проделанное, получаем следующие результаты:

• (2) – точность измерений по шкале с нониусом (штангенциркуля).

В обоих разобранных примерах это была величина .

Следовательно, увеличить точность можно за счет увеличения числа делений на нониусе. Но, не меняя при этом длину основного отрезка (эталона), будем получать одновременное «мельчание» этих делений, что также на определенном пределе становится источником дополнительных трудностей, т.е. не целесообразно.

Таким образом, при создании шкал с нониусом необходимо подбирать оптимальное соотношении основных параметров: длины эталона (числа делений на основной шкале, по сравнению с общей длиной которых длина шкалы нониуса меньше на одно такое деление; в примере 1 – 10 делений, в примере 2 – 20 делений. Иначе, это эквивалентно выбору размеров шкалы нониуса), числа делений шкалы нониуса N (примеры 1 и 2 – 10 делений) и коэффициента кратности k (пример 1: k=1; пример 2: k=2).

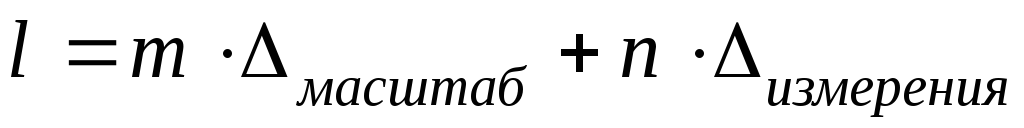• (3) - длина предмета, где m – число полных делений основной шкалы (масштаба) между нулевыми отметками двух шкал, n – порядковый номер совпадающего деления нониуса.

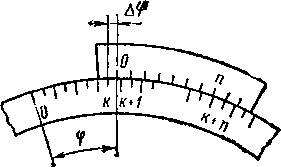
2. Круговой нониус представляет собой дуговую линейку (рис. 3), скользящую вдоль кругового масштаба (лимба), предназна­ченного для измерения углов. Так как длина дуги s окружности радиуса R и центральный угол связаны соотношением

рис. 3

то измерение углов можно заме­нить измерением дуг. В принципе круговой нониус ничем не отли­чается от линейного и для него справедливы те же формулы. Так, для случая кругового нониуса формулу (3) можно записать так: , где— цена деления лимба, m – число полных делений лимба, n – порядковый номер совпадающего деления нониуса.

Штангенциркуль.

Штангенциркуль служит для линейных измерений, не требующих высокой точности. Отсчетным приспособлением у всех конструкций штангенинструментов служат шкала штанги и линейный нониус. Цена деления основ­ной шкалы штанги равна обычно 1 мм. Нониусы штангенциркулей изготавливаются таким образом, что k=1, 2, 5 (см. формулу (1)). Погрешность нониусов обычно равна 0,1; 0,05 или 0,2 мм.

Нониус укреплен в подвижной рамке, скользящей вдоль ос­новной шкалы штанги. При нулевом показании инструмента нуль нониуса совпадает с нулевым штрихом основной шкалы. При измерении детали подвижная рамка 1 с нониусом смещается, и деталь зажимается губками 2 штангенциркуля. Существует несколько видов штангенциркулей. Они отличаются типом и ко­личеством измерительных губок, длиной штанги, типом нониусов или наличием некоторых вспомогательных деталей. При наличии у штангенциркулей верхних 3 и нижних 2 измерительных губок, его можно применить как для внутренних измерений, так и для внешних. Часто штангенциркуль снабжается линейкой 4, служа­щей для измерения глубин.

Микрометр.

Для более точных измерений применяют микрометрические инструменты. Они бывают нескольких типов: микрометр для наружных измерений, микрометрический глуби­номер и микрометрический нутромер.

• М

  рис.4

  икрометр для наружных измерений (рис. 4) состоит из по­лого стержня, жестко соединенного со скобой. В полость стержня ввинчен микрометрический винт. При измерении предмет зажи­мается между неподвижным стержнем 2 и подвижным торцом мик­рометрического винта 3. Микровинт вращают, держась за трещот­ку 4 (в более совершенных микрометрах момент соприкосновения мик­рометрического винта с измеряемой поверхностью фиксируется по шкале чувствительного динамометра, укрепленной в скобе); вместе с микровинтом вращается корпус барабана 1, переме­щаясь при этом поступательно относительно стержня. Отсчет ве­дется по горизонтальной шкале, нанесенной на полый стержень, и по шкале барабана. Отсчетное устройство микрометра состоит из двух шкал. Горизонтальная шкала стержня представляет собой двойную шкалу с ценой деления 0,5 мм, нанесенную по обе стороны продольной черты таким образом, что верхняя сдвинута относительно нижней на половину деления. Цена деления шкалы барабана может быть установлена следующим образом: пусть число делений круговой шкалы барабана n=50. Шаг микровинта h =0,5 мм. Следовательно, одному полному обороту микровинта (и барабана) соответствует линейное перемещение края барабана на 0,5 мм. Цена деления круговой шкалы

Отсчет производится следующим образом: по горизонтальной шкале стержня отсчитывается размер измеряемого предмета с точностью до 0,5 мм. Сотые доли миллиметра отсчитываются по круговой шкале барабана. Полу­ченные результаты складываются. Число сотых долей соответствует делению шкалы, расположенному против продольной черты на стер­жне. Порядок отсчета одинаков для всех типов микрометриче­ских инструментов. Микрометры изготовляются с пределами изме­рений 0-25, 50, 75 мм и т.д., до 1600 мм. Увеличение пределов измерений достигается увеличе­нием размера скобы.

Содержание экспериментальных заданий

Задание 1. Рассчитайте точность имеющихся в лаборатории шкал с нониусами (различных штангенциркулей) и сравните свои расчеты с отметками на самих приборах.

Задание 2. Постройте шкалу с нониусом, точность которой будет 1 мм (0,5 мм, 0,25 мм, 0,05 мм), считая что основная шкала имеет деления ценой 1 мм. В каждом случае укажите выбранные вами значения трех рассмотренных выше параметров таких шкал.

Задание 3. Для имеющихся твердых тел измерить соответствующие линейные размеры. Вычислить их площади поверхности и объемы и рассчитать погрешности полученных результатов как косвенных измерений.

Часть Первая

Лабораторная работа № 1.1.

Определение плотности тел, имеющих правильную

геометрическую форму.

Цель работы: научиться проводить прямые и косвенные измерения физических величин (масса, длина, объем, плотность) и оценивать погрешность полученных результатов; познакомиться с некоторыми источниками погрешностей при измерении плотности тел в воздухе.

Приборы и принадлежности: штангенциркуль, микрометр, технические весы, разновесы, исследуемые образцы.

Краткая теория вопроса и метода.

Рассмотрим понятие плотности тела. Мы находим ее, определив массу рассматриваемого тела m и его объем V, как частное (1). Но если тело неоднородное (в обычном смысле этого слова), тоесть так называемая «средняя плотность». Вырезая из разных мест рассматриваемого тела 2 малых куска, мы в этом случае найдем, что плотности их различны. Если кусок настолько мал, что для каждой его половины мы находим одну и ту же плотность, то мы говорим, что нашли истинную плотность тела в той его точке, около которой вырезан данный кусок. Такое утверждение будет тем более определенным, чем меньше вырезанный кусок. Таким образом, плотность тела – дифференциальная характеристика распределения вещества по объему тела, т.е. приходим к определению:(2) или, где-физически малый объем. А также стремление объема под знаком предела к нулю не следует понимать в математическом смысле! В самом деле, последовательно уменьшая объем V, мы придем к таким объемам, которые заключают немного, а может даже и 1 атом; при дальнейшем разделении таких объемов пополам может оказаться, что в одной половине, скажем, 3, а в другой 5 атомов (потому хотя бы, что вследствие тепловых движений атомы распределились по объему на мгновение неравномерно). Очевидно, поэтому, что постепенное уменьшение V в формуле (2) на опыте сначала будет давать постепенное приближение к какой-то предельной величине , а при дальнейшем делении разбросы значенийбудут расти, и формула (2) потеряет физический смысл. Поэтому для тех определений плотности, которые обычно нужны инженеру и физику, нам надо пользоваться не «математическим», а «физическим» пределом, т.е. предполагать уменьшениеV не до нуля, а до некоторого «разумного» предела. Подобные рассуждения относятся и к весьма многим другим физическим понятиям.

Масса тела характеризует количество заключенной в теле материи. Масса тела не зависит от того, где находится это тело, так как количество вещества в теле не может измениться от перемены места.