Файл: ВсяМехЛАБраб2части.doc

6) Отметить на оси абсцисс середину стержня и провести через эту точку прямую, параллельную оси ординат. В итоге получится график, показанный на рис.5.

7. По графику определить для 5 различных значения периода соответствующие им значений приведенной длины маятника L, см. ф-лу (15). Для этого нужно провести 5 прямых, параллельных оси абсцисс так, чтобы каждая прямая пересекала построенную кривую в двух точках. Значения Т и L , определенные для каждой такой прямой, записать в табл. 2.

8. По формуле (16) вычислить g для каждого измерения и найти среднее значение

9. Вычислить абсолютную и относительную погрешность по формулам

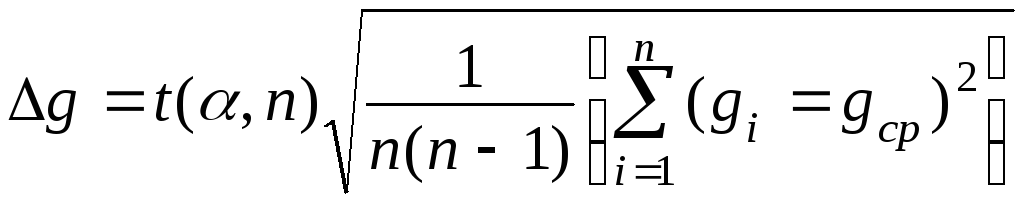
 Таблица 2.

где t(a,n) - коэффициент Стъюдента,

.

10) Записать конечный результат в виде

g =..... ±.......

11) Сформулировать вывод о точности косвенных методов измерения ускорения свободного падения, опробированных в работе.

Вопросы к отчету.

1. Какие колебания называются гармоническими? Дать определение их основных характеристик (амплитуды, фазы, периода, частоты, циклической частоты).

2. При каких условиях колебания физического маятника можно считать гармоническими?

3. Вывести формулу периода колебаний физического маятника.

4. Что называется приведенной длиной физического маятника?

5. Что называется моментом инерции материальной точки? Как вычислить момент инерции твердого тела? Сформулировать теорему Штейнера.

6. Вывести расчетную формулу.

7. Почему для определения g не пользуются непосредственно формулой периода колебаний маятника?

Лабораторная работа № 2.6.

Определение ускорения свободного падения с помощью математического маятника.

Цель работы: исследование свойств математического маятника и экспериментальное определение ускорения свободного падения.

Приборы и принадлежности: математический маятник, линейка, секундомер.

Краткая теория вопроса.

Важным видом движения является движение колебательное, т.е. периодическое или повторяющееся. Простейшим периодическим изменением служат гармонические колебания.

Опр.1 Гармоническим колебанием фи­зической величины х называется процесс изменения ее во времени t no закону (1), где А – амплитуда колебания (максимальное значение величиных), Т — период колебания. Величина носит название фазы, - начальная фаза.

Г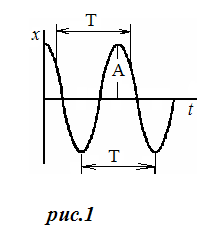рафик такого колебания представлен на рис. 1.

Из определения гармонического колебания следует, что период колебания является наименьшим промежутком времени, по исте­чении которого движение в точности повторяется. Действительно,

За время t=T совершается одно полное колебание. Амплитуда коле­бания А равна максимальному зна­чению х. Величина соответствует фазе в начальный момент времени (t=0) и называется начальной фазой.

Величина (2) называетсякруговой (циклической) частотой. Если начальная фаза равна , то уравнение гармонического колебания записывается в виде: (1’).

Опр. 2 Математическим маятником назы­вается колебательная система, состоящая из материальной точки, прикрепленной к концу идеально гибкой, нерастяжимой и невесо­мой нити, второй конец которой закреплен неподвижно.

Близким к математическому маятнику является тяжелый ша­рик, подвешенный на длинной тонкой нити (рис.2).

Р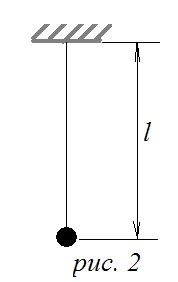ассмотрим основы динамики колебательного движения.

Сила, пропорциональная смещению тела и направленная к положения равновесия, возникает при растяжении (или сжатии) упругой пружины. Поэтому сила, описываемая выражением (3) (закон Гука), называетсяупругой силой.

Опр.2 Сила иного происхождения, обнаруживающая такую же закономерность (3), т.е. пропорциональная отклонению от положения равновесия и при любом положении тела направленная к положения равновесия (возвращающая сила), независимо от ее природы называется квазиупругой.

Система, в которой действует квазиупругая сила с коэффициентомk, обладает потенциальной энергией: (4).

Уравнение движения тела с массой m под действием квазиупругой силы имеет вид: (5).

Его решением будет (1’) при условии  (6).

Таким образом, частота гармонического колебания зависит только от свойств системы (упругости и массы), но не от амплитуды. Амплитуда колебаний определяется не свойствами самой системы, а начальными условиями – энергией, переданной системе в результате начального «толчка».

Рассмотрим колебательное движение математического маятника.

При отклонении от вертикали на угол  система получает потенциальную энергию U=mgh.

Из рис. 3 по теореме Пифагора для прямоугольного треугольника имеем: . При малых углах отклонения величинаh²<<1 и ею можно пренебречь. Тогда получаем:  (7).

Сравнивая (4) и (7)  (8). Тогда:

(9) – не зависит от массы груза!

Возвращающей силой в случае математического маятника служит составляющая силы натяжения нити:

формула (8).

Следовательно, сила - квазиупругая сила с коэффициентом упругости.