ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.04.2024
Просмотров: 418
Скачиваний: 0
СОДЕРЖАНИЕ
Основные теоретические сведения
Краткая теория вопроса и метода.
Описание метода гидростатического взвешивания.
Краткая теория вопроса и метода измерения.
Краткая характеристика методов.
Описание экспериментальной установки.
Краткое знакомство и машиной Атвуда.
Описание прибора и теория метода.
Алгоритм обработки результатов многократных измерений.
Вопросы к отчету:
Какие методы взвешивания вам известны? Чем они отличаются друг от друга? Что служит причиной выбора того или иного метода взвешивания?
Каким методом взвешивания пользовались вы в работе при определении массы исследуемого тела?
Каковы общие правила пользования весами.
Как вы определяли объем тела и какова погрешность полученного значения?
Какие источники погрешностей результата измерения массы данного тела были вами учтены при его взвешивании?
Как была сделана вами поправка на взвешивание в воздухе?
Какова абсолютная погрешность в определении массы тела, получаемая от пренебрежения объемом гирь?
Где и каким образом использовалось в работе предположение об однородности исследуемого образца?
Плотности какого вещества соответствует полученное вами значение плотности выбранного для исследования тела?
Лабораторная работа № 1.2.
Определение плотности твердых тел, имеющих неправильную геометрическую форму методом гидростатического взвешивания.
Цель работы: познакомиться с методом гидростатического взвешивания тел, научиться проводить учет влияния архимедовой силы в воздухе на результаты взвешивания тел на рычажных весах; сформировать умение измерения плотности тел неправильной геометрической формы данным методом и оценки соответствующей погрешности результата.
Приборы и принадлежности: штангенциркуль, технические весы, разновесы, стакан, подставка-скамеечка, нить, исследуемые образцы, вода, термометр, справочная таблица плотности воды при разной температуре.
Краткая теория вопроса.
Рассмотрим понятие
плотности
тела. Мы
находим ее, определив массу рассматриваемого
тела m
и его объем V,
как частное
![]() (1). Но если тело неоднородное (в обычном
смысле этого слова), то
(1). Но если тело неоднородное (в обычном
смысле этого слова), то![]() есть так называемая «средняя плотность».
Вырезая из разных мест рассматриваемого
тела 2 малых куска, мы в этом случае
найдем, что плотности их различны. Если
кусок настолько мал, что для каждой его
половины мы находим одну и ту же
плотность, то мы говорим, что нашли
истинную плотность тела в той его точке,
около которой вырезан данный кусок.
Такое утверждение будет тем более
определенным, чем меньше вырезанный
кусок. Таким образом, плотность тела –
дифференциальная характеристика
распределения вещества по объему тела,
т.е. приходим к определению:
есть так называемая «средняя плотность».
Вырезая из разных мест рассматриваемого
тела 2 малых куска, мы в этом случае
найдем, что плотности их различны. Если
кусок настолько мал, что для каждой его
половины мы находим одну и ту же
плотность, то мы говорим, что нашли
истинную плотность тела в той его точке,
около которой вырезан данный кусок.
Такое утверждение будет тем более
определенным, чем меньше вырезанный
кусок. Таким образом, плотность тела –
дифференциальная характеристика
распределения вещества по объему тела,
т.е. приходим к определению:![]() (2) или
(2) или![]() ,
где
,
где![]() -физически
малый объем. А также стремление объема
под знаком предела к нулю не следует
понимать в математическом смысле! В
самом деле, последовательно уменьшая
объем V,
мы придем к таким объемам, которые
заключают немного, а может даже и 1 атом;
при дальнейшем разделении таких объемов
пополам может оказаться, что в одной
половине, скажем, 3, а в другой 5 атомов
(потому хотя бы, что вследствие тепловых
движений атомы распределились по объему
на мгновение неравномерно). Очевидно,
поэтому, что постепенное уменьшение V
в формуле (2) на опыте сначала будет
давать постепенное приближение к
какой-то предельной величине
-физически
малый объем. А также стремление объема
под знаком предела к нулю не следует
понимать в математическом смысле! В
самом деле, последовательно уменьшая
объем V,
мы придем к таким объемам, которые
заключают немного, а может даже и 1 атом;
при дальнейшем разделении таких объемов
пополам может оказаться, что в одной
половине, скажем, 3, а в другой 5 атомов
(потому хотя бы, что вследствие тепловых
движений атомы распределились по объему
на мгновение неравномерно). Очевидно,
поэтому, что постепенное уменьшение V
в формуле (2) на опыте сначала будет
давать постепенное приближение к
какой-то предельной величине
![]() ,
а при дальнейшем делении разбросы
значений
,
а при дальнейшем делении разбросы
значений![]() будут расти, и формула (2) потеряет
физический смысл. Поэтому для тех
определений плотности, которые обычно
нужны инженеру и физику, нам надо
пользоваться не «математическим», а
«физическим» пределом, т.е. предполагать
уменьшениеV
не до нуля, а до некоторого «разумного»
предела. Подобные рассуждения относятся
и к весьма многим другим физическим
понятиям.
будут расти, и формула (2) потеряет
физический смысл. Поэтому для тех
определений плотности, которые обычно
нужны инженеру и физику, нам надо
пользоваться не «математическим», а
«физическим» пределом, т.е. предполагать
уменьшениеV
не до нуля, а до некоторого «разумного»
предела. Подобные рассуждения относятся
и к весьма многим другим физическим
понятиям.
Масса тела характеризует количество заключенной в теле материи. Масса тела не зависит от того, где находится это тело, так как количество вещества в теле не может измениться от перемены места.
Величина массы
может быть определена по различным ее
проявлениям (инерция, тяготение) путем
сравнения с массой эталонного тела,
произвольно принятой за единицу. Масса
тела связана с весом этого тела
соотношением
![]() ,
гдеg
– ускорение силы тяжести в данной точке
земной поверхности. Вес тела численно
равен силе притяжения тела к Земле без
величины центробежной силы:
,
гдеg
– ускорение силы тяжести в данной точке
земной поверхности. Вес тела численно
равен силе притяжения тела к Земле без
величины центробежной силы:
![]() (3).
Вес тела на различных широтах имеет
разное значение (на экваторе вес тела
- наименьший). Кроме того, вес тела
зависит и от высоты над поверхностью
Земли. Поэтому величины масса и вес
тела существенно
различны.
(3).
Вес тела на различных широтах имеет
разное значение (на экваторе вес тела
- наименьший). Кроме того, вес тела
зависит и от высоты над поверхностью
Земли. Поэтому величины масса и вес
тела существенно
различны.
Принцип взвешивания на весах.
Н
 епосредственно
сила притяжения к Земле может быть
определена при помощи пружинных весов
на основе закона Гука:
епосредственно
сила притяжения к Земле может быть
определена при помощи пружинных весов
на основе закона Гука: - абсолютное удлинение пружины
пропорционально весу тела. Остается
проградуировать шкалу в единицах веса
(массы). Но так как вес основного
платинового эталона в Париже, т.е. на
широте в 450,
принят за единицу веса (1 кГ),
то вес этого же эталона экваторе
окажется меньше, чем 1 кГ,
а на полюсе больше, чем 1 кГ.
- абсолютное удлинение пружины
пропорционально весу тела. Остается
проградуировать шкалу в единицах веса
(массы). Но так как вес основного
платинового эталона в Париже, т.е. на
широте в 450,
принят за единицу веса (1 кГ),
то вес этого же эталона экваторе
окажется меньше, чем 1 кГ,
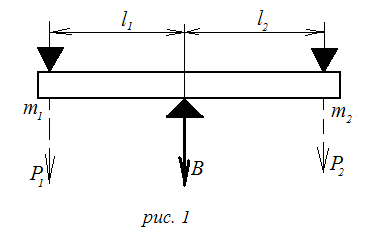
а на полюсе больше, чем 1 кГ.Для сравнения и измерения масс употребляются рычажные весы. Они представляют собой рычаг первого рода (рис.1), в котором расстояния от точек приложения сил до точек опоры равны друг другу (равноплечий рычаг). Поместим на левую чашку весов тело массой m1.
Для того, чтобы
восстановить равновесие, нужно на
правую чашку накладывать разновесы до
тех пор, пока стрелка В не вернется в
первоначальное положение (m2
– масса разновесов). На основании
правила моментов сил
![]() ,
гдеР1
и Р2
соответственно веса тел – силы,
действующие на левую и правую части
рычага в точках опоры чашек весов,
,
гдеР1
и Р2
соответственно веса тел – силы,
действующие на левую и правую части
рычага в точках опоры чашек весов,
![]() и
и![]() - расстояния от этих точек до точки
опоры коромысла. Так как весы равноплечие,
то
- расстояния от этих точек до точки
опоры коромысла. Так как весы равноплечие,
то![]() =
=![]() и при равновесииР1
= Р2.
Но
и при равновесииР1
= Р2.
Но
![]() и
и![]()
![]() .
.
Таким образом, при взвешивании тел на рычажных весах мы сравниваем силу, с которой масса взвешиваемого тела притягивается к Земле, с силой притяжения к Земле эталонной массы. Так как эталоном при этом является масса, то фактически взвешивание на рычажных весах сводится к определению массы.
Так как в любой точке земной поверхности веса тел пропорциональны их массам, а величина g является величиной постоянной, то масса тела однозначно определяет его вес. В этом смысле операцию сравнивания масс, выполняемую на рычажных весах, можно назвать взвешиванием.
Подводя итог сказанному. Видим:
- рычажные весы дают возможность измерить массу тела;
- пружинные весы дают возможность измерить вес тела;
- на широте в 450 и уровне моря результат измерения массы рычажными весами (в кг) и результат измерения веса пружинными весами (в кГ) совпадаю численно. На других широтах и на различных высотах над уровнем моря эти результаты не совпадают.
Методы взвешивания. На практике очень трудно изготовить весы так, чтобы они были строго равноплечими. При взвешивании на неравноплечих весах вес гирь не равен весу тела. Однако существуют различные методы взвешивания, позволяющие определить вес тела достаточно точно.
Метод двойного взвешивания (метод Гаусса) заключается в том, что тело взвешивают 2 раза – один раз на левой чашке, другой раз на правой. искомая масса:
![]() (4),
(4),
т.к.
![]() .
Разложение произведено по формуле
бинома Ньютона.
.
Разложение произведено по формуле
бинома Ньютона.
Метод тарирования (метод Борда). На одну из чашек весов помещают взвешиваемое тело, на другую – любую тару (песок, дробь), которую изменяют до тех пор, пока весы не придут в равновесие. Снимают тело с чашки и накладывают на нее разновесы, пока весы не придут в равновесие. В этом случае вес разновесов равен весу тела. При \том методе влияние неравенства плеч коромысла будет устранено, а точность взвешивания будет лежать в пределах чувствительности весов.
Метод постоянной нагрузки (метод Менделеева). Он позволяет производить взвешивание, не изменяя чувствительности весов. На левую чашку весов помещают гирю предельного веса (например, 100 г), а на правую – мелкие разновесы, общий вес которых равен весу гири. Тело помещают на правую чашку и снимают с нее разновесы до уравновешивания весов. Очевидно, вес тела равен весу снятых гирь. Еще одна выгода метода: он требует каждый раз только одного взвешивания, следовательно, сокращает время и уменьшает погрешность, могущую происходить от многократного взвешивания.
Разновес – набор гирь (тел, служащих для измерения массы), составленный по определенной системе.
При взвешивании
тела трудно подобрать гири так, чтобы
положение равновесия стрелки совпало
с нулевой точкой ненагруженных весов.
Цена деления весов определяется весом
перегрузка, вызывающего смещение
стрелки весов на 1 деление шкалы:
![]() ,
гдеn1
и n2
- число делений у равновесного положения
стрелки до и после нагружения чашки
весов перегрузком.
,
гдеn1
и n2
- число делений у равновесного положения
стрелки до и после нагружения чашки
весов перегрузком.
Тогда при ненулевом
положении стрелки в момент взвешивания,
масса тела будет равна:
![]() (5).
(5).
Итак, определение массы тела может быть произведено путем его взвешивания, но только в том случае, если взвешивание произведено в пустоте или введена соответствующая поправка на кажущуюся потерю веса тела в воздухе.
Поправка на потерю веса тела в воздухе. Все предыдущие рассуждения относились к взвешиванию тел в пустоте. При взвешивании в воздухе на тела и гири действует архимедова выталкивающая сила. Так как объемы взвешиваемых тел и гирь, как правило, неодинаковы, то неодинаковы и выталкивающие силы.
Рассмотрим условие
равновесия при взвешивании в воздухе.
Прежде введем обозначения:
![]() - плотность взвешиваемого тела,
- плотность взвешиваемого тела,![]() - значение плотности, определенное в
воздухе, т.е.
- значение плотности, определенное в
воздухе, т.е.![]() ,
,![]() г/см3
- плотность воздуха,
г/см3
- плотность воздуха,
![]() - объем тела,
- объем тела,![]() - суммарный объем разновесов,
- суммарный объем разновесов,![]() - истинная масса тела (равная массе гирь
при взвешивании в вакууме),
- истинная масса тела (равная массе гирь
при взвешивании в вакууме),![]() - суммарная масса разновесов.
- суммарная масса разновесов.
Пусть на одной
чашке весов находится тело массой
![]() ,
приведем весы в равновесие с помощью
разновесов общей массой
,
приведем весы в равновесие с помощью
разновесов общей массой![]() .
Равновесие весов означает, что на каждое
коромысло действуют равные силы
(равноплечие весы), т.е. получаем с учетом
силы Архимеда в воздухе:
.
Равновесие весов означает, что на каждое
коромысло действуют равные силы
(равноплечие весы), т.е. получаем с учетом
силы Архимеда в воздухе: