ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.04.2024
Просмотров: 422
Скачиваний: 0
СОДЕРЖАНИЕ
Основные теоретические сведения
Краткая теория вопроса и метода.
Описание метода гидростатического взвешивания.
Краткая теория вопроса и метода измерения.
Краткая характеристика методов.
Описание экспериментальной установки.
Краткое знакомство и машиной Атвуда.
Описание прибора и теория метода.
Алгоритм обработки результатов многократных измерений.
Содержание экспериментальных заданий.
Задание 1. Наблюдение стробоскопического эффекта и проверка условия его наступления.
По техническим данным установить пределы изменения частоты вращения мотора (полный диапазон).
Выбрать границы рабочего диапазона, взяв в качестве ограничений наименьшую и наибольшую частоту вспышек стробоскопа.
Подготовить к работе экспериментальную установку согласно рис.1.
Установить частоту вращения мотора из последней трети рабочего диапазона. Примерно, по напряжению на ЛАТРе.
На стробоскопе, начиная с наибольшего значения частоты, плавно изменяйте частоту вспышек и отмечайте в тетради ее значения, при которых наблюдался стробоскопический эффект. Сравните качество наблюдаемой зрительно картины в разных случаях.
Установите, если возможно, наибольшее значение
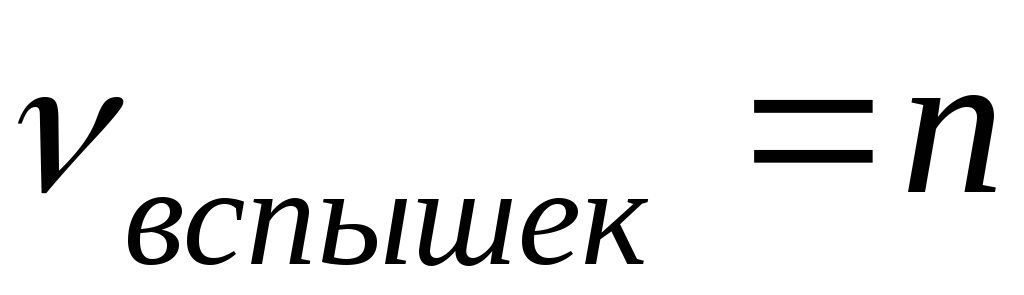 ,
а для других записанных значений
,
а для других записанных значений указать величину коэффициента кратности.
указать величину коэффициента кратности.В случае, когда установить значение
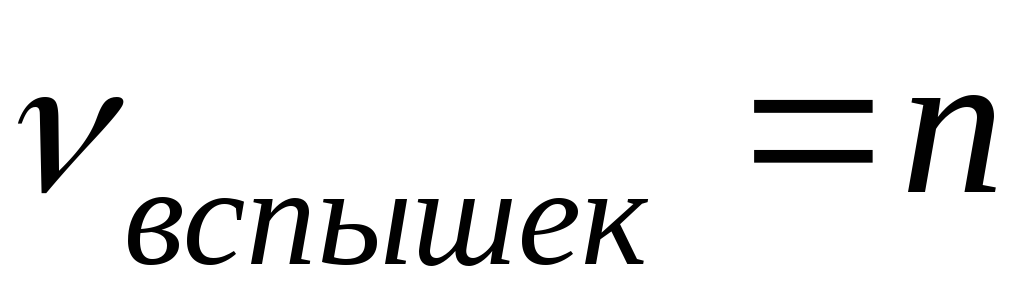 не удается (создается впечатление
возможности очередного наблюдения
эффекта остановки при дальнейшемувеличении
частоты вспышек, что невозможно)
проделайте, начиная с п. 3), задание 1
заново, но для меньшего, чем в первый
раз, значения напряжения на ЛАТРе.
не удается (создается впечатление
возможности очередного наблюдения
эффекта остановки при дальнейшемувеличении
частоты вспышек, что невозможно)
проделайте, начиная с п. 3), задание 1
заново, но для меньшего, чем в первый
раз, значения напряжения на ЛАТРе.Вычислить
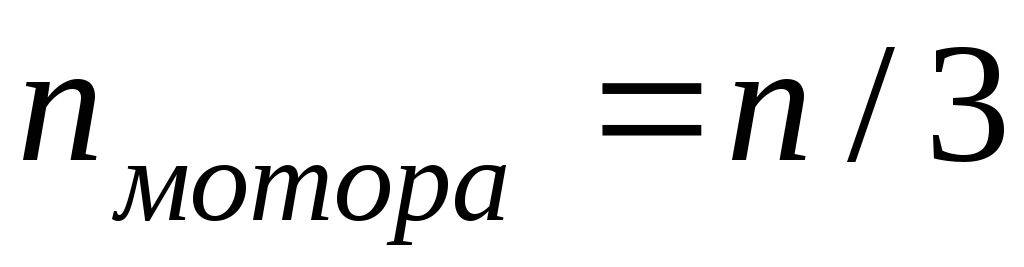 .
Сравнить полученные данные с расчетами
из пункта 1) этого задания. Сделать
соответствующий вывод.
.
Сравнить полученные данные с расчетами
из пункта 1) этого задания. Сделать
соответствующий вывод.
Задание 2. Определение периода вращения электромотора (диска).
Подготовить к работе экспериментальную установку согласно рис.1.
Установить работу двигателя с помощью ЛАТРа (по показаниям величины напряжения
 )
нанекоторую
скорость вращения
в пределах
первой половины от всего диапазона
возможных скоростей его вращения.
Отметить и записать выбранное значение
)
нанекоторую
скорость вращения
в пределах
первой половины от всего диапазона
возможных скоростей его вращения.
Отметить и записать выбранное значение
 напряжения на ЛАТРе.
напряжения на ЛАТРе.Включить стробоскоп и выбрать первый поддипазон частот его вспышек (изменять поддиапазон можно в соответствии с целью пункта 5) этого задания!).
Плавным вращение ручки регулятора частоты вспышек на стробоскопе добиться кажущейся остановки вращения диска. После чего снять соответствующее показание частоты вспышек
 .
.Определить частоту
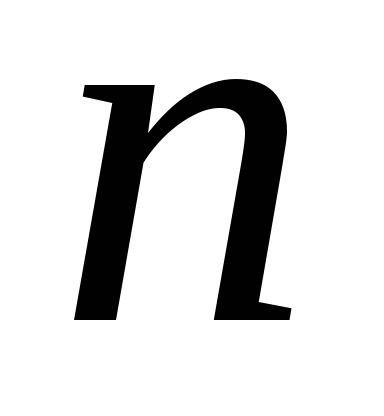 смены секторов, а соответственно и
частоту вращения мотора (не изменяя
его скорости, т.е. напряжение на ЛАТРе
все время должно быть неизменным!):
смены секторов, а соответственно и
частоту вращения мотора (не изменяя
его скорости, т.е. напряжение на ЛАТРе
все время должно быть неизменным!): .
Т.е. установить и экспериментально
доказать значение коэффициента
кратности частот
.
Т.е. установить и экспериментально
доказать значение коэффициента
кратности частот .
.Вычислить период
 (вс)
и угловую скорость
(вс)
и угловую скорость
 вращения мотора (врад/с)
соответственно по формулам:
вращения мотора (врад/с)
соответственно по формулам:
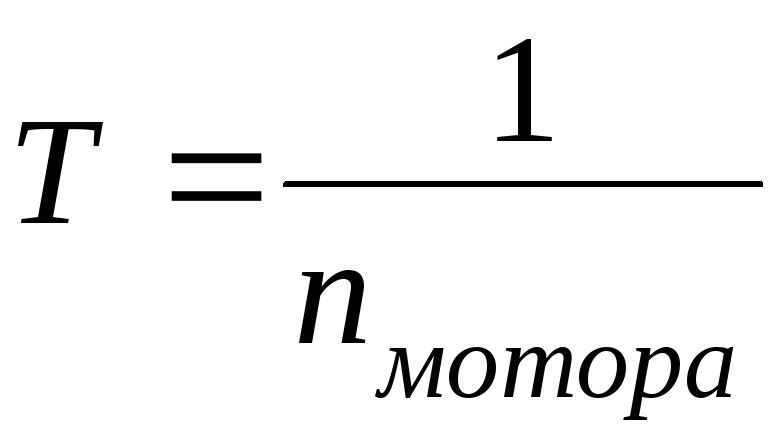 и
и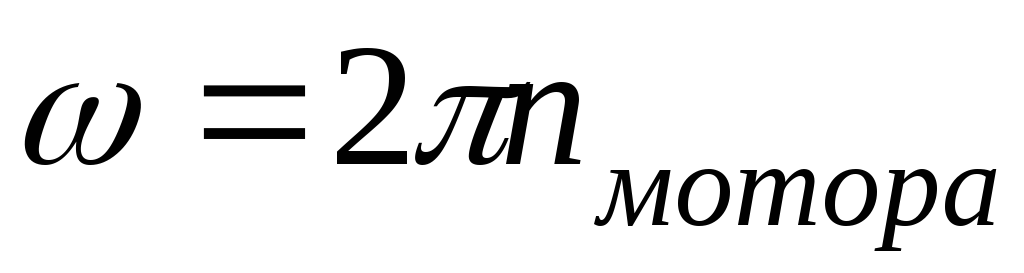 .
.-
Записать полученные значения в первую строку данных таблицы 1.
№ п/п
u, В
 ,
Гц
,
Гц ,
Гц
,
Гц ,
об/с
,
об/с ,
об/с
,
об/с ,
с
,
с ,
рад/с
,
рад/с1.
...
5-7
Вычислить абсолютную
 и относительную
и относительную погрешность полученного значения
угловой скорости вращения диска.
погрешность полученного значения
угловой скорости вращения диска.
Задание 3. Построение графика зависимости скорости вращения мотора от напряжения на ЛАТРе.
После выполнения задания 2 изменить напряжение на ЛАТРе на величину
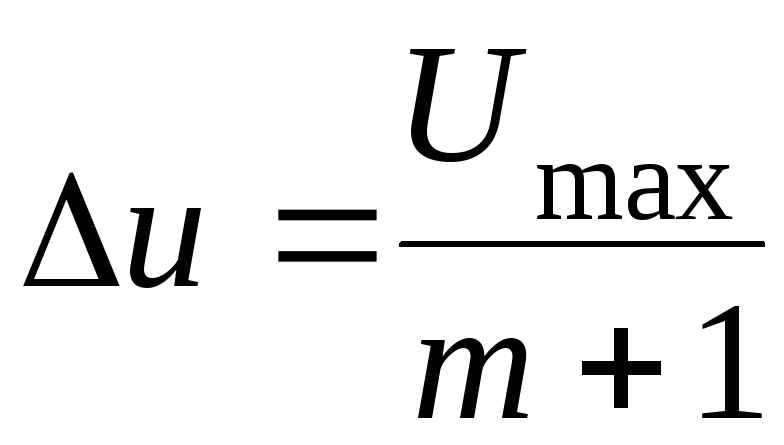 ,
где
,
где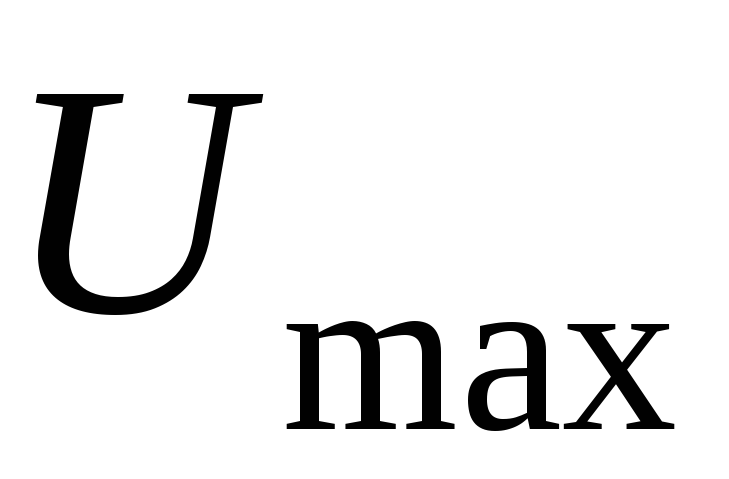 - наибольшее значение напряжения на
ЛАТРе, при котором диск не слетает с
оси мотора (т.е. в пределах возможности
наблюдения),
- наибольшее значение напряжения на
ЛАТРе, при котором диск не слетает с
оси мотора (т.е. в пределах возможности
наблюдения),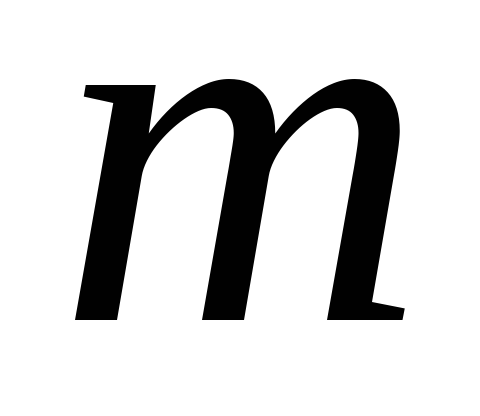 - полное количество опытов, которые вы
хотите провести в рамках этого задания
(число строк данных в первом столбце
таблицы 1, т.е. по выбору одно из значений
5, 6 или 7). Иначе можно поступить проще:
провести измерения при следующих
значениях напряжения на ЛАТРе: 40, 60,
80, 100 и 120 В. Шаг изменения напряжения
также можно менять в случае необходимости.
- полное количество опытов, которые вы
хотите провести в рамках этого задания
(число строк данных в первом столбце
таблицы 1, т.е. по выбору одно из значений
5, 6 или 7). Иначе можно поступить проще:
провести измерения при следующих
значениях напряжения на ЛАТРе: 40, 60,
80, 100 и 120 В. Шаг изменения напряжения
также можно менять в случае необходимости.Проделать все действия из пунктов 2)-6) задания 2.
Заполнить последующие строки в таблице 1.
По данным 2-го и последнего столбцов таблицы 1 построить на миллиметровой бумаге график зависимости
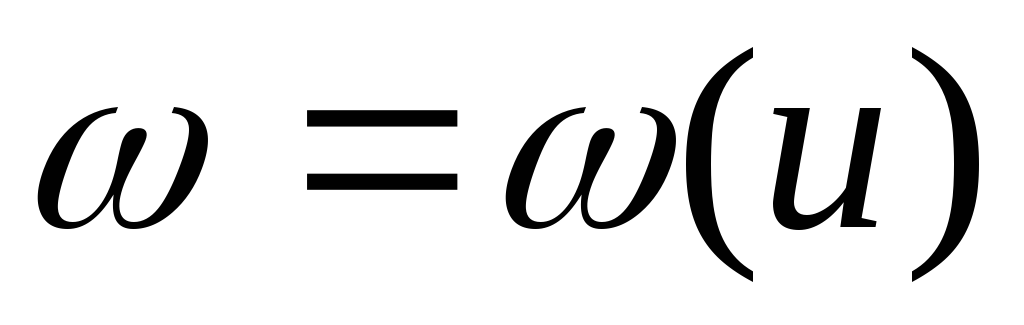 .
Для этого отложить точки, соответствующие
данным таблицы. Соединить эти точки
гладкой кривой. Дополнительно построить
прямую, наиболее близко расположенную
ко всем экспериментальным точкам.
.
Для этого отложить точки, соответствующие
данным таблицы. Соединить эти точки
гладкой кривой. Дополнительно построить
прямую, наиболее близко расположенную
ко всем экспериментальным точкам.Пояснить характер полученной зависимости (обратная пропорциональность, линейная, квадратичная или иная). Сделать вывод о правильности полученных в последнем столбце табл.1 данных и о наличии среди них промахов. Установить возможные причины выявленных промахов.
Имеет ли смысл нахождение среднего значения величины
 по данным в последнем столбце таблицы
1???
по данным в последнем столбце таблицы
1???
Задание 4. Измерение промежутка времени с помощью капельницы.
Ознакомиться с устройством и назначением водной капельницы. Сделать ее рисунок в тетради.
Настроить капельницу на определенную частоту падения капель воды.
С помощью секундомера засечь время
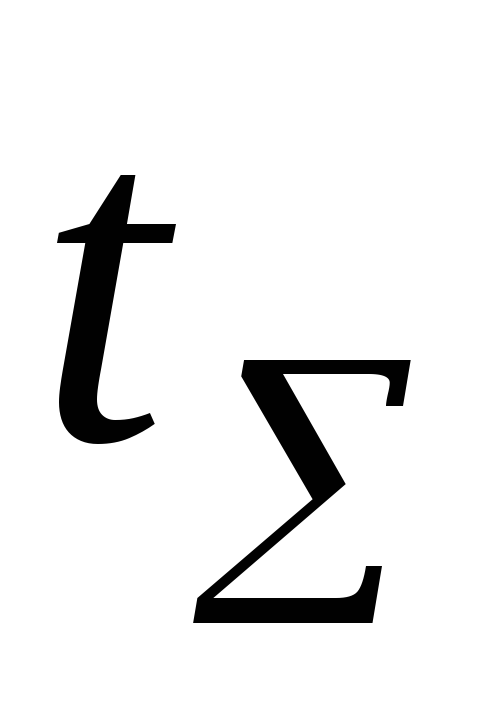 падения 20-30 капель. Провести отсчет
2-3 раза.
падения 20-30 капель. Провести отсчет
2-3 раза.Найти промежуток времени
 между падением двух соседних капель
записать формулу для его расчета.
Пояснить.
между падением двух соседних капель
записать формулу для его расчета.
Пояснить.Настроить метроном в такт с падающими каплями, передвигая подвижный груз Р.
С помощью секундомера определить время
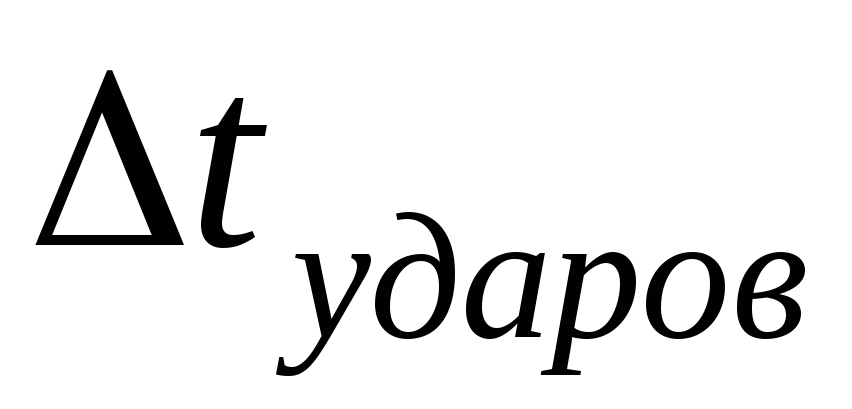 между двумя последовательными громкими
звуковыми «отбиваниями» размахов
метронома.
между двумя последовательными громкими
звуковыми «отбиваниями» размахов
метронома.Записать, чему равен период
 колебания маятника метронома в данном
случае.
колебания маятника метронома в данном
случае.Сравнить полученные значения
 и
и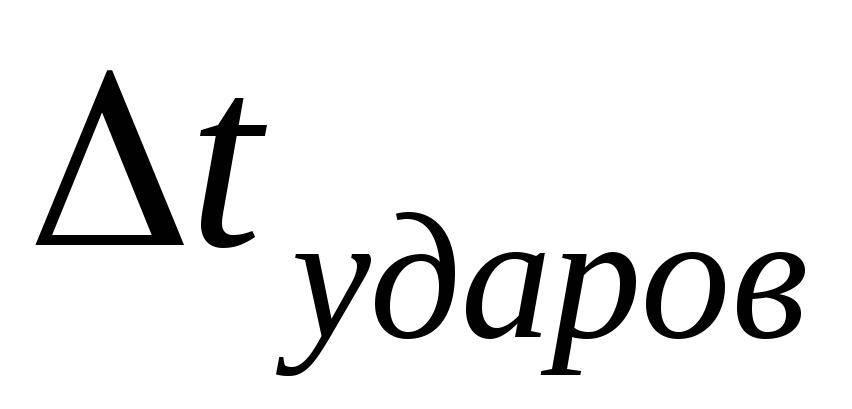 .
Сделать вывод и причинах неточности.
.
Сделать вывод и причинах неточности.
Замечание. Говоря о точности измерений, отличайте ее от точности арифметических вычислений! Погрешность округления результатов вычисления не должна быть значительно меньше общей погрешности соответствующего измерения.
Вопросы к отчету:
Какой промежуток времени в системе единиц СИ принят за 1 с?
Каков общий принцип механических методов измерения времени?
Рассказать о правилах измерения промежутков времени по секундомеру. Какова погрешность таких измерений? Что является источником указанной погрешности?
Что позволяют измерять стробоскопические методы? Что положено в их основу? Какова их точность?
Дать определение частоты и периода вращения. Какое движение при этом рассматривается (движение по окружности, вращательное, то и другое, иное)? Обосновать ответ.
Каким образом можно использовать метроном для измерения промежутка времени?
Лабораторная работа № 1.6.
Измерение скорости звука в воздухе.
Цель работы: познакомиться с основными характеристиками волновых процессов; изучить методы измерения скорости звука в газах; экспериментально определить скорость звука в воздухе методом стоячей волны.
Приборы и принадлежности: металлическая труба с поршнем, звуковой генератор ЗГМ, микрофон, масштабная линейка, кусок мела.
Краткая теория волн.
Любая частица
упругой среды, выведенная из положения
равновесия, под действием упругих сил
стремиться возвратиться в первоначальное
положение и совершает колебания. Если
смещения невелики, упругая сила прямо
пропорциональна смещению, и колебания
будут совершаться по гармоническому
закону:
![]() (1), где
(1), где![]() - величина смещения точки;
- величина смещения точки;![]() и
и![]() - амплитуда и начальная фаза колебаний,
определяемые начальными условиями
(выбором начала отсчета времени можно
добиться выполнение
- амплитуда и начальная фаза колебаний,
определяемые начальными условиями
(выбором начала отсчета времени можно
добиться выполнение![]() ).
).
Колебание одной частицы не остается локализованным – начинают колебаться соседние с ней частицы, затем следующие и т.д.; такая совокупность колеблющихся частиц образует волну. Скорость распространения колебаний (волны), зависящая от природы среды, и амплитуда колебаний определяют величину смещения каждой частицы в заданный момент времени. Распределение величин смещений частиц в волне в зависимости от времени и положения частицы описывается уравнением волны, имеющим вид:
![]() (2), где х
– расстояние частицы от начала координат,
с
– скорость распространения волны, Т
– период колебания,
(2), где х
– расстояние частицы от начала координат,
с
– скорость распространения волны, Т
– период колебания,
![]() - длина волны. Скорость распространения
волн определяется формулой:
- длина волны. Скорость распространения
волн определяется формулой:
![]() (3), где Е
– модуль упругости среды,
(3), где Е
– модуль упругости среды,
![]() - ее плотность.
- ее плотность.
Скорость продольных волн, в которых частицы колеблются вдоль направления распространения волны, определяется модулем упругости (коэффициентом пропорциональности между напряжением и относительной деформацией в законе Гука); скорость волн поперечных, в которых частицы колеблются перпендикулярно к направлению распространения волны, - модулем сдвига.
Появление звука всегда обусловлено колебаниями какого-либо тела. Распространение звука в газах осуществляется продольными волнами.
Уравнение волны (2) соответствует проходящей волне (амплитуда колебаний всех точек волны одинакова, а фаза запаздывает). Если в среде одновременно распространяются 2 волны одинаковой длины, наблюдается сложение этих волн (интерференция). Если направления смещения частиц слагающих волн совпадают, то результирующее смещение равно алгебраической сумме смещений. Тогда результирующее колебание в точке А, отстоящей от первого источника на расстоянии х1, а от второго – на х2, запишется так:
![]() (3), где
(3), где
![]() ,
у01
и у02
– амплитуды 2-х слагающих колебаний
(начальные фазы их предполагаются
совпадающими). Первый множитель в (3) –
результирующая амплитуда колебаний в
заданной точке. Отсюда видно, что при
,
у01
и у02
– амплитуды 2-х слагающих колебаний
(начальные фазы их предполагаются
совпадающими). Первый множитель в (3) –
результирующая амплитуда колебаний в
заданной точке. Отсюда видно, что при
![]() имеем минимум
амплитуды колебаний.
имеем минимум
амплитуды колебаний.
При отражении
проходящей волны от границ раздела 2-х
сред образуется так называемая стоячая
волна
(разные точки колеблются с различными
амплитудами, но с одинаковыми фазами).
Смещение частиц в такой волне определяется
по (3) для суммы прямой и обратной волн.
Надо только иметь в виду, что в случае
отражения от более плотной стенки
амплитуда отраженной волны будет
![]() (т.е. фаза меняется на противоположную
или, иначе говоря, идет потеря
(т.е. фаза меняется на противоположную
или, иначе говоря, идет потеря![]() ).
).
Условие возникновения стоячей волны: наложение двух встречных плоских волн с одинаковыми частотой и амплитудой. Т.е. она возникает, например, при отражении волн от преград.
Распределение смещений (амплитуд) в стоячей волне при отражении от более плотной среды дается уравнением:
![]() (4),
(4),
где
![]() -расстояние
от точки возникновения волны
до места отражения. Переходя от точки
к точке вдоль направления волны, будем
отмечать различные амплитуды колебаний,
определяемые выражением, стоящим перед
косинусом в (8). Отсюда следует наличие
точек (узлов),
для которых эта амплитуда равна нулю:
-расстояние
от точки возникновения волны
до места отражения. Переходя от точки
к точке вдоль направления волны, будем
отмечать различные амплитуды колебаний,
определяемые выражением, стоящим перед
косинусом в (8). Отсюда следует наличие
точек (узлов),
для которых эта амплитуда равна нулю:
![]() (5).
(5).