Файл: ВсяМехЛАБраб2части.doc

Вопросы к отчету.

1. Дайте понятие о моменте силы, моменте импульса, моменте инерции и единицах их измерений.

2. Сравните второй закон Ньютона для вращательного движения со вторым законом для поступательного движения. Какова роль момента инерции во вращательном движении?

3. Как выражается в работе тангенциальное ускорение точек шкива? Какова его связь с угловым ускорением шкива?

4. Какое направление имеет вектор углового ускорения и вектор момента силы?

5. Какие силы действуют на груз P?

6. Изменится ли угловое ускорение, если изменить груз? Какова зависимость между P и  ?

7. Дайте определение механического движения. Что представляет собой вращательное движение? Основные кинематические и динамические параметры вращательного движения.

8. Основная задача механики. Прямая и обратная задачи механики.

9. Физические модели в механике: материальная точка, абсолютно твердое тело, сплошная среда. Границы применимости этих моделей.

10. Центр масс твердого тела. (Центр масс – это единственная точка тела, при приложении к которой внешней силы тело будет двигаться поступательно. При расчетах можно считать, что вся масса тела сосредоточена в этой точке.). Теорема Штейнера (с доказательством).

11. Выведите расчетную формулу (6), пользуясь определениями физических величин и физическими законами.

12. При любом ли расположении масс на крестовине их можно считать точечными?

Лабораторная работа № 2.3.

Изучение законов вращательного движения с помощью махового колеса. (Определение момента инерции махового колеса и силы трения в опоре)

Цель работы: вычисление моментов инерции тел правильной геометрической формы; экспериментальное измерение момента инерции махового колеса методом вращения.

Приборы и принадлежности: маховое колесо, набор грузов, секундомер, штангенциркуль, разновес, измерительная лента.

Краткая теория вопроса.

Вращательное движение осуществляют всегда твердые тела, имеющие конечные размеры (не материальная точка!). Изучая вращательное движение, твердое тело рассматривают или как систему материальных точек или как сплошную среду, заполняющую объем тела. В любом случае по отношению к оси вращения имеется некоторое распределение суммарной массы этого тела. Момент инерции является физической величиной, характеризующей инертность тела к изменению им уг­ловой скорости под действием вращающего момента. Угловая скорость и вращающий момент – также величины, заданные относительно оси вращения.

Опр.1 Моментом инерции материаль­ной точки относительно какой-либо оси называется произведение ее массы на квад­рат расстояния до этой оси: (1)

О пр

(2)

Опр.3 Для тела, понимаемого как сплошная среда с плотностью , момент инерции может быть вычислен путем интегрирования по объему тела:

(3),

где r – расстояние от элемента объема dV до оси, относительно которой вычисляется момент инерции тела.

Момент инерции относительно данной оси, как и масса тела, не зависит от характера движения, а зависит от размеров, формы и плотности тела.

Если момент инерции относительно оси, проходящей через центр массы тела, равен , то момент инерцииотносительно любой другой параллельной оси может быть вычислен на основа­нии теоремы Гюйгенса-Штейнера:(4), гдеd — расстояние между осями.

Основной закон динамики для вращательного движения запи­сывается аналогично второму закону Ньютона с эквивалентной заменой величин, описывающих поступательное движение, на величины, характеризующие вращательное движение: (5), где — сумма моментов сил, действующих на тело,— угловаяскорость вращения. Если =0, то или.

Величина называется моментом количества (вращательного) движения. Та­ким образом, если на вращающееся тело не действует вращающий момент, оно будет вращаться неопределенно долго, сохраняя по­стоянным имеющийся у него момент количества движения.

Для замкнутой системы имеет место закон сохранения момента количества движения.

Итак, в случае вращательного движения момент инер­ции играет такую же роль, как масса при поступательном движе­нии, а угловая скорость — роль линейной.

Математическая форма записи основных закономерностей для поступательного и вращательного движения остается неизменной, что видно из следующей таблицы.

Описание прибора и метода

В состав прибор входит маховое колесо, вали шкив, отсчетная линейка (рис. 2).Колесо жестко связано со шкивом и вместе они могут вращаться на валу. На поверхность шкива наматывается нить, к концу которой прикреплен груз массой т.

П

рис.2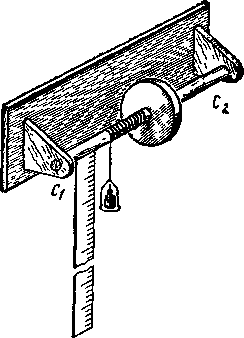

(6),

где А’_тр.1=А∙N₁ — работа по преодолению силы трения за N₁ оборотов колеса (А’_тр.1 >0), A - работа по преодолению трения за 1 оборот. Работа силы трения всегда зависит от пройденного расстояния.

- кинетическая энергия груза в конце пути,

- кинетическая энергия махового колеса в тот же момент времени.

N₁ – число оборотов за время падения груза.

Уравнение (6) связывает начальное и конечное состояния системы «маховое колесо-груз»: “груз на высоте h, груз и колесо покоятся” и “груз на нулевом уровне, имеет скорость, и колесо вращается”.

Силу трения можно вычислить, исходя из следующих соображе­ний. В момент достижения грузом пола, нить к которой он привязан, спадает со шкива, а маховое колесо продолжает вращаться до тех пор пока его кинетическая энергия не будет израсходована на работу по преодолению трения. Вращаясь после падения груза, маховое колесо совершает до полной остановки N₂ оборотов за время t. Убыль кинетической энергии равна работе по преодолению силы трения: