Файл: Faustova.docx

Задачи изучения темы

1. Формирование у младших школьников чётких представлений и понятий о предусмотренных программой геометрических фигурах (точка, прямая линия, кривая линия, отрезок прямой, ломаная линия, угол, многоугольник, круг).

2. Развитие пространственных представлений, умений наблюдать, сравнивать, абстрагировать и обобщать.

3. Формирование измерительных навыков, практических умений построения предусмотренных программой геометрических фигур с помощью чертёжных инструментов.

2.2.Основные положения методики изучения геометрического материала

В изучении геометрического материала, как видим, можно выделить две линии: а) геометрия формы; б) геометрия измерения.

Главная цель – накопление конкретных представлений (наглядная геометрия), усвоение соответствующего термина ( определённый уровень обобщения – эмпирический или понятийный – прямоугольник и квадрат).

Основной метод изучения – лабораторно – практические работы

(изготовление моделей, черчение, измерение). Необходимо варьировать несущественные признаки рассматриваемых геометрических объектов. Следовательно, должно быть достаточное разнообразие наглядного материала как демонстрационного, так и индивидуального. Необходимо, чтобы как у учителя, так и у каждого ученика были чертёжные инструменты ( линейка, треугольник, циркуль).

При формировании представлений о фигурах большое значение придается проведению практических упражнений, связанных не только с построением, вычерчиванием геометрических фигур, но и с преобразованием одних фигур в другие, с рассмотрением некоторых свойств изучаемых фигур (например, свойства противоположных сторон прямоугольника, диагоналей прямоугольника и квадрата), упражнений, направленных на развитие геометрической зоркости (умения узнавать геометрические фигуры на сложном чертеже, составлять заданные геометрические фигуры из частей и др.).

Работа над геометрическим материалом по возможности увязывается с изучением арифметических вопросов. Так, с самого начала геометрические фигуры и их элементы используются в качестве объектов счета предметов. После ознакомления с измерением длины отрезка рассматриваются задачи на нахождение суммы и разности двух отрезков, длины ломаной, периметра многоугольника и в том числе прямоугольника (квадрата), а в дальнейшем и площади прямоугольника (квадрата). Нахождение площади прямоугольника (квадрата) связывается с изучением умножения, задача нахождения стороны прямоугольника (квадрата) по его площади — с изучением деления.

Различные геометрические фигуры (отрезки, многоугольники, круг) используются и в качестве наглядной основы при формировании представлений о долях величины, а также при решении разного рода текстовых задач. В последнем случае речь идет об использовании схематических чертежей, отражающих описанные в задаче связи между данными и искомым.

Изучение геометрического материала, кроме того, бесспорно оказывает большое влияние на развитие как конкретного, так и абстрактного мышления у детей.

2.3. Методика изучения основных геометрических фигур Точка, прямая и кривая линии, отрезок прямой

У учащихся I—IV классов надо сформировать четкие представления точки, прямой и кривой линий, отрезка прямой. Задача учителя - научить вычленять, называть и правильно показывать эти фигуры, изображать их на бумаге и на доске, начиная с III класса - обозначать с помощью букв. Дети должны научиться измерять и чертить отрезки заданной длины.

С точкой учащиеся знакомятся с первых шагов обучения в I классе. Готовясь к письму цифр, дети по образцу учителя выполняют такие задними: поставьте точку в середине клеточки (в левом нижнем углу клетки, в середине одной из сторон клетки и т. п.); соедините gоставленные точки отрезками по образцу. Образ точки может ассоциироваться у ребёнка с размером отверстия от прокола листа бумаги толстой иглой.

После знакомства с прямой линией дети учатся ставить точки на прямой, проводить прямые линии через 1, 2 заданные точки.

После знакомства с отрезком прямой аналогичные задания выполняются с точкой и отрезком, при этом дети убеждаются, что точка, лежащая между концами отрезка, делит его на два отрезка.

Когда происходит знакомство с элементами многоугольника, учащиеся узнают о том, что вершины многоугольников - это точки. Например, учитель предлагает детям поставить 3 точки так, как показано на доске (точки не лежат на одной прямой), соединить их отрезками и сказать, какая фигура получилась; затем сосчитать, сколько у нее вершин.

В III классе учащиеся знакомятся с обозначением точек латинскими буквами. Учитель поясняет, что для различения точек на чертеже принято обозначать их заглавными латинскими буквами, например: О, К, М, С, A, Е и т. д., которые пишутся около точки (показывается образец на доске). Дети упражняются в обозначении точек буквами и чтении обозначенных буквами точек. С этого времени наряду с устными упражнениями можно включать и письменные, что гораздо эффективнее, так как заставляет работать каждого ребенка. Например, по чертежу, данному на доске, предлагают выписать в первую строчку те точки, которые лежат внутри круга (четырехугольника), во вторую строчку - точки, которые лежат вне круга (четырехугольника), в третью строчку - точки, которые лежат на границе круга (четырехугольника).

Формирование у первоклассников представления о прямой линии происходит в процессе выполнения ими разнообразных практических заданий. При этом прямую линию сопоставляют с кривой. Например, натягивают нить (шнур, шпагат), затем ослабляют нить так, чтобы она провисала; рассматривают рисунки, на которых изображена, положим, прямая дорога и извилистая тропинка, разрезают лист бумаги по линии, полученной перегибанием листа, и т. п. Каждый раз выясняют, какая получилась линия - прямая или кривая.

Дети должны научиться узнавать прямую линию, начерченную в любом положении на плоскости, отличать ее от кривой, уметь проводить прямые, используя линейку. С целью формирования этих умений учащиеся чертят в тетрадях прямые и кривые линии, находят и показывают их на окружающих предметах, а также среди линий, начерченных на доске.

В процессе выполнения заданий в проведении линий через точки дети обобщают свои наблюдения: через одну точку можно провести сколько угодно прямых или кривых линий; через две точки можно провести только одну прямую, а кривых сколько угодно.

С отрезком прямой учащиеся знакомятся также практически: отмечают на прямой две точки, и учитель поясняет, что эту часть прямой от одной точки до другой называют отрезком прямой, или кратко - отрезком, а точки - концами отрезка. Дети ставят точки на других прямых, начерченных на доске, и показывают полученные отрезки и концы отрезков. Затем учитель показывает, как изображается на чертеже отрезок (концы отрезка отмечает точками или штрихами), сравнивает с изображением прямой. Учащиеся показывают на чертежах и сами чертят прямые и отрезки прямых и постепенно осознают, что отрезок ограничен, а прямая не ограничена, мы изображаем на бумаге только часть прямой. Закреплению понятия об отрезке способствует выполнение таких заданий: показать отрезки прямой на окружающих предметах; соединить отрезком две точки; провести отрезок через три точки, лежащие на одной прямой; показать все получившиеся при этом отрезки. До измерения отрезков дети учатся сравнивать их наложением, чтобы установить, какой из них короче (длиннее) или отрезки одинаковой длины.

В дальнейшем после знакомства с сантиметром, дециметром, метром и т.д. учащиеся выполняют большое количество заданий в измерении и черчении отрезков, решают задачи с отрезками (на увеличение и уменьшение на несколько единиц и в несколько раз, на разностное и кратное сравнение). Постепенно учащиеся убеждаются, что равные отрезки содержат одинаковое число выбранных единиц длины, а неравные - неодинаковое число: в том отрезке содержится больше единиц, который длиннее. Таким образом, становится возможным судить о равенстве и неравенстве отрезков на основе сравнения их длин.

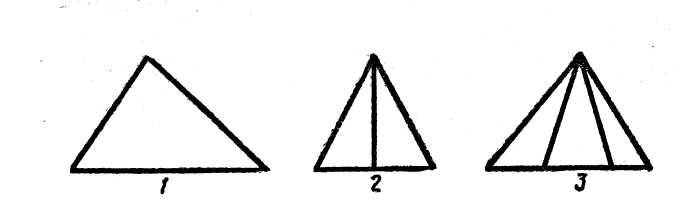
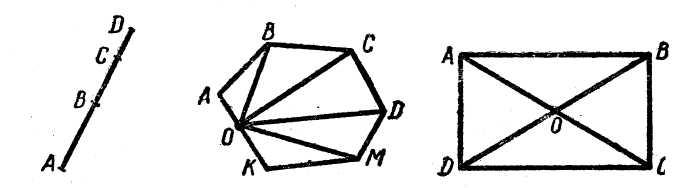
Выделяя элементы многоугольников, учащиеся устанавливают, что стороны многоугольников - отрезки. Задания на выделение отрезков необходимо усложнять постепенно, чтобы они были посильны учащимся. Так, чтобы дети смогли увидеть и показать все отрезки на таких чертежах, надо научить их выполнять более легкие задания - называть и показывать отрезки на чертежах, подобных первому и второму.

Когда учащиеся ознакомятся в Ш классе с обозначением отрезков буквами, даются письменные задания, которые закрепляют умения выделять отрезки, являющиеся частями других отрезков, а также отрезки, составленные из других отрезков. Например, предлагают записать все отрезки, которые имеются на чертеже, записать отрезки с началом в точке О, измерить с помощью линейки и выписать равные отрезки.

Постепенно учащиеся осознают, что отрезок может быть общей стороной нескольких многоугольников и, опираясь на это в III - IV классах выполняют задания на построение отрезков внутри многоугольников, так, чтобы при этом образовывались новые фигуры; например, провести внутри пятиугольника один отрезок так, чтобы при разрезании получились треугольник и четырехугольник или два четырехугольника, или треугольник и шестиугольник. Учащиеся выполняют задание в тетрадях, а затем выявляются и показываются на доске различные решения каждой задачи. Такие упражнения расширяют у детей воображение и пространственные представления, а также закрепляют геометрические понятия.