Файл: UP_po_zadacham.doc

Рассмотрим полное рассуждение ученика при решении ранее рассмотренной задачи на нахождение суммы.

Мне известно, что мама купила 5 яблок и 4 груши.

Надо узнать, сколько всего фруктов купила мама.

Рисую и объясняю. Обозначу каждый фрукт точкой. Рисую 5 точек, обвожу замкнутой линией, столько яблок купила мама. Рисую 4 точки, обвожу замкнутой линией, столько груш купила мама. Обвожу замкнутой линией все точки. Столько всего фруктов купила мама. Это мне неизвестно, обозначу вопросительным знаком.

На доске постепенно появляется «картинка с точками»:

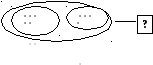
Подумаю, надо объединять или удалять...

Чтобы узнать, сколько всего фруктов купила мама, я объединю все яблоки и груши.

Подумаю, надо прибавлять или вычитать...

Я объединял фрукты, буду прибавлять.

Запишу решение задачи:

5 + 4 = 9 (фр.) - столько всего фруктов купила мама.

Ответ: 9 фруктов.

Проверку правильности решения задачи в этот период дети самостоятельно не выполняют: она осуществляется с помощью учителя.

Письменные пояснения к выполненному действию также не выполняются.

Таким образом, памятка по решению задачи будет иметь вид:

Рассуждаю так:

1. Мне известно...

2. Надо узнать...

3. Рисую и объясняю...

4. Подумаю, надо объединять или удалять...

5. Подумаю, надо прибавлять или вычитать...

6. Выполняю решение…

7. Отвечаю на вопрос задачи…

7.2. На основе анализа деятельности ученика по решению задачи выделяем, чему должен научиться ребёнок на этапе подготовки к введению задач на нахождение суммы и остатка, и на основе этого моделируем подготовительный этап.

На подготовительном этапе к введению задач на нахождение суммы и остатка ребёнок должен научиться:

а) Выделять из множества его подмножество с данной численностью по какому-либо одному или нескольким признакам и изображать это подмножество в виде «картинки с точками».

б) Выполнять практически операцию объединения множеств с заданной численностью, изображать операцию с помощью «картинки с точками» и находить численность получившегося множества с помощью присчитывания (отсчитывания).

в) Устанавливать связь между операцией объединения множеств и арифметическим действием сложения (между операцией удаления из множества его правильной части и действием вычитания), выполняя его в неявном виде: «5 да ещё 4, стало 9»(5 без 2, стало 3).

Для решения поставленных задач детям предлагаются практические задания на выделение из множества подмножества с данной численностью, изображение подмножества в виде «картинки с точками», практическое выполнение операции объединения множеств, изображение её в виде «картинки с точками», нахождение численности получившегося множества.

Приведём примеры таких заданий.

1. Учитель предлагает детям положить перед собой на парте 4 круга(3 красных квадрата, 2 больших синих треугольника и т.д.).

2. На наборное полотно ставятся 5 красных кругов и предлагается ученикам нарисовать в тетради столько же кругов, сколько на наборном полотне. Затем учитель убирает круги с наборного полотна и спрашивает:

- Сколько кругов было на наборном полотне? ( 5.)

- Как вы можете это доказать? (У нас в тетради нарисовано кругов столько же, сколько было на наборном полотне.)

После этого учитель ставит на наборное полотно 6 карточек с нарисованными на них машинами.

- Нарисуйте в тетради столько же машин, сколько я поставила на наборное полотно.

В процессе беседы выясняется, что это трудно и долго.

- Как вы думаете, после того, как вы нарисуете машины в тетради, а я уберу с наборного полотна эти картинки, о чём я у вас спрошу? (Сколько было машин на наборном полотне?)

- Как вы считаете, обязательно ли рисовать именно машины, чтобы ответить на этот вопрос? (Нет.)

- Какой выход можно найти из этой ситуации? (Можно вместо машин нарисовать круги, квадраты).

- Можно каждую машину обозначить точкой?

- Сколько точек нарисуете? (Выполняют в тетради, учитель на доске.)

- Покажем, что все машины изобразили, обведём все точки замкнутой линией (Учитель собирает карточки с машинами в одну пачку и ставит на наборное полотно.).

- Сколько же было машин на наборном полотне? (6.)

- Как вы можете это доказать?

После выполнения 2-3 таких заданий, детям предлагается «картинка с точками», говорится про что она нарисована (например, про розы) и спрашивается, о чём по ней можно рассказать (В вазе 3 розы.).

Поставьте на наборное полотно слева 3 красных круга, возьмите 2 синих круга и поставьте их на наборное полотно справа (Дети выполняют и показывают наборные полотна учителю.). Придвиньте синие круги к красным, объедините синие и красные круги. Скажите не считая, сколько всего кругов на наборном полотне? (3 да ещё 2.) Сколько всего кругов на наборном полотне? (Присчитывают вслух синие круги к красным, говорят: 5.)

- Нарисуем «картинку с точками» сначала про красные круги. Как обозначите каждый круг? Сколько нарисуете точек? Рисуйте и вслух объясняйте, что делаете. (Учитель выполняет на доске, дети вместе с ним рисуют и проговаривают: «Рисую 3 точки, обвожу их замкнутой линией. Столько положили красных кругов». Нарисуем рядом «картинку с точками» про синие круги. Сколько точек будете рисовать? (Выполняется аналогично.) Нам нужно узнать, сколько всего кругов на наборном полотне? Что для этого нужно с кругами сделать? (Показывают вместе с учителем жестом и говорят: «Объединить красные и синие круги».) На «картинке с точками» это изображают так: обводят замкнутой линией все точки, чтобы показать, что это все круги. Как получили 5? (3 да ещё 2, стало 5.)

«Картинка с точками» имеет в данном примере следующий вид:

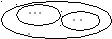
2) Возьмите 4 треугольника, поставьте их на наборное полотно, отодвиньте, удалите 1 треугольник. Скажите не считая, сколько треугольников осталось? (4 без 1.) Сколько треугольников осталось? (Один ученик выполняет на наборном полотне или на магнитной доске.) Далее выполняется «картинка с точками». Работа организуется аналогично предыдущему заданию. Рассуждение ученика, выполняемое вместе с учителем, звучит следующим образом: «Обозначу каждый треугольник точкой. Рисую 4 точки, обвожу замкнутой линией. Столько было всего треугольников. Обвожу замкнутой линией одну точку, столько треугольников отодвинули. Обвожу замкнутой линией остальные точки. Столько треугольников осталось. Покажите жестом и скажите, что нужно сделать с одним треугольником, чтобы узнать, сколько треугольников осталось? (Удалить.) На «картинке с точками» это изображается так: перечёркивают крестом те точки, которые удаляют. Сколько треугольников осталось? Как получили число 3? (4 без 1, стало 3.)

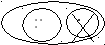
3) На доске «картинка с точками»:

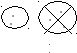
- Это «картинка» про карандаши. О чём можно по ней рассказать? (У мальчика было 5 карандашей. 3 карандаша он отдал.) Что надо узнать? (Надо узнать, сколько карандашей осталось.) Спрашивается, что показывает каждая из «картинок» - частей всей «картинки». Затем предлагается показать жестом и сказать, как можно узнать, сколько карандашей осталось у мальчика. (Из 5 карандашей удалить 3 карандаша.) Скажите не считая, сколько осталось карандашей у мальчика? (5 без 3.) Сколько осталось карандашей у мальчика? (2.)

На ступени ознакомления с задачами на нахождение суммы и остатка (они вводятся одновременно) осуществляется, во-первых, подготовительная работа к овладению общим умением решать задачи (знакомство с задачей (контекстуально), структурой задачи (дети подводятся к пониманию того, что каждая задача состоит из условия и вопроса; условие отражает то, что известно в задаче, вопрос - то, что надо узнать); процессом её решения (усваивают какие операции, в каком порядке выполняются при решении задач рассматриваемого вида); во-вторых, усваивают теоретическую основу выбора арифметического действия в задачах этого вида.

Выделим виды заданий, предлагаемых детям для решения выше указанных задач.

Задания для осознания детьми структуры задачи

1) Выполнение схемы к данной задаче, преобразование задачи по схеме задачи из стандартной структуры в нестандартную и обратно.

2) Составление задачи на основе использования предметной наглядности, «схемы задачи».

3) Составление задачи по «картинке с точками», по данному условию, вопросу.

Рассмотрим фрагмент урока, на котором дети впервые встречаются с терминами «задача» (контекстуально), «условие задачи», «вопрос задачи».

- Внимательно наблюдайте за тем, что я делаю. У мальчика было 3 красных яблока (показывает картинки с яблоками и ставит их на наборное полотно) и 2 зелёных яблока (поступает аналогично). Скажите, что мы знаем о яблоках? Что мы можем узнать про яблоки? (Сколько всего яблок было у мальчика?) Давайте повторим, что мы знаем о яблоках? Что надо узнать? Мы составили с вами задачу. Повторим всю задачу.

- Нарисуем к задаче, которую мы с вами составили, схему. Повторите, что мы знаем. Это условие задачи, в условии говорится о том, что известно в задаче. Изобразим его одной чертой (рисуют: дети в тетрадях, учитель на доске). Что надо узнать в задаче? Это вопрос задачи, в вопросе говорится о том, что надо узнать. Изобразим его двумя чертами (выполняют в тетрадях).

Это схема задачи: . В задаче всегда есть условие и вопрос. Затем под руководством учителя осуществляется решение задачи. Работа над другими задачами на нахождение суммы и остатка строится аналогично (сначала выполняется схема задачи, затем решение). В конце урока подводится итог: что нового узнали на уроке?

Задания для усвоения детьми теоретической основы выбора арифметического действия

Усвоению детьми теоретической основы выбора арифметического действия способствовало выполнение на основе использования модели объекта действия заданий, позволяющих овладеть умением устанавливать связи между данными и искомым в конкретной ситуации, описанной в задаче, и между операцией над множествами и соответствующим арифметическим действием:

1) Выполнение иллюстраций в виде «картинки с точками» в процессе решения задачи.

2) Составление задачи по иллюстрации.

3) Выполнение «картинки с точками» по математическому выражению, составление задачи и её решение.

При выполнении этих заданий дети в процессе практических действий осуществляют переход не только от конкретной ситуации, описанной в задаче к арифметическому действию, но и обратно: от арифметического действия к операции над множествами, а затем к конкретной ситуации, что позволяет им видеть общее в частном и частное в общем.

Приведём фрагмент урока, на котором при выполнении задания дети самостоятельно составляют задачу на основе использования модели в виде «картинки с точками» и записывают её решение.

На доске учителем выполняется иллюстрация в виде «картинки с точками»:

Сначала детям предлагается внимательно посмотреть на «картинку с точками», подумать, что нужно сделать с предметами, чтобы ответить на вопрос задачи, затем каждому самостоятельно составить задачу и записать на наборном полотне её решение. Один ученик выполняет задание на отвороте доски. Затем несколько детей воспроизводят вслух составленную ими задачу, одна из них решается. После её решения ученикам ставится вопрос: «Почему задачи разные, а решались одинаково?», т.е. дети подводятся к обобщению связи операции над множествами с соответствующим арифметическим действием.

Задания для усвоения системы операций, составляющих процесс решения простой арифметической задачи

1) Усвоение содержания и порядка следования операций в процессе выполнения задания «Закончи предложение» и инсценирования, работе по «памятке».

2) Усвоение содержания операций в процессе их выполнения под руководством учителя в процессе решения простых арифметических задач. Для усвоения системы операций, составляющих процесс решения простой арифметической задачи, т.е. структуры деятельности, работу можно организовать следующим образом. Сначала дети усваивают содержание каждой операции и с помощью учителя выполняют их в определённом порядке. В качестве примера приведём фрагмент одного из уроков.