Файл: UP_po_zadacham.doc

Задача на нахождение неизвестного уменьшаемого

Задача. После того как девочка отправила 6 открыток, у неё осталось 4 открытки. Сколько открыток было у девочки?

Мне известно, что девочка отправила 6 открыток, и у неё осталось 4 открытки.

Надо узнать, сколько открыток было у девочки.

Рисую и объясняю. Обозначу каждую открытку точкой. Рисую 6 точек, обвожу замкнутой линией. Столько открыток девочка отправила.

Рисую 4 точки, обвожу их линией. Столько открыток осталось. Обвожу линией все точки, столько открыток было у девочки. Это мне неизвестно, обозначу вопросительным знаком.

Подумаю, нужно объединять или удалять. Чтобы узнать, сколько открыток было у девочки, надо объединить открытки, которые девочка отправила и те, которые у неё остались.

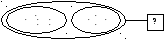
Подумаю, надо прибавлять или вычитать. Я объединял открытки, буду прибавлять.

Выполняю решение. К 6 прибавить 4, получится 10.

Отвечаю на вопрос задачи. У девочки было 10 открыток.

Задача на нахождение неизвестного вычитаемого

Задача. Девочке нужно вымыть 8 тарелок. После того, как она вымыла несколько тарелок, ей осталось вымыть 3 тарелки. Сколько тарелок вымыла девочка?

Мне известно, что девочке нужно вымыть 8 тарелок и что 3 тарелки она уже вымыла.

Надо узнать, сколько тарелок девочка вымыла. Рисую и объясняю.

Обозначу каждую тарелку точкой. Рисую 8 точек, обвожу замкнутой линией. Столько было тарелок. Обвожу линией 3 точки, столько тарелок осталось вымыть. Обвожу линией остальные точки, столько тарелок вымыла девочка. Это мне неизвестно, обозначу вопросительным знаком.

Подумаю, нужно объединять или удалять. Чтобы узнать, сколько тарелок вымыла девочка, надо из всех тарелок удалить те тарелки, которые остались.

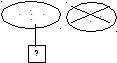
Подумаю, надо прибавлять или вычитать. Я удалял тарелки, буду вычитать. Выполняю решение. Из 8 вычесть 3, получится 5.

Отвечаю на вопрос задачи. Девочка вымыла 5 тарелок.

Как видим, если задачи на нахождение неизвестных компонентов арифметических действий сложения и вычитания ввести на ступени закрепления умения решать арифметические задачи на нахождение суммы и остатка, то специальной подготовительной работы не потребуется, т.к. содержательные знания (о задаче, её структуре, обосновывающие выбор арифметического действия) и операционные знания сформированы у детей в процессе решения задач на нахождение суммы и остатка.

7.4. Методика формирования умения решать простые арифметические задачи на нахождения произведения, деление по содержанию и на равные части

Задачи на нахождение произведения, деление по содержанию и на равные части вводятся во 2 классе при изучении конкретного смысла арифметических действий умножения и деления. Собственно говоря, в процессе их решения и усваивается конкретный смысл обоих арифметических действий. Сначала вводятся задачи на нахождение произведения (теоретическая основа выбора арифметического действия - конкретный смысл действия умножения), затем задачи на деление по содержанию, вслед за ними деление на равные части (теоретическая основа выбора арифметического действия- конкретный смысл действия деления).

Задачи на нахождение произведения

Задача. На 3 тарелки положили по 5 яблок на каждую. Сколько всего яблок положили?

Полное рассуждение ученика. Мне известно, что на 3 тарелки положили по 5 яблок на каждую.

Надо узнать, сколько всего яблок положили.

Рисую и объясняю. Обозначу каждое яблоко точкой, рисую 5 точек, обвожу замкнутой линией. Столько яблок на одной тарелке. Рисую ещё 5 точек, обвожу линией. Столько яблок на второй тарелке и т.д. Обвожу линией все точки, столько яблок на 3 тарелках. Это мне неизвестно, обозначу вопросительным знаком.

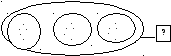
-Чтобы узнать, сколько всего яблок на тарелках, надо объединить поровну по 5 яблок.

а) Объединила поровну по 5, буду прибавлять (подготовительный этап).

Запишу решение: 5+5+5=15(яб.)

б) По 5 взяли 3 раза, буду умножать.

Запишу решение: 5•3=15 (яб.)

Отвечаю на вопрос задачи. Всего на тарелках 15 яблок.

2) Чтобы узнать, сколько всего яблок, надо объединить поровну. Буду умножать.

Запишу решение: 5•3=15 (яб.)

Отвечаю на вопрос задачи. Всего на тарелках 15 яблок.

Анализ полного рассуждения ученика показывает, что к моменту введения задач на нахождение произведения он должен:

1) Практически выполнять операцию объединения равночисленных непересекающихся множеств с заданной численностью и заданным числом множеств, изображать операцию объединения равночисленных непересекающихся множеств в виде «картинки с точками».

2) Устанавливать связь между операцией объединения этих множеств с арифметическим действия сложения и находить численность получившегося множества путём сложения.

3) Владеть операционными знаниями по решению задачи.

Из этого вытекают задачи подготовительной работы к решению задач этого вида, которая начинается во 2 кл. классе при изучении сложения и вычитания в процессе выполнения заданий вида:

а) Положите по 2 круга 4 раза. Как вы думаете, чтобы узнать, сколько всего кругов, что нужно с ними сделать, покажите жестом и скажите (Объединить все круги). Каким действием будем находить, сколько всего кругов? Почему? (Мы объединяли круги, значит надо прибавлять). Запишите решение. Дети записывают: 2+2+2+2=8. Далее устанавливают, что слагаемые этой суммы одинаковые и что их 4.

б) Учитель читает задачу: «Было 4 коробки цветных карандашей по 6 штук в каждой. Сколько всего карандашей было?». После прочтения задачи учитель спрашивает детей, как они понимают выражение «в каждой» (в первой коробке 6 карандашей, во второй - тоже 6, в третьей 6 карандашей и в четвёртой 6 карандашей). Затем он предлагает детям вместе решить эту задачу, рассуждая вслух по памятке и выполняя «картинку с точками».

Мне известно, что было 4 коробки по 6 карандашей в каждой.

Надо узнать, сколько всего карандашей.

Рисую и объясняю. Обозначу каждый карандаш точкой. Рисую 6 точек, обвожу линией. Столько карандашей в одной коробке. Рисую ещё 6 точек, обвожу линией. Столько карандашей во второй коробке и т.д.

Обвожу линией все точки, столько всего карандашей. Это мне неизвестно, обозначу вопросительным знаком.

Чтобы узнать, сколько всего карандашей, надо их объединить.

Учитель обращает внимание детей на то, что объединяют равные количества карандашей и что в этом случае будем говорить «объединяю поровну».

Объединял поровну карандаши, буду прибавлять.

Запишу решение: 6+6+6+6=24 (кар.)

Отвечаю на вопрос задачи. Всего 24 карандаша.

На этом же этапе целесообразно предлагать детям творческие задания: составление задач по «картинке с точками», по решению; выполнение «картинки с точками» по заданному решению и др. Работа в этом случае организуется аналогично работе с задачами на нахождение суммы и остатка.

Таким образом, на подготовительной ступени дети усваивают первую ступень в конкретном смысле умножения: от операции над множествами к сложению одинаковых слагаемых.

Во 2 же классе происходит ознакомление с задачами на нахождение произведения. В процессе решения задач, аналогичных предложенной ранее, детям раскрывается содержание второй ступени конкретного смысла умножения: от сложения одинаковых слагаемых к арифметическому действию умножения. Так, если при решении задачи с полным рассуждением и выполнением «картинки с точками» дети получают решение 6+6+6+6=24, то учитель обращает внимание на то, что слагаемые одинаковые и можно сказать так: по 6 взяли 4 раза. Математики договорились в таком случае, когда слагаемые одинаковые, записывать это действие короче: 6•4=24, где число 4 показывает, сколько раз число 6 берётся слагаемым. Читают такую запись следующим образом: по 6 взять 4 раза, получится 24; 6 умножить на 4, получится 24.

Как считает М.А. Бантова, двойной записью (6+6+6+6=24 и 6•4=24)надо пользоваться дольше, т.к. в этом случае дети лучше усваивают смысл каждого компонента умножения в записи решения.

На этапе закрепления умения решать задачи на нахождение произведения учащиеся должны постепенно перейти от выполнения сложения и умножения к выполнению сразу действия умножения. Сначала им предлагается про себя объяснить решение сложением, а вслух назвать или записать решение умножением. Постепенно дети научатся выбирать сразу действие умножения, минуя сложение. На этапе закрепления выполняются разнообразные задания, которые позволяют закрепить знание конкретного смысла умножения и формировать умение решать задачи на нахождение произведения: решение аналогичных задач сначала с полным рассуждением, а затем с кратким; составление задач по решению (например, 5•3=15), по «картинке с точками», преобразование задач из стандартной структуры в нестандартную и обратно и др. (см. работу над задачами на нахождение суммы и остатка на этапе закрепления).