ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.08.2024
Просмотров: 1754
Скачиваний: 0
СОДЕРЖАНИЕ
1.4. Декартово произведение множеств
1.5.1. Определение бинарного отношения
1.5.2. Способы задания бинарного отношения
1.5.3. Свойства бинарных отношений
1.5.4. Отношения эквивалентности
1.7. Контрольные вопросы и упражнения
2.1.1. Логические высказывания
2.1.2. Основные логические операции
2.2.1. Булевы функции и операции
2.2.2. Совершенные дизъюнктивная и конъюнктивная нормальные формы
2.3. Полные системы логических функций
Класс функций, сохраняющих ноль
Класс функций, сохраняющих единицу
Класс самодвойственных функций
2.4.3. Минимизация днф методом Квайна
2.6. Контрольные вопросы и упражнения
3.1.2. Ориентированные и неориентированные графы
3.1.4. Частичные графы и подграфы
3.1.6. Изоморфизм. Плоские графы
3.2. Отношения на множествах и графы
3.3. Матрицы смежности и инциденций графа
3.5.1. Степени неориентированных графов
3.5.2. Степени ориентированных графов
3.6.1. Характеристики расстояний в графах
3.6.2. Характеристические числа графов
3.7.2 . Базисные циклы и разрезающие множества
Свойства базисных циклов и разрежающих множеств
3.7.3. Цикломатическая матрица и матрица разрезов
Составление цикломатической матрицы
3.8. Задача определения путей в графах
3.8.1. Определение путей в графе
3.8.2. Алгоритм определения кратчайших путей
2. Отношение Rна множествеXназываетсясимметричным, если из условия (х, у)Rследует (у, х)R. ОтношениеRна множествеXназываетсянесимметричным, если для любых х, уXиз условия (х,y)Rследует (у, х)R.
3. Отношение Rна множествеXназываетсятранзитивным, если для любых х, у,zRиз одновременного выполнения условий (x,y)Rи (у,z)Rследует (х,z)R.
Пример. Рассмотрим следующие отношения на множестве X = {1,2,3,4,5,6,7}:
G = {(x, y) | х, у Х; х > у};
L = {(х, у) | х, у Х; х у};
M = {(x, y) | х, у X; (х - у) делится на 3};
К = {(х, y) | х, у Х; х2 + у2 20}.
Исследуем, какими свойствами они обладают.
Среди приведенных в примере отношений рефлексивными являются отношениеL(т. к. хх справедливо при всех хX) и отношение М (т. к. х - х = 0 делится на 3, поэтому пара (х, х) принадлежит отношению М при всех х X).
Симметричными являются отношения М (если х - у делится на 3, то и у - х делится на 3) и К (если х2 + у2 20, то и у2 + х2 20).
Транзитивными являются отношения G, L, М.
1.5.4. Отношения эквивалентности
Бинарные отношения делятся на типы в зависимости от свойств, которыми они обладают.
Отношение Rна множествеXназываетсяотношением эквивалентности, если оно обладает свойствами рефлексивности, симметричности и транзитивности.
Важной особенностью отношений эквивалентности является то, то они разбивают все множество Х на непересекающиеся подмножества – классы эквивалентности.
Классом эквивалентности, порожденным элементом хX, называется подмножество [х] множестваX, для элементов которого выполняется условие (х, у)R,yX.
Таким образом, класс эквивалентности:
[х] = {у | y X; (x, y) R}.
Классы эквивалентности образуют систему непустых непересекающихся подмножеств множества X, в объединении дающую все множество X – т. е. образуют разбиение множества Р(Х).
Обозначим отношение эквивалентности символом , тогда класс эквивалентности записывается в виде:
[х] = {у | y X; х у}.
Из рассмотренных в примере отношений только отношение М является отношением эквивалентности.
Отношение М разбивает множество X = {1,2,3,4,5,6,7} на три класса эквивалентности:
[1] = {1,4,7}, [2] = {2,5}, [3] = {3,6}. Классы, порожденные элементами 4, 5, 6 и 7 совпадают с этими классами:
[4] = [1], [5] = [2], [6] = [3], [7] = [1]. 1.6. Отображения множеств
Пусть XиY– два непустых множества. ЗаконG, согласно которому любому элементу хXставится в соответствие элемент уY, называетсяоднозначным отображением XвY. Отображение является обобщением понятия функции, определенной наXи принимающей значения наY.
Используются следующие эквивалентные записи:
G:XY
или
у = G(x); где х X , у Y.
В случае однозначного отображения элемент у называется образом элемента х, а х – прообразом у.
Возможна ситуация, когда каждому х X отображение G ставит в соответствие некоторое подмножество G(x) Y. Тогда образом элемента х будет подмножество G(x). Отображение G в этом случае будет являться многозначным отображением.
Отображение является, таким образом, всюду определенным отношением и определяется тройкой множеств (X,Y,G).
Интересным является случай, когда множества XиYсовпадают:X=Y. ОтображениеG:XXпредставляет собой отображение множестваXсамого в себя и определяется парой множеств (X,G), гдеGXX. Подробным изучением таких отображений занимается теория графов. Рассмотрим здесь лишь нескольких операций над ними.
Пусть G и Н – отображения множества X в X. Композицией этих отображений назовем отображение GH, которое определяется следующим образом:
GH(x) =G(H(x)).
В частном случае при Н = Gполучим отображения:
G2(x) =G(G(x)),G3(x) =G(G2(x)) и т. д.
Для произвольного S2 имеем:GS(x) =G(GS -1(x)).
Введем для общности соотношение: G0(x) = х. Тогда можно записать:
G0(x) =G(G-1(x)) =GG-1(x) = х.
Это означает, что G-1(x) представляет собой обратное отображение. ТогдаG-2(x) =G-1(G-1(x)) и т. д.
Пример. Пусть X – множество людей. Для каждого человека х X обозначим через G(x) множество его детей. Тогда:
G2(x) – множество внуков х,
G3(x) – множество правнуков х,
G-1(х) – множество родителей х и т. д.
Изображая людей точками и рисуя стрелки, идущие из х в G(x), получим родословное, или генеалогическое дерево, представленное на рис. 1.10.
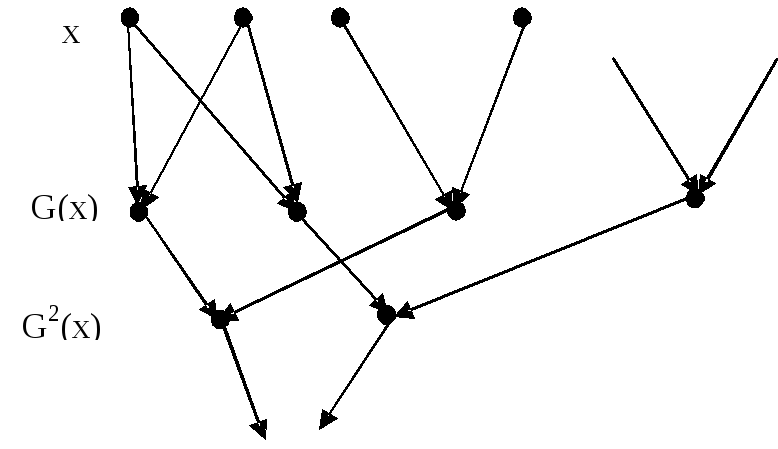
Рис. 1.10. Генеалогическое дерево
1.7. Контрольные вопросы и упражнения
Вставьте обозначения числовых множеств:
м
 ножество
натуральных чисел;
ножество
натуральных чисел;множество целых чисел;
множество рациональных чисел;
множество действительных чисел.
2. Вставьте пропущенный знак или : 117 ___ N; 22,4 ___ Z; 4/3___Q;
![]() ___ Q;
___ Q; ![]() ___R;
___ Z.
___R;
___ Z.
Принадлежит ли множеству корней уравнения
x2 - 5х + 6 = 0 число х = -3?
Какими способами можно задать множество?
Запишите множество действительных корней уравнения 3х + 4 = 0. Как записать ответ, если требуется найти множество целых корней этого уравнения?
Что такое подмножество данного множества? Какой символ используется для записи «множество А является подмножеством множества В»? Запишите его: А ____ В.
Вставьте пропущенный символ или :
1 ___ {1,2,3}; {1} ____ {1,2,3};
___ {1,2,3}; {2,3} ____ {1,2,3}.
Вставьте пропущенные знаки операций на множествах:
{а,b,с} ____ {d,b,e} = {b};
{a,b,с} ____ {с, d} = {а,b,с,d};
{а,b,с} ____ {a,d} = {b,c}.
Что такое булеан множества X?
Я
 вляется
ли булеаном множества {а,b,с} система
подмножеств {а}, {b}, {с} ?
вляется
ли булеаном множества {а,b,с} система
подмножеств {а}, {b}, {с} ?Я
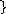 вляется
ли разбиением множества {а,b,с} система
подмножеств {a,b},{b,с},{а,с} ?
вляется
ли разбиением множества {а,b,с} система
подмножеств {a,b},{b,с},{а,с} ?Нарисуйте диаграммы Эйлера для левой и правой частей закона де Моргана. Сравните их.
Запишите законы алгебры множеств. Запомните их названия.
Вставьте пропущенный знак = или : {3,5} _____ {5,3}; (3,5) _____ (5,3).
Нарисуйте график декартова произведения X Y, где X = {1,5}, Y = {2,3}. Совпадает ли он с графиком У X?
Дайте определение бинарного отношения на множестве.
Обведите кружком номер правильного ответа. Областью определения бинарного отношения R называется множество
а) {(х, у)| (х, у) R};
б) {х| (х, у) R};
в) {у| (х, у) R}.
Какими способами можно задать бинарное отношение?
Какое отношение является рефлексивным?
Какой особенностью обладает матрица рефлексивного отношения? А матрица симметричного отношения?
Закончите фразу: Отношение, обладающее свойствами рефлексивности, симметричности, транзитивности, называется отношением
_________________________________________.
Запись [х] используется для обозначения __________________________________________.
2. Математическая логика
2.1.Алгебра логики
2.1.1. Логические высказывания
Под логическим высказываниемпонимается повествовательное предложение, о котором имеет смысл говорить, что оно истинно или ложно, но не то и другое вместе.
Примеры:
Волга впадает в Каспийское море.
Два больше трёх.
Я лгу.
Примеры 1, 2 являются высказываниями (1 – истинно, 2 –ложно). Пример 3 – не высказывание (если предположить, что оно истинно, то в силу его смысла оно одновременно ложно и, наоборот, из ложности этого предложения вытекает его истинность).
В алгебре логики не рассматривают внутреннюю структуру высказываний, а ограничиваются рассмотрением их свойства представлять истину или ложь. Поэтому на высказывание можно смотреть, как на величину, которая может принимать только одно из двух значений: «истина» или «ложь».
Высказывания будем обозначать буквами А, В, С, а их значения («истина» или «ложь») – соответственно цифрами 1 или 0. Эти цифры будем рассматривать как символы, не имеющие арифметического смысла.
В обычной речи сложные предложения образуются из простых предложений с помощью связок: «и», «или», «если..., то…» и т. д.
Примеры:
Светит солнце, и идёт дождь.
Шесть делится на два или шесть делится на три.
Если контакт замкнут, то лампа горит.
Связкиможно рассматривать какоперациинад высказываниями. В алгебре логики вводят операции, аналогичные связкам обычной речи. При этом истинность или ложность сложного высказывания полностью определяется истинностью или ложностью его составляющих.
2.1.2. Основные логические операции
1. Выражение А В(«А и В») означает высказывание, истинное только в том случае, когда А и В истинны.
Такое высказывание называют конъюнкцией высказыванийА и В. Символобозначает операцию конъюнкции. Эта операция соответствует союзу«и»в обычной речи. В алгебре логики знак операции «» можно опускать или заменять на «•».
В обычной речи не принято соединять союзом «и» два высказывания, далекие по содержанию. В алгебре высказываний операция конъюнкции может быть применена к любым двум высказываниям. Например, для высказываний: «пять больше трех» и «трава зеленая» их конъюнкция является истинным высказыванием.
2. Выражение А В(«А или В») означает высказывание, истинное, если хотя бы одно из высказываний А или В является истинным.
Такое высказывание называют дизъюнкцией высказыванийА и В. Символобозначает операцию дизъюнкции. Эта операция соответствует союзу «или» в обычной речи, применяемому в неисключающем смысле.
Дело в том, что в обычной речи союз «или» может иметь два смысловых значения: неисключающее и исключающее. В первом случае подразумевается, что из двух высказываний, по крайней мере, одно истинно, а может быть и оба истинны. Пример такого высказывания: «В жаркую погоду пьют воду или едят мороженое». Во втором случае полагают, что из двух высказываний истинным является только одно. Пример такого высказывания: «Сегодня мы поедем на экскурсию или пойдем на пляж». Конъюнкция высказываний соответствует первому случаю.
3. Выражение A B(«если А, то В» или «А влечет В») означает высказывание, которое ложно тогда и только тогда, когда А истинно, а В ложно.
Такое высказывание называют импликацией высказыванийА и В. Высказывание А называетсяусловием(посылкой), высказывание В –заключением(следствием) импликации. Символобозначает операцию импликации.
В обычной речи операции импликации соответствует связка «если ..., то…». Отличие состоит в том, что связка предполагает смысловую зависимость соединяемых высказываний, а для операциисмысловая связь несущественна.
Например, высказывания: «если 2 * 2 = 5, то трава синяя» и «если два больше трех, то восемь делится на четыре» являются истинными, так как у первого из них ложная посылка, а у второго – истинное следствие. Импликация: «если 2 * 2 = 4, то 5 < 2» ложна, поскольку ее условие истинно, а заключение ложно.