ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.08.2024
Просмотров: 1778
Скачиваний: 0
СОДЕРЖАНИЕ
1.4. Декартово произведение множеств
1.5.1. Определение бинарного отношения
1.5.2. Способы задания бинарного отношения
1.5.3. Свойства бинарных отношений
1.5.4. Отношения эквивалентности
1.7. Контрольные вопросы и упражнения
2.1.1. Логические высказывания
2.1.2. Основные логические операции
2.2.1. Булевы функции и операции
2.2.2. Совершенные дизъюнктивная и конъюнктивная нормальные формы
2.3. Полные системы логических функций
Класс функций, сохраняющих ноль
Класс функций, сохраняющих единицу
Класс самодвойственных функций
2.4.3. Минимизация днф методом Квайна
2.6. Контрольные вопросы и упражнения
3.1.2. Ориентированные и неориентированные графы
3.1.4. Частичные графы и подграфы
3.1.6. Изоморфизм. Плоские графы
3.2. Отношения на множествах и графы
3.3. Матрицы смежности и инциденций графа
3.5.1. Степени неориентированных графов
3.5.2. Степени ориентированных графов
3.6.1. Характеристики расстояний в графах
3.6.2. Характеристические числа графов
3.7.2 . Базисные циклы и разрезающие множества
Свойства базисных циклов и разрежающих множеств
3.7.3. Цикломатическая матрица и матрица разрезов
Составление цикломатической матрицы
3.8. Задача определения путей в графах
3.8.1. Определение путей в графе
3.8.2. Алгоритм определения кратчайших путей
2.2.2. Совершенные дизъюнктивная и конъюнктивная нормальные формы
Рассмотрим возможность представления произвольной функции в виде булевой формулы, содержащей только операции дизъюнкции, конъюнкции и отрицания.
Теоремы 1 и 2 доказывают возможность такого представления. Введем некоторые понятия.
Элементарной
конъюнкцией (ЭК) называется выражение
![]() где
все
где
все
![]() –
различны, аr–ранг
конъюнкции. Функция-константа единица
(Ui=
1) считается конъюнкцией нулевого ранга.
–
различны, аr–ранг
конъюнкции. Функция-константа единица
(Ui=
1) считается конъюнкцией нулевого ранга.
Элементарной
дизъюнкцией
(ЭД) называется выражение
![]() где все
где все
![]() –
различны, а r
– ранг
дизъюнкции.
Функция-константа единица (Ui
=
0) считается дизъюнкцией нулевого ранга.
–
различны, а r
– ранг
дизъюнкции.
Функция-константа единица (Ui
=
0) считается дизъюнкцией нулевого ранга.
Дизъюнктивной нормальной формой(ДНФ) называется дизъюнкция N =U1 U2 ...Ukэлементарных конъюнкцийU1,U2, ...,Uk. Совершенная ДНФ – частный случай ДНФ, элементарные конъюнкции которой содержат все переменные и ранг их равенn.
Конъюнктивной нормальной формой (КНФ) называется конъюнкция N = U1 U2 ... Uk элементарных дизъюнкций U1, U2, ..., Uk. Совершенная КНФ – частный случай КНФ, элементарные дизъюнкции которой содержат все переменные и ранг их равен n.
Теорема 1. Произвольную логическую функцию f(х1, х2, ..., хn) можно представить в виде
![]() (2)
(2)
где σi {0, 1}, xi0 =хi, xi1 = xi, σ = (σ1, …, σn) и дизъюнкция берётся по всем n-мерным наборам из нулей и единиц.
Доказательство. Покажем, что левая и правая части соотношения (2) совпадают. Подставим в (2) произвольный набор α = (α1, …, αn), где каждое αi {0,1}. В левой части получим f(α1, α2, …, αn), а в правой части:
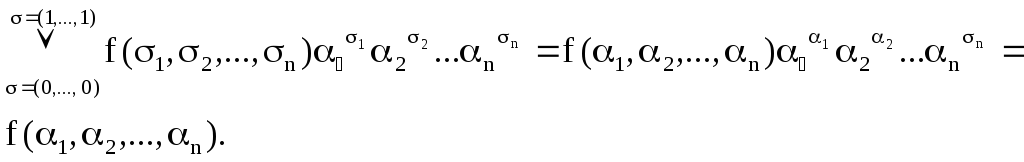 Равенства
в правой части вытекают из свойств
конъюнкции, дизъюнкции и из того,
что: хσ
= 1
х = σ.
Равенства
в правой части вытекают из свойств
конъюнкции, дизъюнкции и из того,
что: хσ
= 1
х = σ.
Если f(х1, х2,..., хn)≢0, то соотношение (2) можно переписать в форме:
![]() (3)
(3)
Эта формула (3) называется совершенной дизъюнктивной нормальной формой (СДНФ) функции f(x1, х2,..., xn).
Следствие. Для произвольной логической функции существует взаимнооднозначное соответствие между ее СДНФ и таблицей истинности:
а) СДНФ содержит ровно столько элементарных конъюнкций, сколько единичных наборов у функции;
б) каждому единичному набору σ = (σ1, …, σn) соответствует элементарная конъюнкция всех переменных функции, в которой для σi= 0 переменная хi берется с отрицанием и для σi= 1 – без отрицания.
Рассмотрим
построение СДНФ по таблице истинности
функции f(x1,
х2, ...,xn).
Для каждого набора σ = (σ1, …, σn)
из единичного множества [1] (такого,
чтоf(σ1, …, σn)
= 1), составляется выражение ЭК:
![]() .
Затем эти конъюнкции соединяются знаком
дизъюнкции.
.
Затем эти конъюнкции соединяются знаком
дизъюнкции.
Пример 1. Построим СДНФ для функции неэквивалентности f7(x1, х2)=(х1 х2). Исходя из единичного множества этой функции [1] = {(0, 1), (1, 0)} формула СДНФ будет иметь вид: FСДНФ = х1 • х2 х1•х2.
Теорема 2. Произвольную логическую функцию f (х1, х2,..., хn) можно представить в виде:
![]() (4)
(4)
г
и конъюнкция берётся по всем n-мерным наборам из нулей и единиц.
Доказательство.
Из свойства булевой функции имеем
f
(х1,
х2,...,
хn)
=
![]() (х1,
х2,
..., хn).
Для функции f(х1,
х2,...,
хn)
по теореме 1 существует представление
в виде
(х1,
х2,
..., хn).
Для функции f(х1,
х2,...,
хn)
по теореме 1 существует представление
в виде
![]()
тогда имеем:
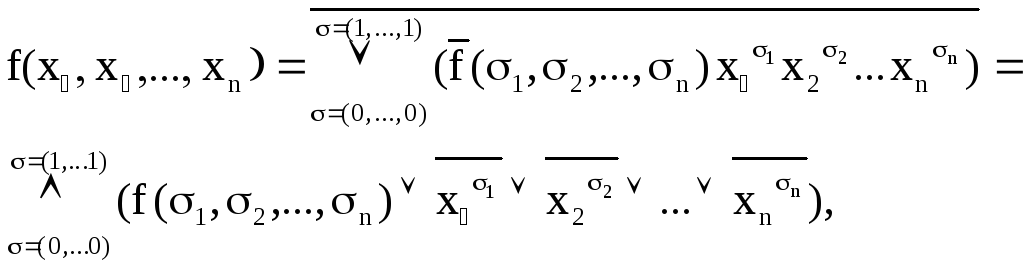
что следует из закона де Моргана.
Заметим также, что
![]() .
Следовательно,
.
Следовательно,
![]()
Если f(х1, х2, ..., хn) ≢ 1, то соотношение (4) можно переписать в форме
![]() (5)
(5)
Эта форма называется совершенной конъюнктивной нормальной формой (СКНФ).
Следствие. Для произвольной логической функции также существует взаимнооднозначное соответствие между ее СКНФ и таблицей истинности:
а) СКНФ содержит ровно столько элементарных дизъюнкций, сколько нулевых наборов у функции;
б) каждому нулевому набору σ = (σ1, …, σn) соответствует элементарная дизъюнкция всех переменных функции, в которой для σi = 1 переменная хi берется с отрицанием и для σi = 0 – без отрицания.
Рассмотрим
построение СКНФ по таблице истинности
функции f(x1,
х2,...,
xn).
Для каждого набора σ = (σ1,
…, σn)
из нулевого множества [0] (такого, что
f(σ1,
…, σn)
= 0), составляется выражение ЭД:
![]() .
Затем эти дизъюнкции соединяются знаком
конъюнкции.
.
Затем эти дизъюнкции соединяются знаком
конъюнкции.
Пример 2. Построим СКНФ для функции неэквивалентности f7(x1, х2) = (х1 х2). Исходя из нулевого множества этой функции [0] = {(0, 0), (1, 1)} формула СКНФ будет иметь вид: FСКНФ = (х1 х2) • (х1 х2).
2.3. Полные системы логических функций
Система функций = {f1(x11,...,x1p1), ..., fs(xs1, ...,xsps),…} называетсяполной, если любую логическую функциюf(x1, ...,xn) можно представить в виде суперпозиции функций {f1, ...,fs, ...} и переменных х1, ..., хn.
Функции, входящие в полную систему, называются базисными, а сама полная система функций –базисом.
Примеры полных систем функций (базисов)
1. Булевый базис 0= {х1• х2,x1х2,х}.
Полнота булева базиса следует из того, что для любой логической функции можно построить СДНФ или СКНФ.
2
x1 х2=х1•х2.
3. Дизъюнктивный булевый базис 2= {x1 х2,х }.
П
х1 • х2 =х1 х2.
4. Базис Жегалкина 3 = {х1 • х2, х1 х2, 1}.
Полнота этого базиса следует из п. 2 и представления отрицания в виде:х = х 1.
Теорема 3. Любую логическую функциюf(x1, ...,xn) можно представить в виде полинома Жегалкина:
f(x1, ...,xn) = а0а1x1а2x2…а2n-1x1…xn, (6)
где аi {0,1}, i = 0, 1, ..., 2n - 1.
Доказательство.Система функций= {х1• х2, х1х2, 1, 0} полна. Из формулы СДНФ (3), пользуясь свойствами:
xx= 0,x•x=x,x0 =x,
x• 0 = 0,x• 1 =x,x1•x2=x2•x1,
x1 x2 = x2 x1, (x1 x2) • x3 = (x1 • x3) (x2 • x3),
получим представление функции в виде полинома (6).
Следствие. Для любой логической функции, наряду с СДНФ и СКНФ в случае булева базиса, существует единственный полином Жегалкина вида (6).
Далее в теореме 4 формулируется критерий полноты системы логических функций, на основе которого можно проверить полноту данной системы функций, а также построить другие базисы.
Теорема 4 (о полноте). Для того чтобы система функций {f1(xl1 ..., х1р1), ...,fs(xs1, ...,xsps), ...} была полна, необходимо и достаточно, чтобы она содержала функцию, не сохраняющую 0; функцию, не сохраняющую 1; несамодвойственную функцию; немонотонную функцию; нелинейную функцию.
Класс функций, сохраняющих ноль
Функция f(х1, ..., хn) называется сохраняющей ноль, если она на нулевом наборе принимает значение 0, то естьf(0, ..., 0) = 0.
Пример.f(х) = 0,f(х) = х,f(х1, х2) = х1• х2,f(х1, х2) = х1Úх2 сохраняют ноль;f(х) = 1,f(х) =х,f(х1, х2) = х1® х2 не сохраняют ноль.
Лемма 1. Из функций, сохраняющих ноль, суперпозицией можно получить только функции, сохраняющие ноль.
Доказательство. Функции, равные переменным, сохраняют ноль. Поэтому достаточно показать, что функция
Ф(х1, ..., хn) = f(f1(х1, ..., хn), ..., fm(х1, ..., хn))
сохраняет ноль, если функции f, fl, …, fm сохраняют ноль. Последнее следует из
f(f1(0, ..., 0), ... fm(0, ..., 0)) = f(0, ..., 0) = 0.
Следствие. Полная система функций должна содержать хотя бы одну функцию, не сохраняющую ноль.
Класс функций, сохраняющих единицу
Функция f(х1, ..., хn) называется сохраняющей единицу, если она на единичном наборе принимает значение 1, то естьf(1, ..., 1) = 1.
Пример.Функцииf(х) = 1,f(х) = х – сохраняют единицу; функцииf(х) = 0,f(х) =х,f(х1, х2) =х1 Å х2 – не сохраняют единицу.
Лемма 2. Из функций, сохраняющих единицу, суперпозицией можно получить только функции, сохраняющие единицу. Доказательство очевидно.
Следствие. Полная система функций должна содержать хотя бы одну функцию, не сохраняющую единицу.