Добавлен: 21.10.2018
Просмотров: 3247
Скачиваний: 12
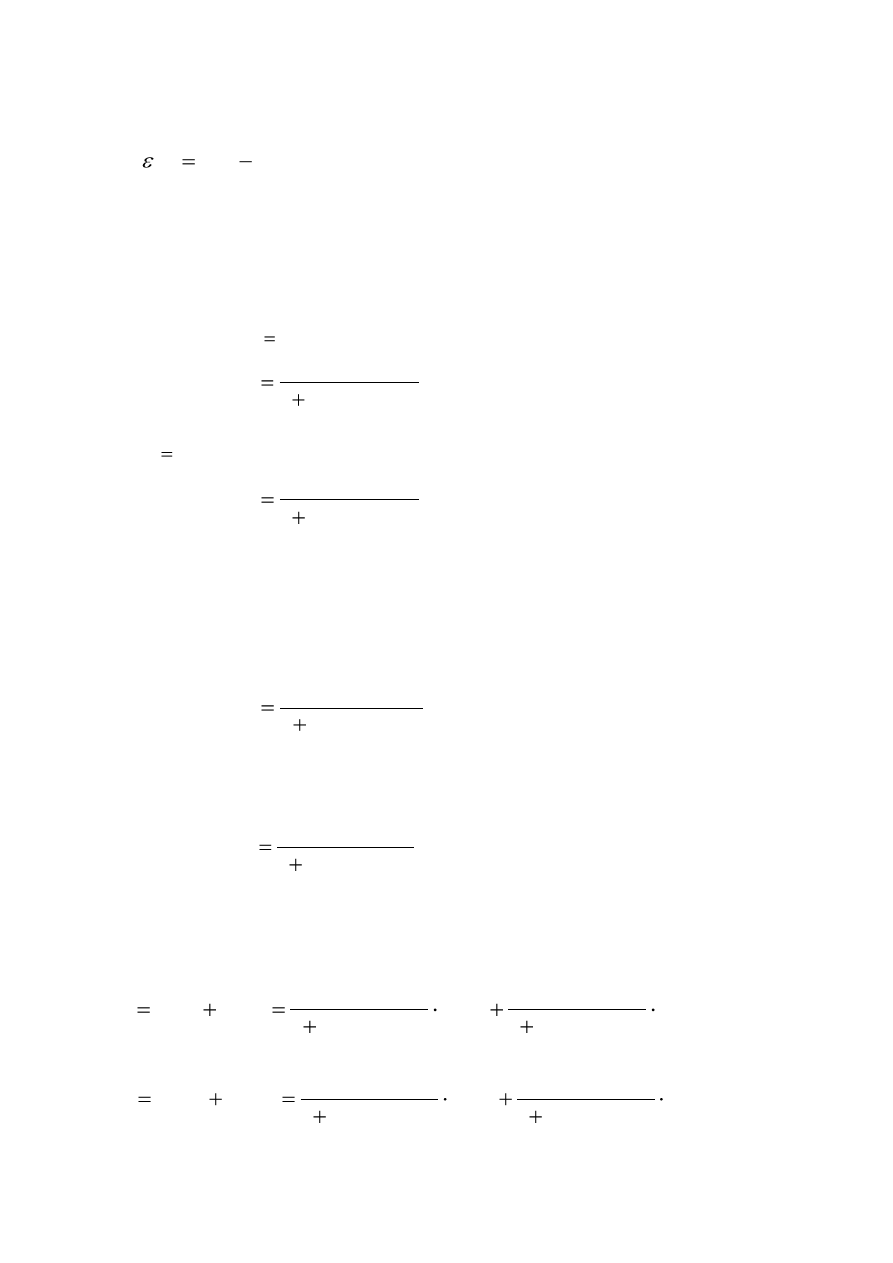
13
y(t)
- выходной сигнал;
)
(t
f
- возмущающее воздействие или помеха;
)
(
)
(
)
(
ОС
t
y
t
x
t
- ошибка системы;
)
(s
W
- передаточная функция прямой цепи;
)
(
ОС
s
W
- передаточная функция обратной связи;
)
(s
W
f
- передаточная функция канала помехи или возмущающего
воздействия.
Передаточная функция замкнутой САУ по управляющему воздействию
запишется при
0
)
(t
f
:
)
(
)
(
1
)
(
)
(
ОС
s
W
s
W
s
W
s
W
yx
(1)
Передаточная функция замкнутой САУ по возмущающему воздействию
при
0
)
(t
x
:
)
(
)
(
1
)
(
)
(
ОС
s
W
s
W
s
W
s
W
f
yf
(2)
Для определения точности САУ в установившемся режиме необходимо
знание передаточных функций по ошибке.
Передаточная функция по ошибке замкнутой САУ
по управляющему воздействию:
)
(
)
(
1
1
)
(
ОС
s
W
s
W
s
W
ex
(3)
по возмущающему воздействию
)
(
)
(
1
)
(
)
(
ОС
s
W
s
W
s
W
s
W
f
ef
(4)
Используя принцип суперпозиции и (1) - (4), определим выходной сигнал
системы и ошибку в изображениях Лапласа:
)
(
)
(
)
(
1
)
(
)
(
)
(
)
(
1
)
(
)
(
)
(
)
(
ОС
ОС
s
F
s
W
s
W
s
W
s
X
s
W
s
W
s
W
s
Y
s
Y
s
Y
f
f
x
(5)
)
(
)
(
)
(
1
)
(
)
(
)
(
)
(
1
)
(
)
(
)
(
)
(
ОС
ОС
s
F
s
W
s
W
s
W
s
X
s
W
s
W
s
W
s
E
s
E
s
E
f
f
x
(6)
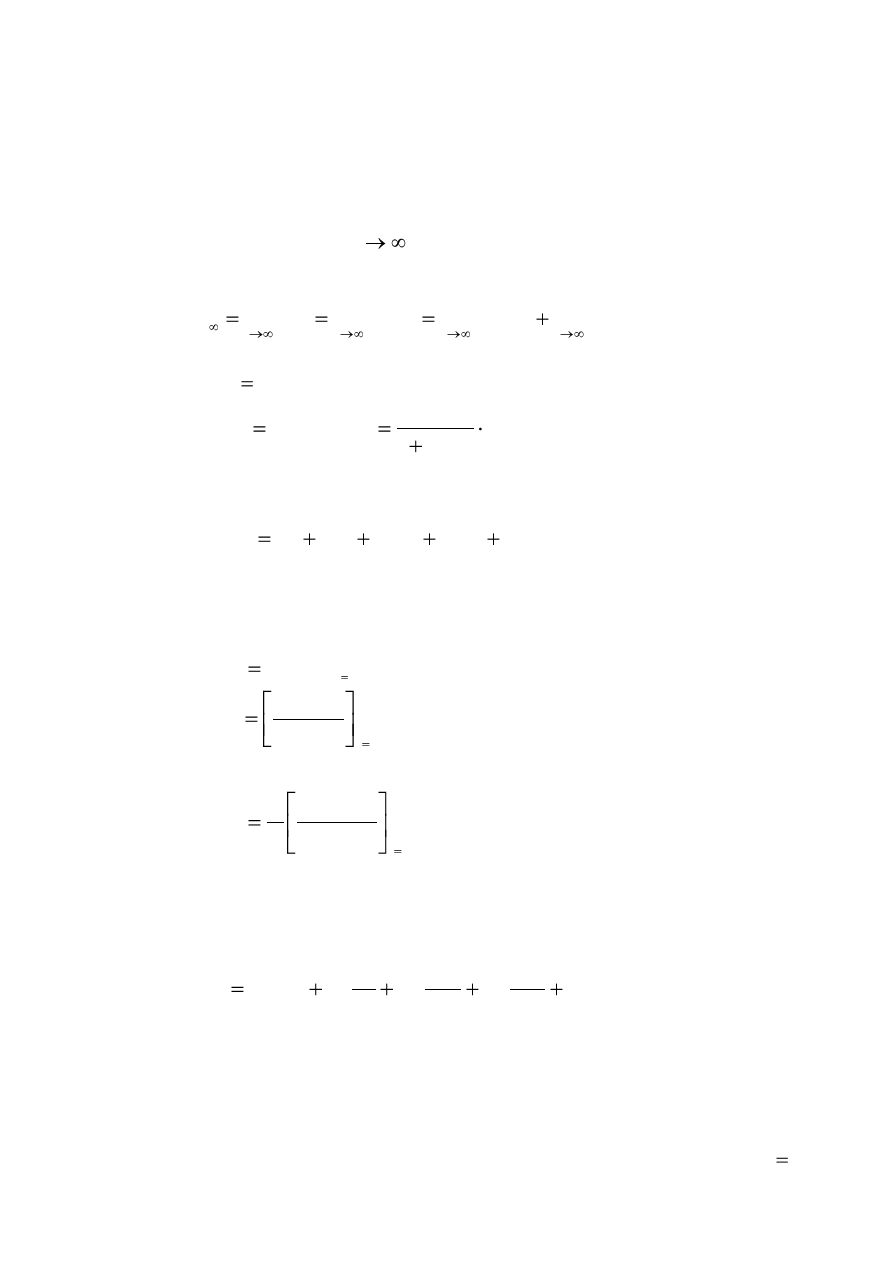
14
2.3. Статическая точность САУ при произвольных
и типовых воздействиях
.
Одним из основных требований, предъявляемых к САУ, является
обеспечение
статической
точности
управляющего
воздействия
в
установившемся режиме при
t
.
На основе теоремы о конечном значении функции в преобразованиях
Лапласа можно написать:
)
(
lim
)
(
lim
)
(
lim
)
(
lim
e
s
sE
s
sE
s
sE
t
e
f
s
x
s
s
t
(7)
Если
1
)
(
ОС
s
W
, то изображение ошибки по управляющему воздействию:
)
(
)
(
1
1
)
(
)
(
)
(
s
X
s
W
s
X
s
W
s
E
ex
x
.
(8)
)
(s
W
ex
выражается в виде ряда по степеням S.
Тогда:
...
)
(
3
3
2
2
1
0
S
C
S
C
S
C
C
s
W
ex
(9)
где коэффициенты ряда, которые называются коэффициентами ошибок,
определяются как:
0
0
1
0
0
)
(
!
1
...
)
(
)]
(
[
s
n
ex
n
n
s
ex
s
ex
ds
s
W
d
n
C
ds
s
dW
C
s
W
C
(10)
Преобразуя зависимость (8) во временную область с учётом (9), определим
выражение ошибки при произвольном входном сигнале:
...
)
(
)
(
3
3
3
2
2
2
1
0
dt
x
d
C
dt
x
d
C
dt
dx
C
t
x
C
t
e
.
(11)
Аналогичную зависимость можно получить и для ошибки по
возмущающему воздействию
)
(
e
f
t .
На основе общих выражений (6) определим установившиеся ошибки при
типовых управляющих и возмущающих воздействий для САУ с единичной
обратной связью, то есть при единичной обратной связи
1
)
(
ОС
s
W
.

15
Рассмотрим следующие варианты типовых воздействий:
a)
const
x
t
x
0
)
(
,
const
f
t
f
0
)
(
.
Используя зависимости (6) и (7), получим статическую ошибку при
t
0
0
)
(
1
)
0
(
)
0
(
1
1
f
s
W
W
x
W
e
e
e
f
f
x
(12)
Для статических САУ, где
k
W
)
0
(
:
k
e
x
1
x
0
,
f
f
f
k
f
k
e
1
0
,
(13)
где k - коэффициент передачи разомкнутой системы;
f
k
- коэффициент передачи системы по возмущению разомкнутой системы.
Для астатических систем -
)
0
(
W
, поэтому:
0
x
e
.
(14)
Если
const
k
f
, то и
0
f
e
.
б)
t
x
t
x
0
)
(
, где
const
x
0
,
const
f
t
f
0
)
(
.
На основе зависимости (12):
)
(
1
)
(
lim
)
(
1
lim
0
0
0
0
s
W
f
s
W
s
W
s
x
e
f
s
s
.
(15)
Для систем с астатизмом первого порядка скоростная ошибка по
управляющему воздействию с постоянной скоростью
0
0
x
k
e
x
,
(16)
где
)
0
(
lim
0
sW
k
s
- коэффициент передачи и добротность системы по
скорости.
Для системы с астатизмом второго порядка и выше скоростная ошибка
0
x
e
. Поэтому типовой сигнал
t
x
t
x
0
)
(
используется только для оценки
точности астатических систем первого порядка.
в)
2
)
(
2
0
t
x
t
x
, где
const
x
0
,
const
f
t
f
0
)
(
.
Аналогично:
)
(
1
)
(
lim
)
(
1
lim
0
0
2
0
0
s
W
f
s
W
s
W
s
x
e
f
s
s
.
(17)
Для систем с астатизмом второго порядка ошибка ускорения по
управляющему воздействию:

16
a
x
k
0
x
,
(18)
где
)
(
lim
2
s
s
W
s
k
a
- коэффициент передачи или добротность системы
по ускорению.
Второе слагаемое выражения (12) как и в предыдущем случае определяет
статическую ошибку по возмущающему воздействию.
г)
t
x
t
x
0
0
sin
)
(
,
0
)
(t
f
.
В установившемся режиме ошибка по управляющему воздействию:
)
sin(
)
(
0
0
t
t
x
.
Подставив
j
s
в (12) при
0
)
(t
f
, получим
)
(
1
)
(
0
0
0
0
0
j
W
x
j
W
x
ex
.
(19)
При
1
)
(
0
j
W
:
)
(
0
0
0
j
W
x
.
В итоге, на основе вышеполученных зависимостей определяются
параметры САУ, т.е. коэффициенты добротности, обеспечивающие ошибки
x
e
и
f
e в установившемся режиме.
2.4. Обоснование построения желаемой ЛАЧХ
Одним из наиболее распространенных методов синтеза корректирующих
устройств является метод В.В.Солодовникова, предполагающий построение
желаемой логарифмической амплитудно-частотной характеристики ЛАЧХ,
исходя из требуемых показателей качества. Для этого используют однозначную
зависимость
для
минимально-фазовых
систем
между
параметрами,
определяющими качество переходного процесса при единичном входном
воздействии, и видом вещественной частотной характеристики замкнутой
системы
)
(
З
P
.
В качестве исходной вещественной частотной характеристики
)
(
Т
З
P
принимается типовая характеристика, представленная на рис.7.
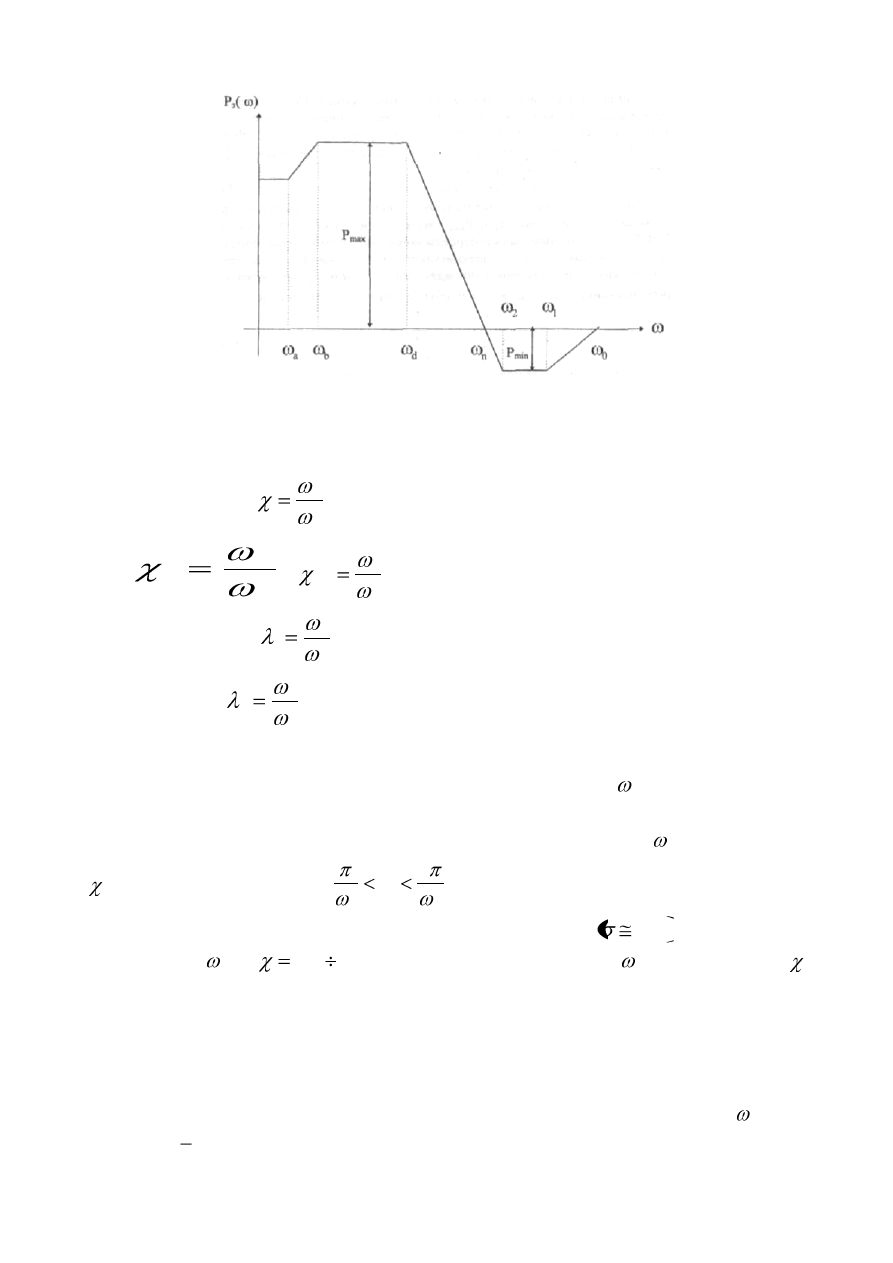
17
Рис. 7. Типовая вещественная частотная характеристика
Форму этой характеристики определяют:
n
d
- основной коэффициент наклона;
n
d
,
0
1
2
g
- дополнительный коэффициент наклона;
n
b
1
- основной коэффициент формы;
0
2
2
- дополнительный коэффициент формы.
Эти коэффициенты однозначно определяют
max
P
и
min
P
.
В свою очередь типовые характеристики
)
(
З
P
с различными
коэффициентами наклона и формы соответствуют различным переходным
процессам. В [2] показано, что время регулирования
P
t для
)
(
З
P
с различными
находится в пределах
0
0
4
P
t
, а наименьшее время
P
t переходного
процесса при незначительном его перерегулировании
%
4
соответствует
типовым
)
(
Т
З
P
с
25
,
0
2
,
0
. Там же для типовых
)
(
Т
З
P
с различными
построены номограммы, с помощью которых установлена функциональная
связь запасов устойчивости по амплитуде и фазе с наклонами ЛАЧХ
разомкнутых систем в диапазоне средних частот.
Согласно этим номограммам следует, что ЛАЧХ разомкнутой САУ,
которая соответствует требуемым типовым характеристикам переходного
процесса, должна пересекать ось абсцисс в точке частоты среза
С
под
наклоном
дБ/дек
20
.