Добавлен: 21.10.2018
Просмотров: 3251
Скачиваний: 12

23
W
ky
(s)
)
(s
Y
)
(s
X
W
н
(s)
)
(t
x
)
(t
y
Рис. 10. Структурная схема САУ с последовательным корректирующим звеном.
)
(s
W
ky
- передаточная функция передаточного звена;
)
(s
W
H
- передаточная функция неизменяемой части САУ.
Передаточная функция желаемой разомкнутой САУ:
)
(
)
(
)
(
s
W
s
W
s
W
ky
H
(30)
Откуда ЛАЧХ последовательного корректирующего звена имеет вид:
)
(
lg
20
)
(
lg
20
)
(
lg
20
j
W
j
W
j
W
H
ky
(31)
Фазочастотная характеристика последовательного корректирующего звена:
)
(
)
(
)
(
H
ky
.
(32)
Выражения (31) и (32) показывают, что для определения ЛАЧХ
последовательного корректирующего звена необходимо:
1. Построить ЛАЧХ неизменяемой части разомкнутой системы;
2. Построить по заданным показателям качества желаемую ЛАЧХ разомкнутой
системы
)
(
lg
20
j
W
;
3. Вычесть из желаемой ЛАЧХ характеристику неизменяемой части системы
согласно (31);
4. По виду ЛАЧХ корректирующего звена определить его передаточную
функцию и схему.
б). Синтез параллельного корректирующего звена
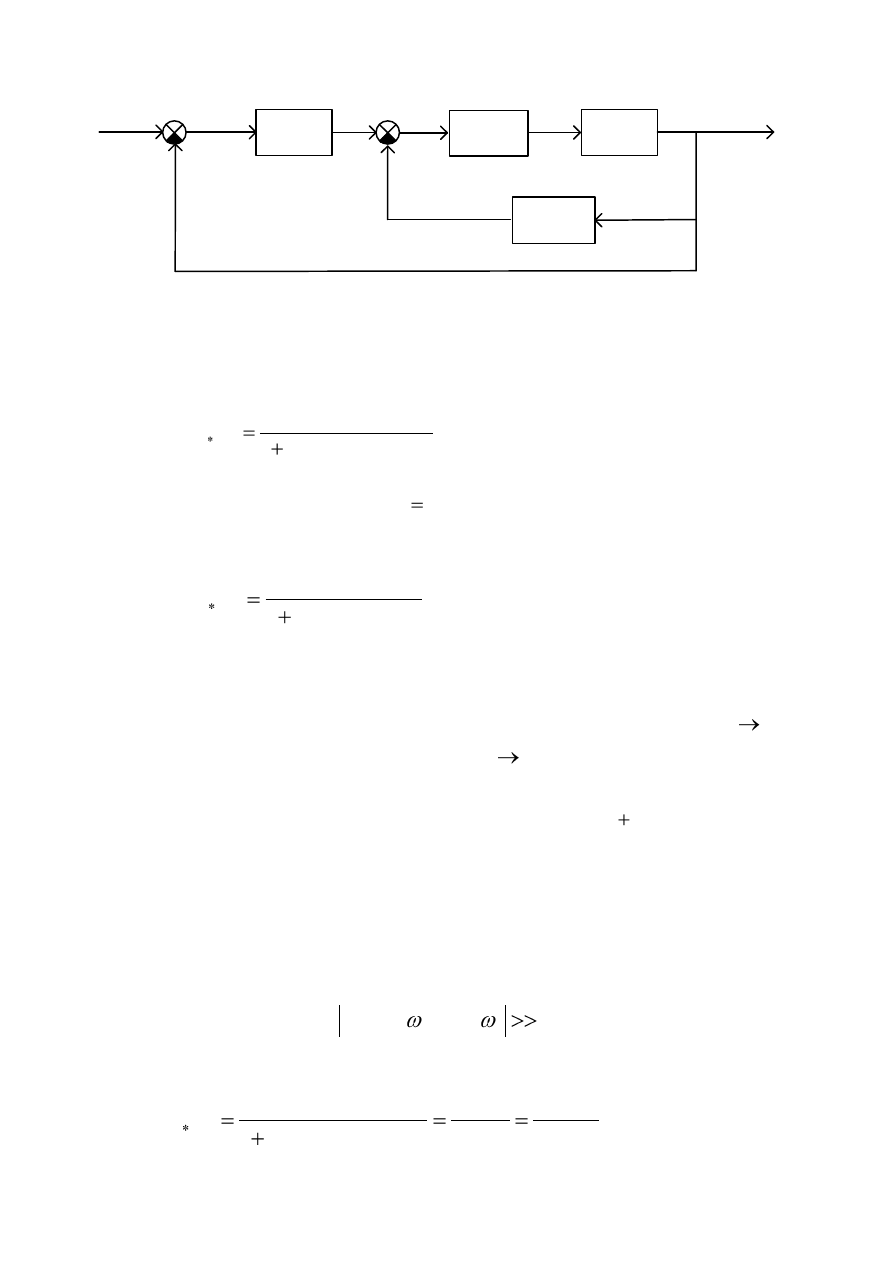
Структурная схема САУ с параллельным корректирующим звеном,
охватывающим в виде обратной связи часть последовательных звеньев
системы, представлена на рис.11.
24
W
1
(s)
W
2
(s)
W
3
(s)
W
ky
(s)
)
(s
X
)
(t
x
)
(s
Y
)
(t
y
Рис. 11. Структурная схема САУ с параллельным корректирующим звеном.
Передаточная функция скорректированной разомкнутой системы является
желаемой передаточной функцией, т. е.
)
(
)
(
)
(
1
)
(
)
(
)
(
)
(
3
2
3
2
1
s
W
s
W
s
W
s
W
s
W
s
W
s
W
ky
(33)
Если обозначить
)
(
)
(
)
(
ОХВ
3
2
s
W
s
W
s
W
, тогда передаточная функция
внутреннего контура:
)
(
)
(
1
)
(
)
(
s
W
s
W
s
W
s
W
ky
ОХВ
ОХВ
(34)
В астатических системах следует учитывать особенности действия
обратной связи. Чтобы вводимая обратная связь не понижала порядок
астатизма системы, необходимо иметь порядок нулей
)
(s
W
ky
при
0
S
не
ниже порядка полюсов
)
(s
W
ОХВ
при
0
S
. Если кратность полюсов
)
(s
W
ОХВ
равна кратности нулей
)
(s
W
ky
, то общий коэффициент усиления
системы после введения обратной связи уменьшится в
)
1
(
ОХВ
K
K
ky
раз. Если
кратность полюсов
)
(s
W
ОХВ
меньше кратности нулей
)
(s
W
ky
, то общий
коэффициент усиления системы при введении обратной связи остается
неизменным.
Выбор
)
(s
W
ky
этого типа с помощью ЛАЧХ выполняется для тех
диапазонов частот, для которых справедливо неравенство:
1
)
(
)
(
ОХВ
j
W
j
W
ky
.
Тогда выражение (33) преобразуется:
)
(
)
(
)
(
)
(
)
(
)
(
)
(
1
)
(
)
(
)
(
)
(
НХ
1
3
2
3
2
1
s
W
s
W
s
W
s
W
s
W
s
W
s
W
s
W
s
W
s
W
s
W
ky
ky
ky
,
(35)
25
где
)
(
)
(
1
НХ
s
W
s
W
- передаточная функция звеньев неохваченных
)
(s
W
ky
.
Откуда
(s)
W
)
(
)
(
НХ
s
W
s
W
ky
или, переходя к ЛАЧХ, определяем характеристику
параллельного корректирующего звена:
)
(
lg
20
)
(
lg
20
)
(
lg
20
)
(
lg
20
)
(
lg
20
)
(
lg
20
ОХВ
НХ
j
W
j
W
j
W
j
W
j
W
j
W
ky
(36)
На основании полученных выражений для определения параллельного
корректирующего звена
)
(s
W
ky
необходимо:
1. Построить ЛАЧХ неохваченной части системы
)
(
lg
20
j
W
НХ
;
2. Построить по заданным показателям качества желаемую ЛАЧХ разомкнутой
системы
)
(
lg
20
j
W
;
3. Вычесть из ЛАЧХ неохваченной системы желаемую ЛАЧХ;
4. По виду ЛАЧХ корректирующего звена определить его передаточную
функцию и предложить схему реализации.
в). Синтез последовательного и параллельного корректирующих звеньев
В некоторых случаях, когда два предыдущих способа синтеза
корректирующих звеньев приводят к сложным схемным решениям, возникает
необходимость их разбиения на последовательное и параллельное
корректирующие звенья.
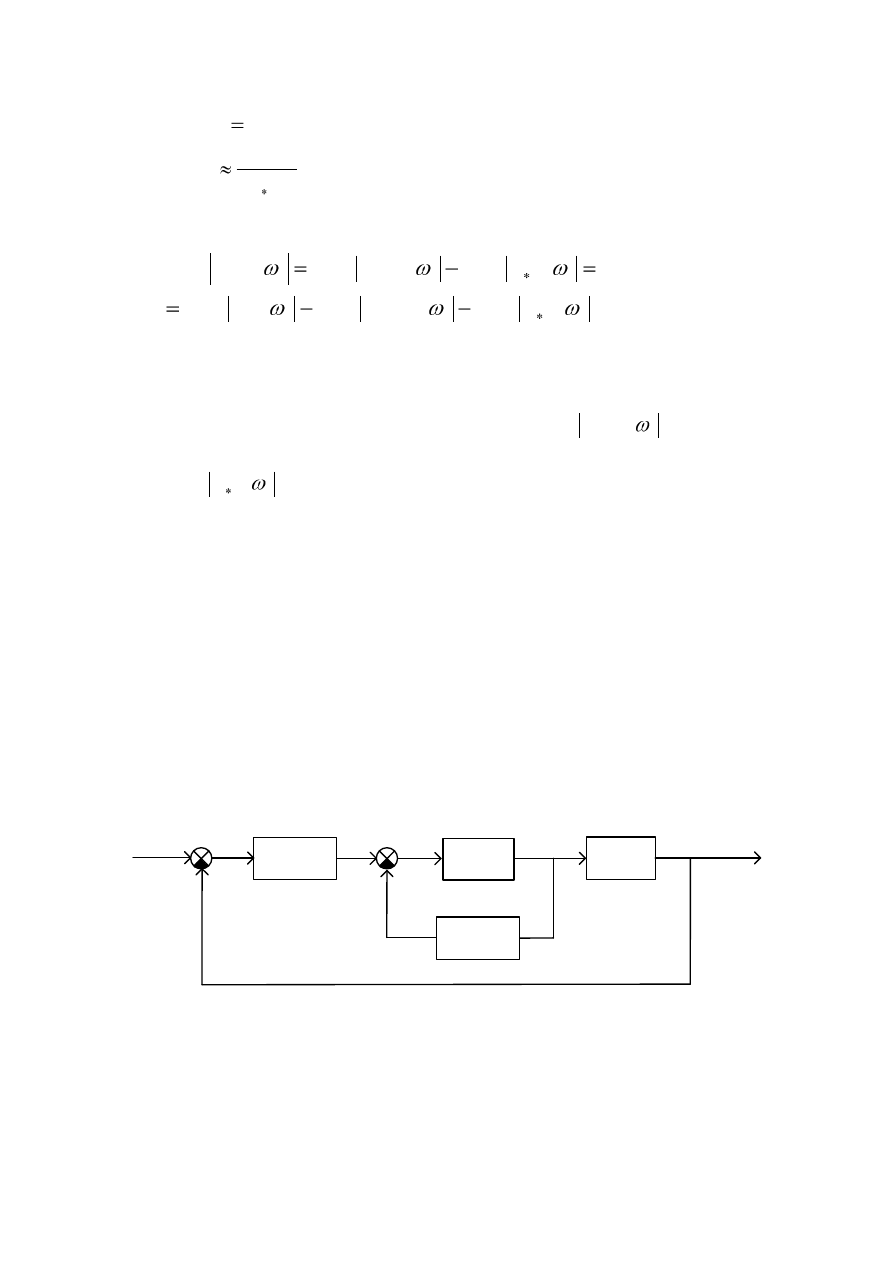
Структурная схема с такими устройствами приведена на рис. 12.
W
1ky
(s)
W
2
(s)
W
3
(s)
W
2ky
(s)
)
(s
X
)
(t
x
)
(s
Y
)
(t
y
Рис. 12. Структурная схема САУ с последовательным и параллельным
корректирующими звеньями.
Передаточная функция скорректированной разомкнутой системы, которая
является желаемой, будет иметь вид

26
)
(
)
(
1
)
(
)
(
)
(
)
(
2
НХ
ОХВ
1
s
W
s
W
s
W
s
W
s
W
s
W
ky
ОХВ
ky
.
(37)
Выбор
)
(
1
s
W
ky
и
)
(
2
s
W
ky
будем выполнять для тех диапазонов частот, для
которых справедливо неравенство:
1
)
(
)
(
2
ОХВ
j
W
j
W
ky
.
Тогда зависимость (37) упростится:
)
(
1
)
(
)
(
)
(
2
НХ
1
s
W
s
W
s
W
s
W
ky
ky
(38)
Следовательно,
)
(
lg
20
)
(
lg
20
)
(
lg
20
)
(
lg
20
НХ
2
1ky
j
W
j
W
j
W
j
W
ky
ky
.
На основании полученных выражений для определения последовательного
и параллельного корректирующих звеньев необходимо:
1. Построить по заданным показателям качества желаемой ЛAЧX
разомкнутой системы
)
(
lg
20
j
W
;
2. Построить ЛАЧХ неохваченной части системы
)
(
lg
20
j
W
НХ
;
3. Вычесть из желаемой ЛАЧХ, ЛАЧХ неохваченной системы;
4. Зная, что ЛАЧХ, полученная в результате выполнения операций, является:
)
(
lg
20
)
(
lg
20
2
1ky
j
W
j
W
ky
,задаваясь или
)
(
1
j
W
ky
, или
)
(
2
j
W
ky
, определить
передаточную функцию другого корректирующего звена.
2.7. Построение переходного процесса
Переходный процесс является реакцией САУ
)
(t
y
на единичное входное
воздействие
)
(
1
)
(
t
t
x
при нулевых начальных условиях. Для построения
переходного процесса наибольшее применение нашёл метод трапеций. Метод
трапеций предполагает знание вещественной частотной характеристики
)
(
P
замкнутой системы.
а). Графическое построение переходного процесса для САУ, охваченной
единичной отрицательной обратной связью.
Существует аналитическая связь между передаточной функцией
)
( j
Ф
,
)
( j
W
разомкнутой системы и частотными характеристиками
)
(
P
и
j
V (
):
27
)
(
)
(
)
(
1
)
(
)
(
Ф
j
jV
j
P
j
W
j
W
j
.
(39)
На основе этой связи построены номограммы, представленные на рис.13,
которые позволяют по желаемой ЛАЧХ и соответствующей ей фазовой
характеристике
)
(
определить
)
(
P
. Для этого на номограмме по оси
ординат откладывают значение
)
(
i
L
дБ, а по оси абсцисс -
)
(
i
. В точке
пересечения прямых уровней
)
(
,
)
(
i
i
L
считывается с кривой
номограммы значение
)
(
i
P
для частоты
i
.
Для построения всей характеристики
)
(
P
необходимо взять 10÷15 точек
различных значений желаемой ЛАЧХ и её фазовой характеристики для
i
с
одинаковым интервалом по всему диапазону значимых частот.
При построении переходного процесса
)
(t
y
по вещественной частотной
характеристике
)
(
P
используют следующую методику, представленную на
рис. 14. В этой методике используют так называемый «метод трапеций»:
1. Характеристику
)
(
P
разбивают на трапеции так, чтобы их наклонные
стороны как можно точнее аппроксимировали кривую
)
(
P
;
2. Каждую трапецию вычерчивают на единой оси
с учётом знака площади
рассматриваемой трапеции. Знаки присваивают каждой трапеции так, чтобы
сумма их площадей как можно точнее аппроксимировала площадь под кривой
)
(
P
;
3. Для каждой трапеции определяют коэффициент наклона:
j
j
j
2
1
.
4. По таблицам h функций, представленных в [2], для каждой
j
трапеций
выписываем значения стандартных реакций
)
(
j
h
и заполняем табл. 5.
Таблица 5
0,00
0,05
0,10
0,15
… 0,95
1,00
)
(
1
h
…
)
(
2
h
…
…………………………………………………………………
……………………………………………….
)
(
n
h
…