Файл: Математические модели принятия решений - УЧЕБНЫЕ МАТ-2018.docx

Задача математического моделирования процессов при условии достаточно точных наблюдений за входными переменными и выходной переменной формулируется следующим образом:

Найти функцию 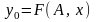и доверительный интервал 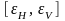для значений 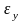. (1.3)

Тогда на практике можно знать ожидаемые значения выходной переменной при известных значениях вектора : .

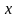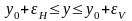Рис. 1.3. Модель процесса в виде «черного ящика».

Обозначения: 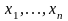– истинные значения вектора входных переменных; 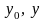– значения детерминированной и случайной составляющих выходной переменной моделируемого процесса; 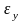– ненаблюдаемые внутренние аддитивные «шумы»; А – вектор параметров.

Математическая модель (1.3) называется эмпирической (ЭМП), если основная информация для ее построения – результаты наблюдений моделируемого процесса или наблюдений за процессами – аналогами моделируемого, и теоретической (ТМП), если существенно используются знания соответствующей теории.

Задание. Рассмотреть примеры построения эмпирических моделей процессов методом наименьших квадратов (МНК) (Задачи приведены в задании к вопросу экзамена 1-3-2 в МОДУЛ).

Справочно: Смотри глоссарий (Приложение 2) пп. 1.2, 1.15, 1.26, 1.27, 1.28.

Тема 1.2. Комплекс моделей годового и стратегического планирования фирмы на основе производственных функций

1.2.1. Производственные функции

Производственная функция (также функция производства) – экономико-математическая количественная зависимость между величинами выпуска (количество продукции) и факторами производства, такими как затраты ресурсов, уровень технологий^¹².

Производственная функция является примером моделей процессов (часто это теоретическая модель процесса производства товаров и/или услуг). Рассматривается годовое количество произведенной фирмой продукции в стоимостной или натуральной форме. Факторами производства выступают объемы потребленных фирмой ресурсов (в стоимостном или в натуральном измерении). Главными ресурсами выступают потребленные за год количества труда и капитала^¹³.

Определение. Функция 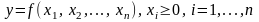называется производственной, если выполнены следующие ее свойства:

1. Нулевой выпуск в отсутствии одного или нескольких ресурсов.

2. Неотрицательная производительность факторов .

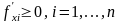3. Убывающая эффективность факторов .

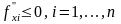4. Линейная однородность или постоянная отдача от масштаба .

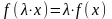Примеры производственных функций:

1. Классическая производственная функция Кобба-Дугласа (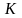 – амортизация капитала фирмы, 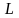– фонд заработной платы за рассматриваемый период времени):

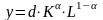, (1.4)

где 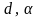– параметры функции, индивидуальные для фирмы ( ).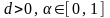

2. Обобщенная функция Кобба-Дугласа:

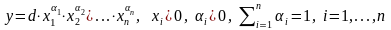. (1.5)

3. Линейная производственная функция:

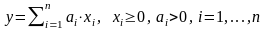. (1.6)

4. Производственная функция с нулевой эластичностью замещения ресурсов:

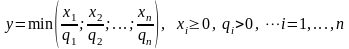. (1.7)

Задание 1 к вопросу 1.2.1. В записанных функциях (1.4) – (1.7) укажите аргументы и параметры, поясните их экономический смысл и размерности.

Задание 2 к вопросу 1.2.1. Покажите, что функции (1.4) – (1.7) удовлетворяют определению производственных функций.

Справочно: Смотри глоссарий (Приложение 2) пп. 1.9, 1.16, 1.19, 1.24.

1.2.2. Задача оптимального среднесрочного плана развития производства

С использованием производственной функции рассмотрим задачу выбора оптимального соотношения запасов ресурсов. Эту задачу можно интерпретировать как задачу среднесрочного планирования развития фирмы.

Пусть для некоторой фирмы известна производственная функция, ее товарная, ресурсная и технологическая политика стабильна, а спрос на продукцию неограничен. Пусть также в среднесрочной перспективе заданы границы интервалов 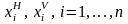возможного изменения каждого из существенных производственных ресурсов: 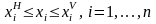. Тогда можно найти оптимальные значения ресурсного обеспечения производства решение следующей задачи. Найти 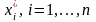из условий:

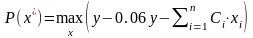; (1.8)

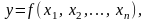
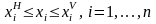. (1.9)

В задаче (1.8) – (1.9) 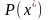– оптимальная годовая прибыль производственной деятельности фирмы с учетом налога, равного 6% от выручки; 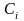– цена ресурса i (для ресурсов производства, учитываемых в стоимостном измерении, их цена принимается равной единице).

Можно показать (с учетом свойств производственной функции), что задача (1.8) – (1.9) относится к классу задач выпуклого программирования и ее решение можно получить в среде Excel.

1.2.3. Методы исполнения решений на различных этапах цикла принятия решений на примере задачи распределения ресурсов

На практике Центры принятия и реализации решений не являются идеально организованными и хорошо информированными. Тогда ожидаемые результаты не совпадают с реальными, особенно в ситуациях при больших по времени периодов реализации решений. Возникает необходимость совершенствования методических, математических и инструментальных методов принятия и реализации решений.

Выделим следующие этапы цикла принятия и реализации решений:

1. Сбор исходных данных и анализ экономической проблемы.

2. Обоснование оптимального решения и его принятие.

3. Реализация решения.

4. Оценка полученного результата и при необходимости внесение изменений в регламентные процедуры.

Характерным примером для данной темы является проблема распределения ограниченного ресурса. Она возникает в бюджетной сфере государственного и муниципального управления, производственных системах (корпорациях), при организации коллективных действий в социологии и политике и др.

Пусть Центр располагает ограниченным ресурсом в объеме 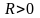и ставит задачу его распределения по 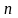исполнителям так, чтобы суммарная эффективность использования ресурса была максимальной. Обозначим 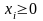объем ресурса, выделяемого исполнителю i (i=1,…,n). Будем считать, что вклад 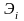исполнителя i в суммарную эффективность зависит от объема выделенного ресурса и определяется выражением: 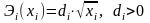, где 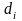– коэффициент, истинное значение которого Центр оценивает с погрешностью.

В предположении, что Центр идеально информирован, найдем оптимальное распределение 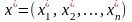решением следующей задачи:

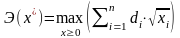; (1.10)

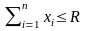. (1.11)

Упражнение. Доказать, что в рассматриваемой формализации задачи при оптимальном решении Центр распределяет весь объем наличного ресурса и балансное ограничение (1.11) выполняется как равенство:

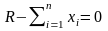
Решение задачи (1.10) – (1.11) найдем с использованием метода множителей Лагранжа (см. ссылку: https://ru.wikipedia.org/wiki/Метод_множителей_Лагранжа). Ограничение 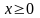пока не рассматриваем. Запишем функцию Лагранжа:

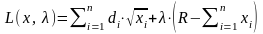. (1.12)

Составим систему из (n+1) уравнений, приравняв к нулю частные производные функции Лагранжа 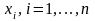по и по : .

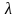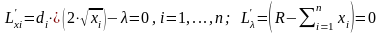Найдем решение первых n уравнений записанной системы в зависимости от :

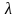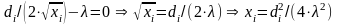. (1.13)

Рассматриваем последнее уравнение системы с учетом выражения (2.13):

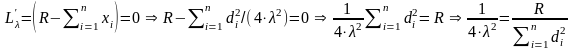. (1.14)

Из выражений (1.13) и (1.14) имеем:

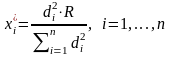. (1.15)

В рассматриваемом случае найденное решение системы (n+1) уравнений удовлетворяет ограничению 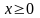и является оптимальным распределением ресурсов в задаче (1.10) – (1.11), поскольку она относится к классу задач выпуклого программирования.

Рассмотрим порядок использования полученных расчетов на практике контроля процессов принятия и реализации решений, которое можно провести только после завершения цикла (после полной или частичной реализации решения). Для этого предлагается использовать расчетные и фактические значения эффективностей распределения и использования ресурсов. Профессиональное расследование эффективностей проводится с использованием методов экономической безопасности.

Оптимальное распределение ресурса согласно (1.15) зависит от коэффициента 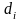: 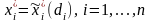. Если при распределении ресурсов (не важна причина) использовались оценки 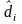(в общем случае 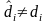) то рассчитанные с использованием выражения (1.15), уровни эффективности 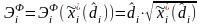отличаются от истинных значений (которые аналитику следует восстановить). Согласно этапу п.4 цикла принятия и реализации решений необходимо внести изменения в соответствующие регламенты, учитывая возможные причины отклонений: либо искажение информации, либо ошибки формализации проблемной ситуации, либо погрешности вычислений, либо объективное изменение условий принятия и реализации решений.

Справочно: Смотри глоссарий (Приложение 2) п. 1.29.

Тема 1.3. Математические модели поддержки принятия решений в условиях риска и неопределенности.

1.3.1. Принципы обоснования решений в условиях риска и неопределенности.

Рассматриваем методы обоснования оптимальных решений с использованием математической модели (1.2). Если относительно значений параметра w информация ЛПР будет полной к моменту реализации решений (но не к моменту обоснования оптимального решения задачи), то ЛПР может найти решающую функцию :

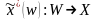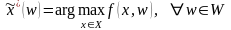. (1.16)

Рассмотрим случай, когда к моменту реализации решений ЛПР не знает вектор параметров w. В литературе рассматриваются два основных подхода к постановке математических задач поиска оптимального решения для модели ЛПР в форме (1.2):

принципы принятия решений при неопределенности, например, принцип гарантированного результата;
принцип осреднения.

Принцип гарантированного результата (критерии Вальда) предполагает выбор 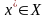решением следующей задачи:

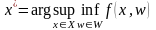. (1.17)

В данном случае ЛПР отыскивает наилучшее решение для наихудших для себя значений w. Заметим, что справедлива оценка

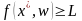, где .

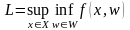Другие подходы к обоснованию оптимальных решений в условиях неопределенности представлены в методических материалах индивидуальных заданий.

Рассмотрим принцип осреднения, т.е. обоснование решений при риске. Предположим, что в (1.2) w подчиняется распределению с известной плотностью 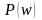, тогда принцип осреднения предлагает выбор 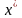с использованием следующей целевой функции:

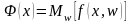, (1.18)

где M_w – оператор математического ожидания.

Далее задача нахождения 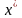сводится к (1.1) с целевой функцией (1.18).

Упражнение. Рассмотреть принципы обоснования решений Байеса-Лапласа, Сэвиджа, Гурвица для непрерывной модели и записать математические задачи поиска оптимальных решений, аналогичные задаче (1.17).

Справочно: Смотри глоссарий (Приложение 2) п. 2.4.

1.3.2. Портфельный анализ: модель Марковица.

Портфельная теория Марковица (англ. mean-variance analysis) – подход, основанный на анализе ожидаемых средних значений и вариаций случайных величин) – разработанная Гарри Марковицем методика формирования инвестиционного портфеля, направленная на оптимальный выбор совокупности активов, исходя из требуемого соотношения доходность/риск. Сформулированные им в 1950-х годах идеи составляют основу современной портфельной теории^¹⁴.

Можно рассмотреть два различных подхода к формированию портфеля.

Первый связан с выбором активов, доходность которых стабильна, но существует не нулевая вероятность потери активов. Тогда цель портфельного анализа состоит в определении оптимального набора активов, при котором риски потерь являются минимальными. Данная стратегия портфельного анализа выражена рекомендацией: «не храните яйца (деньги) в одной корзине (в одном банке, одном активе)».

Второй подход, для которого применима теория Марковица, состоит в выборе совокупности компенсационных активов. Считается, что доходность активов является случайной величиной, но вероятности их полных потерь нулевые. Тогда цель портфельного анализа состоит в выборе совокупности активов, которая обеспечит высокую среднюю доходность (критерий 1) и минимальное отклонение уровня дохода от этого среднего (критерий 2 – риск должен быть минимальным). Снижение риска достигается использованием компенсационных активов, коэффициент корреляции доходностей которых является отрицательным. Модель Марковица позволяет выбрать оптимальный набор компенсационных активов с высокой средней доходностью.

При записи модели используются свойства математического ожидания и формула математического ожидания суммы случайных величин. Пусть для формирования оптимального портфеля выбраны n активов, доходность которых на период инвестирования – случайные величины 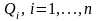с математическими ожиданиями 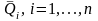и дисперсиями 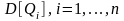. Пусть 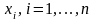– доли использования каждого актива в формируемом портфеле, которые удовлетворяют условиям:

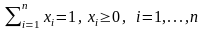. (1.19)

Тогда доходность портфеля 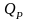на периоде инвестирования – случайная величина, которая зависит от доходности активов и определяется по следующей формуле:

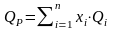. (1.20)

Найдем математическое ожидание (среднее значение) доходности :

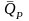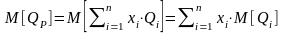Формулу для средней доходности портфеля можно записать в более наглядном виде:

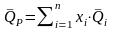. (1.21)

Из формулы (1.21) следует, что средняя доходность формируемого портфеля определяется средними доходностями активов и долями их включения в портфель.

Найдем выражение для дисперсии доходности портфеля :

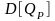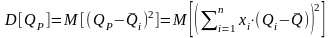Откуда получаем формулу для дисперсии портфеля в матричной записи:

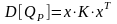. (1.22)

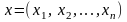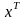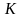Здесь вектор – доли активов размерностью (1 × n); – вектор столбец долей активов размерностью (n × 1); – ковариационная матрица активов, которая отражает взаимозависимость доходностей выбранных активов, размерностью (n × n).