Файл: ЛР Специальные главы математики.pdf

21 

1) Запустить программу Excel. Создать документ Книга1. Сохранить в 

отведенное место на жестком диске под оригинальным именем, например, Книга 

Иванова. Первая лабораторная работа выполняется на листе Лист1 вашей первой 

электронной книги, переименовать его в Лаб1. 

2) Создать заголовок сверху по центру будущей таблицы, используя шрифты 

помельче, 12 пунктов, Аrial курсив и покрупнее, 14 пунктов, Times Roman 

полужирный. Выделить название темы лабораторной цветом. 

3) Сделать подпись Выполнил, Дата, Вариант. Дата должна показывать 

текущую дату в заданном полном формате. Вставить свою функцию по варианту 

в математической нотации как объект MS Equation. Выделить формулу цветной 

рамкой. 

4) Завести отдельные ячейки для начала интервала а

x 

и шага табулирования h

x

, 

ячейки D7 и D8 на рисунке 1.1. Начало интервала определить вручную. Для 

заполнения диапазона ячеек со значениями аргумента функции использовать 

абсолютные адреса этих ячеек. В ячейки C7 и C8 вставьте пояснения Начало 

интервала а

x

 =..  

и Шаг h

x

 =…. 

5) В строке 10 оформить шапку таблицы: Номер точки, Значение аргумента, 

Значение функции, и ниже, в строке 11 сокращенно: №, х, у. 

6) Заполнение таблицы. 

Создание столбца номеров точек. Набрать 1 в В12. Протащить маркер 

заполнения формул с нажатым Ctrl до 79 в всплывающем окне для получения 

арифметической прогрессии с приращением 1 в диапазоне ячеек B13:B90. 

Создание столбца х. В первую сверху ячейку столбца, С12 набираем ссылку на 

начало интервала =$D$7 (абсолютный адрес). Под ней в ячейку C13 формулу для 

расчета следующего значения аргумента через предыдущее =C12+$D$8 

(комбинация абсолютных и относительных адресов). Протаскиваем маркер 

заполнения через диапазон ячеек C14:C90 для получения в нем формул расчета 

значений аргумента. 

Создание столбца y. В ячейку D12 набираем формулу расчета функции по 

варианту для первой строки таблицы. Для 0-го варианта =sin(3*C12)^2-
log10(C12-

2) (относительный адрес х). Далее используем технику протаскивания 

формулы для заполнения диапазона ячеек D13:D90 со значениями функции. 

7) Форматирование таблицы. Вывести 5 значащих цифр для значений х и 10 

для у. 

Выровнять по десятичной точке. Назначить холодный цвет, например, синий, 

отрицательным значениям и красный положительным. Навести рамки в 

таблице по образцу на рисунке 1.1. 

8) Посчитать значения функции для х=0.0 и х=1.0.  

9) Посчитать максимальное Y

max

и минимальное Y

min

значения функции в 

полученном диапазоне ячеек. 
1) 

График функции в Excel, как и все остальные диаграммы, строится по 

дискретным значениям. Исходные данные для графика получены в предыдущей 

лабораторной работе. 

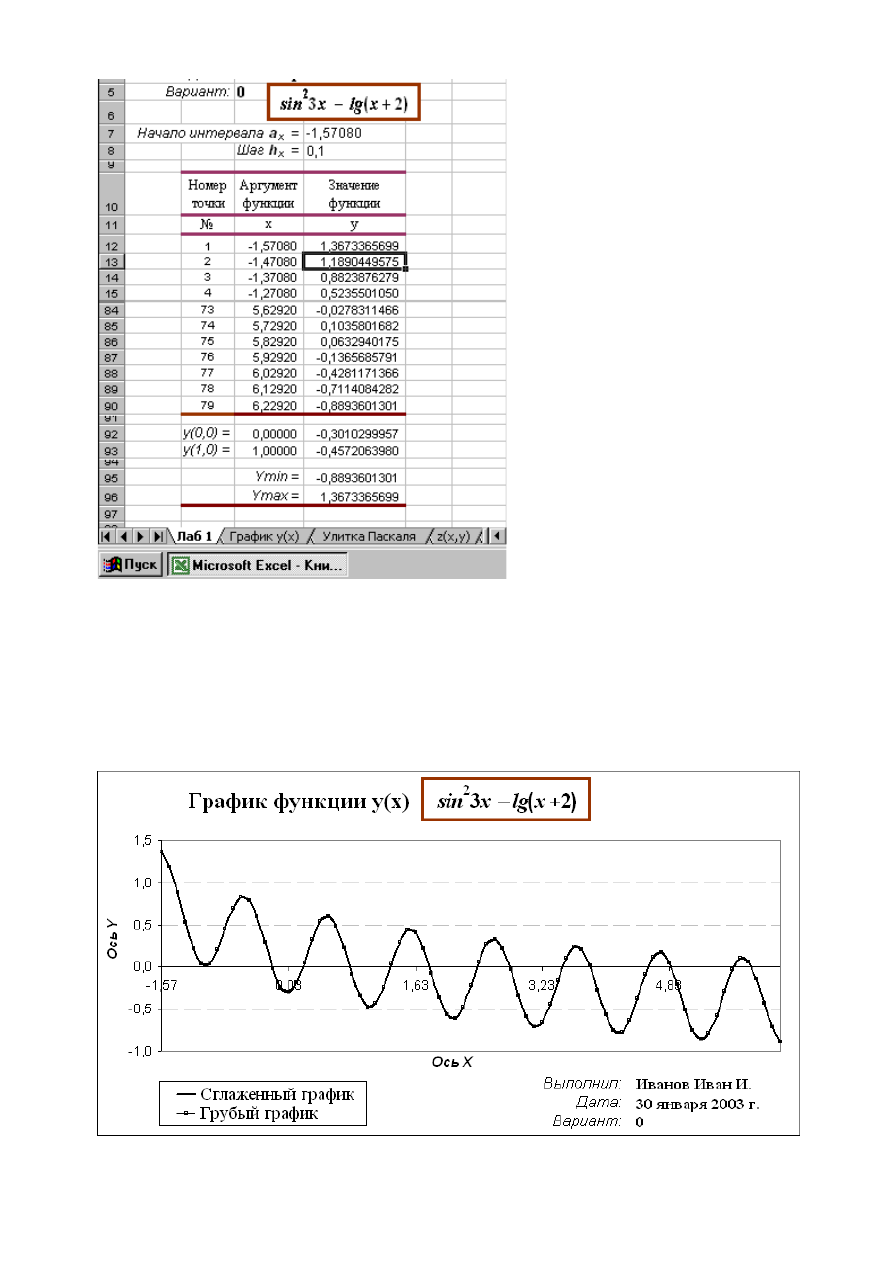
22 

Рисунок 1.1. Образец оформления лабораторной работы 

2) Запускаем Мастера диаграмм. Выбираем тип диаграммы График. Во втором 

окне мастера указываем исходные данные для первого ряда Значения: столбец y, 

Подписи оси Х: 

столбец  x, Имя: набираем с клавиатуры Грубый график. Для второго ряда 

Значения и Подписи по оси Х те же, Имя: Сглаженный график. Лишние ряды 

удалить. 

2) 

Отформатировать график по образцу рисунка 2.1. 

Рисунок 2.1. Образец оформления графика 

23 

На грубом графике соединить точки отрезками прямых сплошными, тонкими, 

синего цвета, в точках синие прозрачные квадратные маркеры 5 пунктов. На 

глаженном графике -соединяющие точки линии сплошные, толстые, красные, 

сглаженные, без маркеров. 

Настроить порядок рядов так, чтобы тонкие синие линии были видны на фоне 

красных. 

Оформить график заголовком, формулу скопировать на график. Подписать оси 

как Ось Х и Ось Y. Ось Х провести через y=0. Проредить деления шкал, в 

подписях делений отобразить 2-3 цифры, чтобы не загромождали график. 

Настроить диапазон оси Y от Y

min 

до Y

max

своей функции. Подпись Выполнил Дата 

Вариант подставить в шесть надписей из соответствующих ячеек листа. 

Выровнять и распределить надписи инструментами панели Рисование – Действия 
– 

Выровнять, Распределить, Группировка. Убрать серую заливку фона области 

построения. Линии сетки оставить только горизонтальные по основным делениям 

оси Y, уменьшить их яркость до светло-серого цвета. 

1) Работа с книгой. Перенести диаграмму на отдельный лист под именем 

График y(x). Для обзора точности построения ломаной и сглаженной линий 

отобразить график в максимальном масштабе. 

2) Создать новый лист, назвать его «Корень». 

3) Оформить рабочий лист, написав заголовок «Решение уравнения методом 

половинного деления», ниже заголовка добавить надпись «Решить уравнение 

<Ваше уравнение>». 

4) Подготовьте лист для проведения графического отделения корней. Сделайте 

надпись «1. Графическое отделение корней», в ячейку A6 сделайте поясняющую 

надпись «a=», в ячейку A7 – надпись «b=», в ячейку A8 – «Шаг=». 

5) По графику, построенному в листе Графика, определите отрезок, на котором 

находится наименьший положительный корень. Левую границу отрезка укажите 

в ячейке B6, а его правую границу – в ячейке B7. В ячейку B8 занесите формулу 

вычисления шага (b-a)/10. 

6) Протабулируйте функцию y =f (x) на интервале [a, b] с вычисленным шагом 

h. 

Постройте график данной функции. 

7) Сделайте надпись «2. Уточнение отрезка». Подготовьте ячейки для 

занесения величин a, b, h (см. п.3). Запишите значения a и b, определенные с 

помощью графика, величину шага укажите равной 0,1. 

8

) Протабулируйте функцию y =f (x) на новом интервале [a, b] с заданным 

шагом h=0,1. 

9) Сделайте надпись «3. Метод половинного деления». Аналогично тому, как 

это было сделано в пп. 3 и 6, подготовьте ячейки для занесения величин a, b. По 

таблице значений функции y =f (x) определите отрезок, на котором функция 

меняет знак. Это и будет первоначальный отрезок [a, b] для метода половинного 

деления. Скопируйте значения границ этого отрезка в соответствующие ячейки. 

10) Ниже границ отрезка укажите заданное значение точности ε, внесите 

поясняющую надпись «Epsilon=». 

11) Оформите вычисления по методу половинного деления в виде таблицы: 

24 

Установите вывод 7 значащих цифр после десятичной запятой для всех 

значений в столбцах 2-9. 

На первом шаге в ячейках столбцов 2 (значение a) и 3 (значение b) поставьте 

ссылки на ячейки, содержащие границы отрезка после его уточнения (п.8). В 

столбец 3 внесите формулу, соответствующую вычислению c=(a+b)/2, в столбцы 

5, 6 и 7 запишите формулы для вычисления f(a), f(b) и f(c). В столбце 8 вычислите 

длину отрезка [a, b], а в столбец 9 внесите формулу, реализующую условие ЕСЛИ 
b-a

≤2ε, ТО решение=с, ИНАЧЕ решение=” ”. 

На втором шаге вычислений формулы в столбцах 4-9 переносятся 

(“растягиваются”) из первого шага. В столбец 2 вносится формула вида 

ЕСЛИ(f(a)*f(c)<=0;a;c), а в столбец 3 вносится аналогичная формула 

ЕСЛИ(f(a)*f(c)>=0;b;c). 

Здесь вместо f(a), f(c), a, b, c указываются ссылки на соответствующие ячейки. 

Дальнейшие шаги выполняются так же, как второй шаг. 

Копируйте строки таблицы до тех пор, пока в столбце 9 не появится значение 

искомого корня. 

12) Скопируйте полученное значение приближенного решения в отдельную 

ячейку, слева от нее введите надпись «Ответ:», установите вывод 3 значащих 

цифр после запятой. 

Контрольные вопросы и задания 

Варианты функции y(x) к Заданию 1 

Таблица 1 

25