Добавлен: 19.10.2018
Просмотров: 3429
Скачиваний: 9

31
YA= fnf(A / 1): YB = fnf(B / 1)
If YA * YB > 0 Then GoTo 1"xn", "yn"
xn = (A + B) / 2: yn = fnf(xn / 1)xn, ynYA * yn < 0 Then B = xn Else A = xn(B - A)
> E Then GoTo 2.Text = Round(xn, 4).Text = Round(vn, 4)SubSub
Command2_Click()
End Sub
. Для сохранения проекта надо выполнить команду меню File (файл) → Save
Project As
(Сохранить проект как). В диалоговом окне Save File As (Сохранить
файл как) выбрать название диска, на котором должна быть создана папка для
хранения файлов нового проекта. Далее для сохранения формы, следует набрать
имя файла в поле ввода File Name (Имя файла), например Primer1-1, и нажать
клавишу «Enter». Форма Form1 будет сохранена в файле с расширением Primer1-
1.frm.
После сохранения формы следует сохранить проект. В VISUAL BASIC это
происходит автоматически, после чего должно появиться диалоговое окно Save
Project As -
Сохранить проект. Следует набрать то же имя Primer1-2 и нажать
клавишу «Enter». Файл проекта будет сохранен с расширением Primer1-1.vbp.
Теперь запустить проект на выполнение. Выбираем команду Run → Start или
Shift+F
5. В поле Text1 нужно ввести значение A, в поле Text2 - значение B, в
поле Text3 - значение E - после чего нажать кнопку «Старт». В окнах Text4, Text5
появились значения xn, yn. Для завершения работы приложения следует нажать
кнопку «Финиш».
Для решения трансцендентных уравнений в Scilab применяют функцию
fsolve(x0,f),
где х0 - начальное приближение;
f -
функция, описывающая левую часть уравнения f(х) = 0. Последовательно
вызывая функцию fsolve с различными начальными приближениями, получают
все решения заданного уравнения на заданном диапазоне.
Пример. Найти корни уравнения
0
)
1
(
2
5
2
=
−
⋅
−
x
e
x
Этап 1. Отделение корней. С помощью конструкции function ... endfunction
определяется вид функции, задается вектор диапазона значений аргумента х,
вычисляется вектор значений функции у и строится график функции (рис. 11).
Рис. 11. Команды для задания вида функции и построения графика функции
32
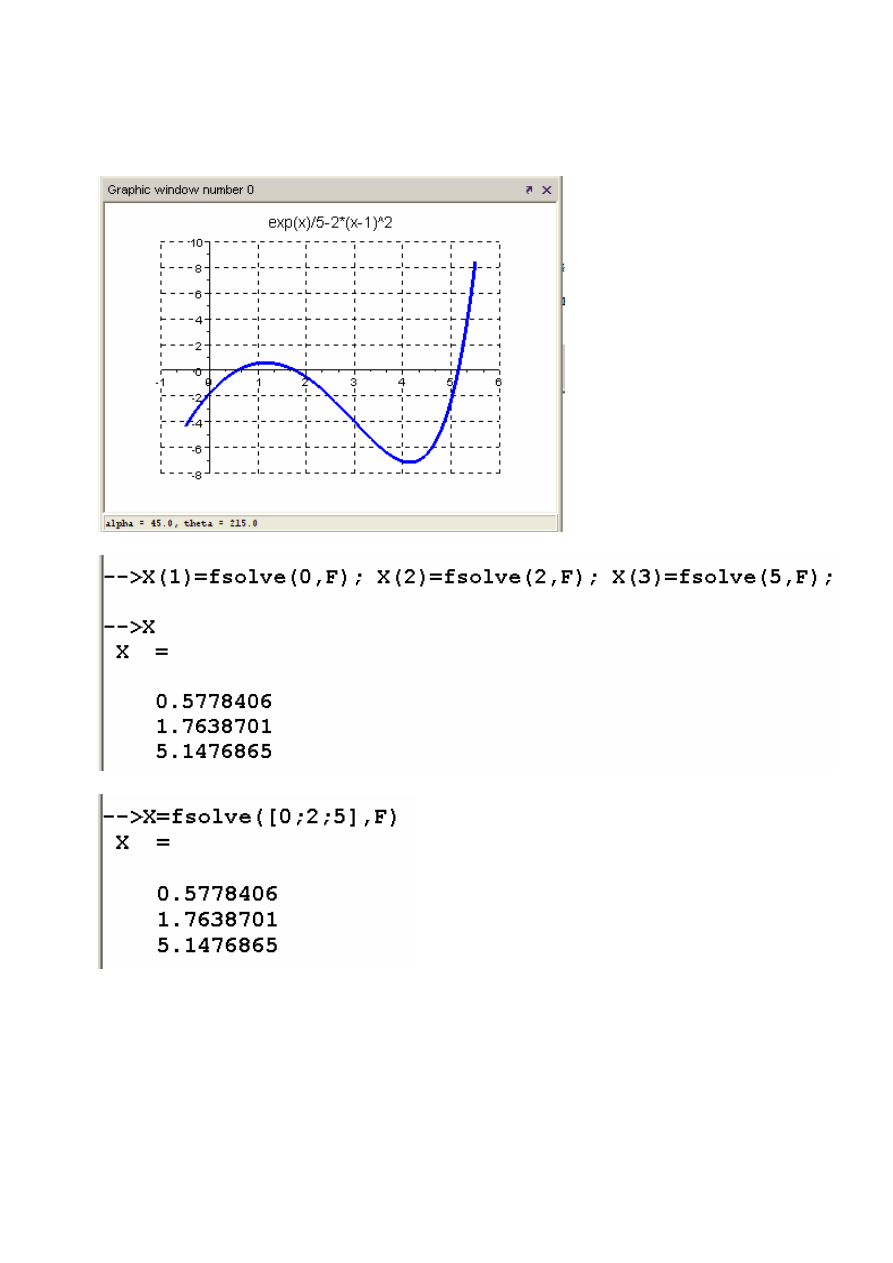
Этап 2. По графику функции (рис. 12) определяются начальные приближения
корней (0, 2, 5). Уточнить корни можно: либо последовательно вызывая функцию
fsolve
с различными начальными приближениями (рис. 13); либо задав вектор
начальных приближений, тогда fsolve вызывается один раз (рис. 14).
Рис. 12. Графическое решение трансцендентного уравнения
Рис. 13. Последовательный вызов fsolve с различным начальным приближением
Рис. 14. Вызов fsolve при задании начальных приближений в виде вектора
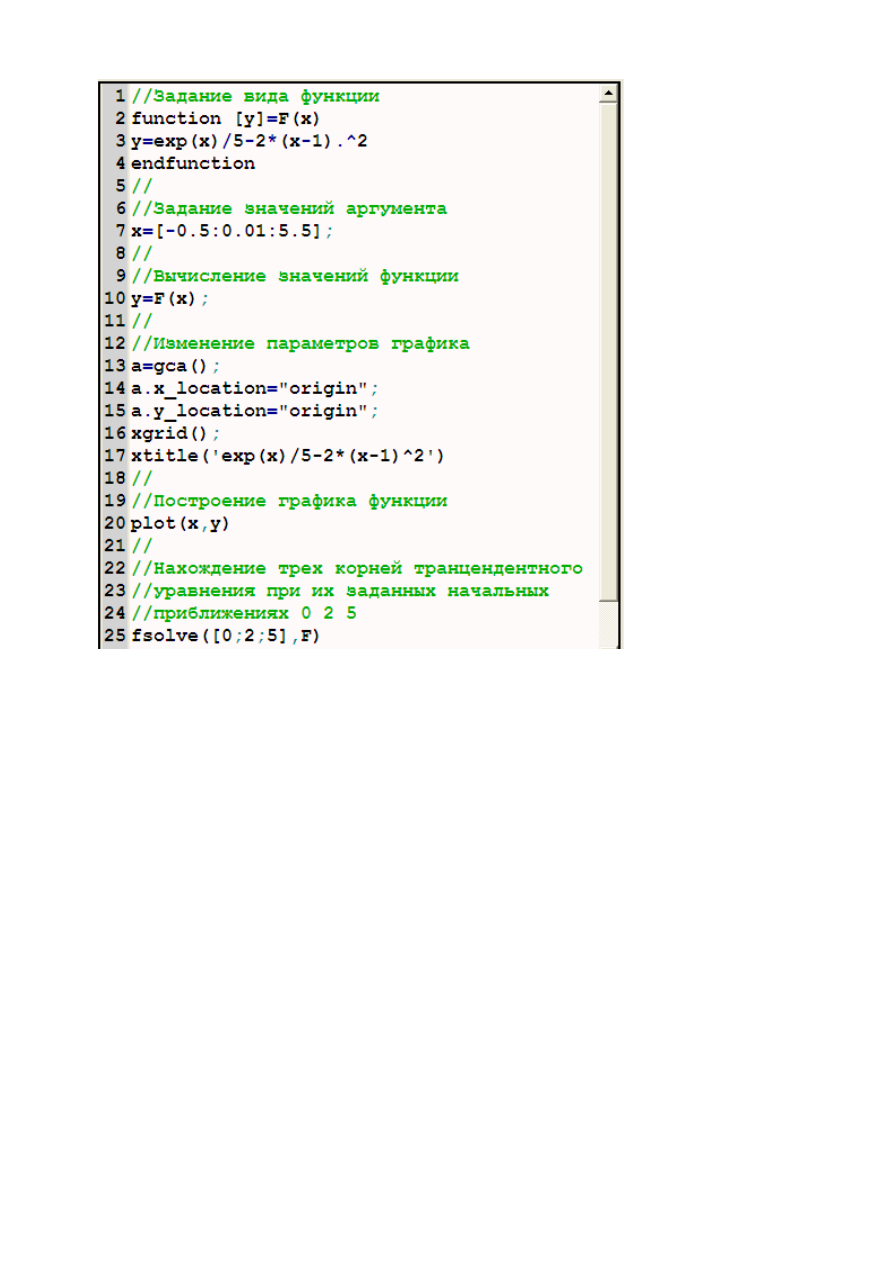
На рис. 15 приведен файл-сценарий нахождения корней трансцендентного
уравнения.
33
Рис. 15. Файл-сценарий построения графика трансцендентного уравнения
и нахождения его корней
Контрольные вопросы.
1)
Какие точные методы решения нелинейных уравнений вы знаете?
2)
Для чего нужен первый этап - отделение корней?
3)
Сформулируйте условия существования решения уравнения. Являются ли
эти требования необходимыми и достаточными?
4)
Что можно сказать о точности методов половинного деления, хорд,
касательных и комбинированного? По каким параметрам их еще можно
сравнить?
Лабораторная работа №2
Тема: Численные методы решения систем линейных уравнений.
1.
Цель работы
Использование методов решения систем линейных уравнений для решения
конкретных научных задач.
2.
Учебные вопросы, подлежащие рассмотрению:
−
Метод простой итерации
−
Оценка погрешности решения системы линейных алгебраических
уравнений.
−
Понятие об обусловленности. Метод прогонки, трехдиагональная матрица.

34
−
Релаксация.
3.
Порядок выполнения работы
Задание
Дана система трех линейных уравнений с тремя неизвестными:
=
+
+
=
+
+
=
+
+
3
3
33
2
32
1
31
2
3
23
2
22
1
21
1
3
13
2
12
1
11
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
1. Решите систему методом Гаусса:
а) используя «ручную» схему единственного деления, двумя способами: без
перестановки строк; с перестановкой строк; расчеты выполняйте с тремя знаками
после запятой (с применением калькулятора); подставьте найденные решения в
исходную систему, вычислите невязки и сравните полученные решения; выбрав
ведущие элементы схемы единственного деления, найдите значение
определителя системы;
б) с помощью программы для ЭВМ с пооперационным учетом ошибок.
2. Решите систему методом простой итерации с точностью ε = 10
-4
с помощью
программы для ЭВМ.
Исполнение: применить а) метод Гаусса; б) метод простой итерации используя
любой инструментальный пакет.
Оценка: Сопоставление полученных результатов, решаемых различными
методами.
Методические указания
В табличном процессоре Excel для решения систем уравнений есть два
варианта: реализация алгоритмов в электронной таблице с помощью основных
средств табличного процессора и использование специальных средств.
Первый вариант проиллюстрирован на примере системы уравнений
−
=
+
−
+
−
=
+
+
−
=
+
−
+
=
+
+
13
9
3
7
3
3
5
3
1
5
4
2
5
2
2
4
3
2
1
4
2
1
4
3
2
1
4
2
1
x
x
x
x
x
x
x
x
x
x
x
x
x
x
На рис. приведены идентичные тексты в Excel, но один — в режиме
отображения формул, а другой — значений. Из них прекрасно видно устройство
алгоритма.

35
Рис.1
Второй вариант не столь очевиден. Среди встроенных в Excel математических
программ программы решения систем уравнений, строго говоря, нет.
Неточно так же, как для решения уравнений было использовано средство
Подбор параметра, для решения систем может быть использовано средство,
предназначенное совсем для другой цели (для решения задач оптимизации).
Это средство - Поиск решения. Поясним его использование и приведем
примеры применения.