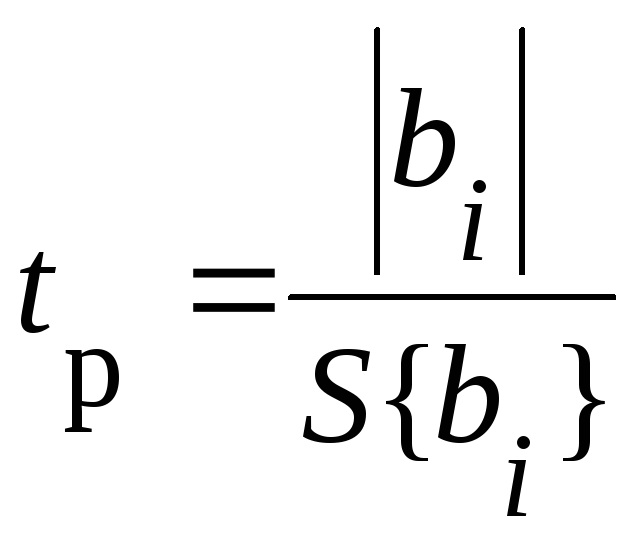ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 176
Скачиваний: 0
СОДЕРЖАНИЕ
Министерство образования и науки
1. Основы теории инженерного эксперимента
1.1. Эксперимент как объект исследования
1.2. Основы теории обработки результатов эксперимента
Анализ и исключение грубых ошибок
Матрицы корреляционных моментов и корреляционных коэффициентов
Вероятностный способ расчета потерь энергии
Полный факторный эксперимент (пфэ)
Дробный факторный эксперимент (дфэ)
Проведение эксперимента и обработка результатов опыта
Проверка адекватности математического описания
Обработка результатов эксперимента при неравномерном дублировании опытов
Обработка результатов экспериментов при отсутствии дублирования опытов
Крутое восхождение по поверхности отклика (метод Бокса-Уилсона)
Экспериментальные планы, рекомендуемые для решения электроэнергетических задач
Для проверки используется Gр - критерий Кохрена, представляющий собой отношение максимальной дисперсии к сумме всех дисперсий:
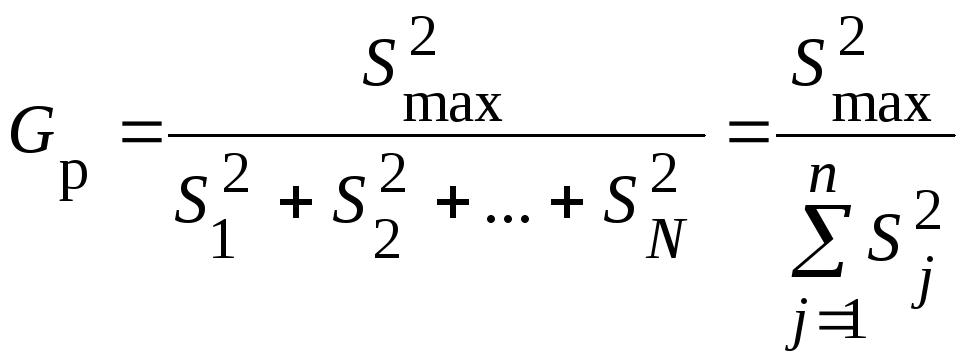 (58)
(58)
Если расчетное
значение Gр
(экспериментальное) Gр<Gкр
(Gкр
- критическое значение при принятом
уровне значимости =0,05
и числе степеней свободы 1=m-1
2=N,
m
- число параллельных опытов, N
- число строк матрицы планирования или
число опытов), то дисперсии однородны.
Если Gр>Gкр
- то дисперсии неоднородны, что указывает
на то, что исследуемая величина не
подчиняется нормальному закону и следует
увеличить число m.
Если дисперсии
![]() опытов однородны, то дисперсию
опытов однородны, то дисперсию![]() воспроизводимости эксперимента
определяют по формуле:
воспроизводимости эксперимента
определяют по формуле:
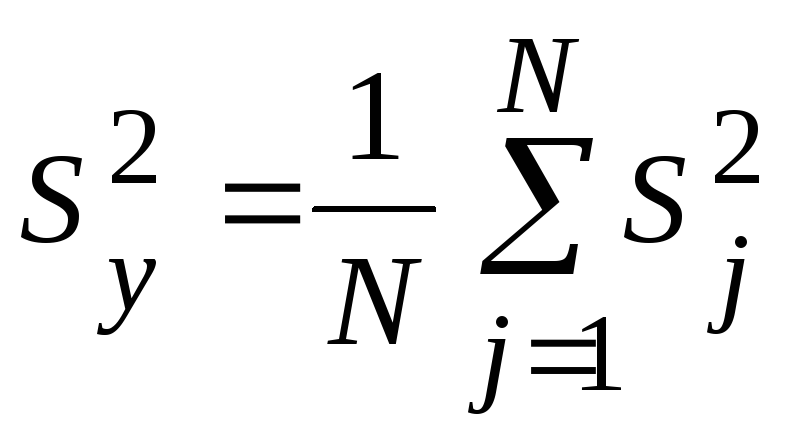 (59)
(59)
По результатам эксперимента вычисляют коэффициенты модели. Свободный член равен:
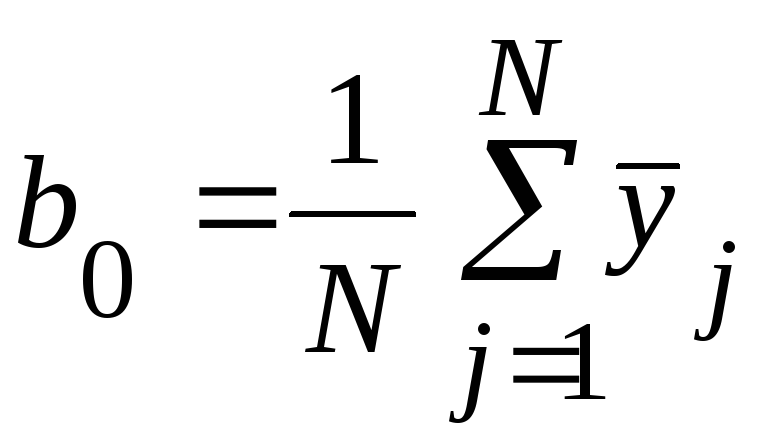 (60)
(60)
Коэффициенты регрессии, характеризующие линейные эффекты определяются по выражению:
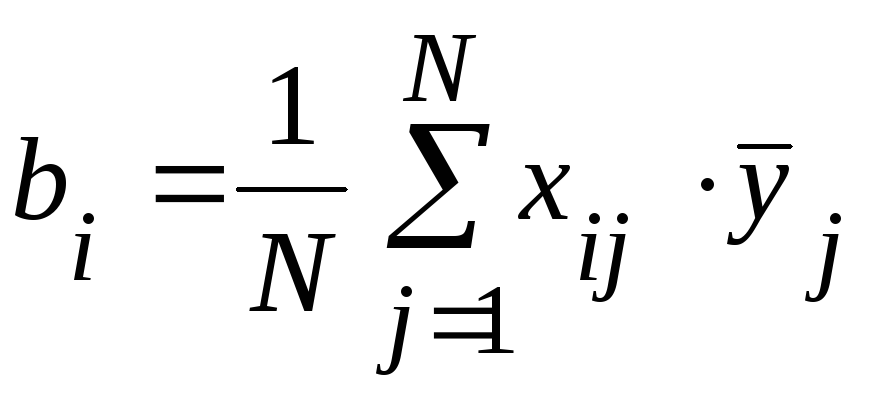 (61)
(61)
Коэффициенты регрессии, характеризующие эффекты взаимодействия равны:
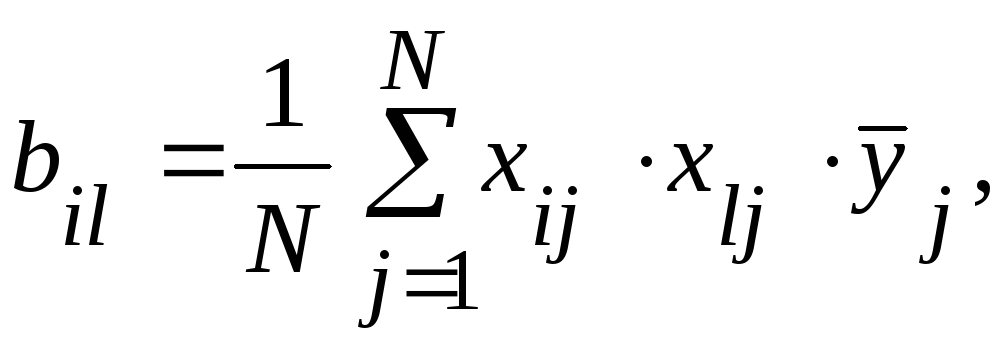 (62)
(62)
где i,
l
- номера факторов; ![]() ,
,
![]() - кодированные значения факторов i
и l
в j-м
опыте.
- кодированные значения факторов i
и l
в j-м
опыте.
Коэффициенты b0,
bi,
bij
- оценки
теоретических коэффициентов 0,
i,
ij
регрессии. Оценки получены по МНК, они
распределены нормально со средними,
равными теоретическими коэффициентами
с
![]()
Проверка значимости коэффициентов проводится по Н0: =0.
1) сравнением абсолютной величины коэффициента с доверительным интервалом;
2) с помощью t-критерия Стьюдента.
По первому способу:
а) вычисляется
дисперсия коэффициентов регрессии
![]() i-го
коэффициента по формуле:
i-го
коэффициента по формуле:
![]() (63)
(63)
б) определяется
доверительный интервал
![]() по выражению:
по выражению:
![]() (64)
(64)
где t
- табличное значение t-критерия
Стьюдента при принятом уровне значимости
и числе степеней свободы ,
с которым определялась дисперсия ![]() ;
f
= (m-1)N;
;
f
= (m-1)N;
![]() - ошибка в определении i-го
коэффициента регрессии.
- ошибка в определении i-го
коэффициента регрессии.
Расчетное значение t-критерия Стьюдента
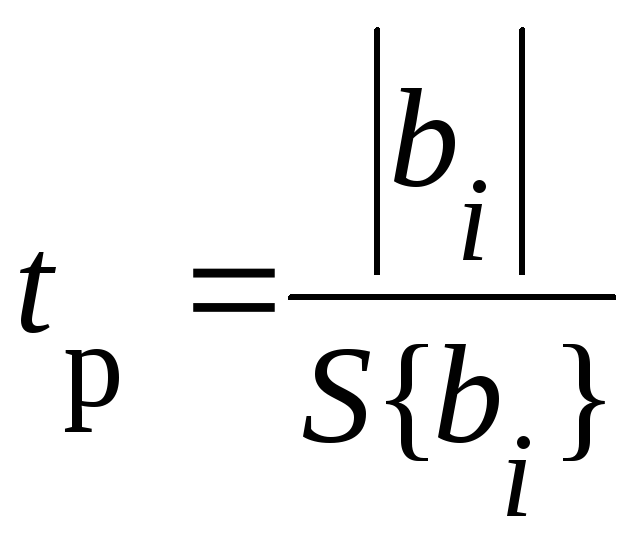 (65)
(65)
сравнивается с
критическим
![]() по таблицам при
и .
по таблицам при
и .
Коэффициент значим,
если
![]() и
и![]() .
Гипотеза Н0
отвергается и оценка коэффициентов
.
Гипотеза Н0
отвергается и оценка коэффициентов
![]() значима. Статистически незначимые
значима. Статистически незначимые![]() могут быть исключены из уравнения.
могут быть исключены из уравнения.
Если
![]() ,
то гипотезу Н0
не отвергают и
,
то гипотезу Н0
не отвергают и
![]() - незначимы. Статистическая незначимость
- незначимы. Статистическая незначимость![]() может объясняться следующим:
может объясняться следующим:
- данный i-й
фактор не имеет функциональной связи
с откликом, т.е.
![]() ;
;
- интервал
варьирования
![]() выбран малым.
выбран малым.
Проверка адекватности математического описания
Гипотеза об
адекватности математического описания
опытным данным проверяется по оценке
отклонения предсказаний по полученному
уравнению регрессии величины отклика
![]() от результатов наблюдений
от результатов наблюдений![]() в одних и тех же точкахg-факторного
пространства.
в одних и тех же точкахg-факторного
пространства.
Рассеяние результатов проводится с помощью дисперсии адекватности:
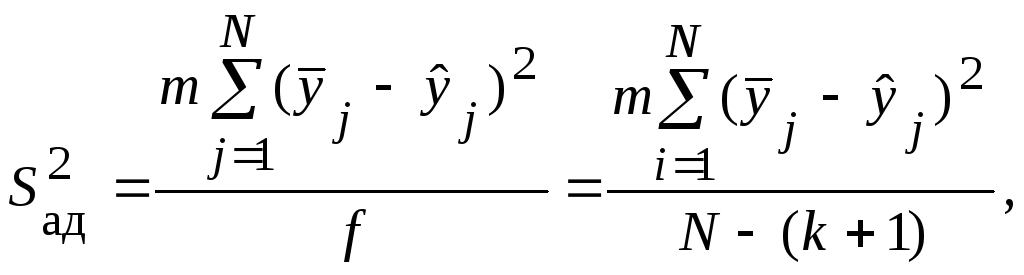 (66)
(66)
где ![]() - среднее значение параметра оптимизации
в j-м
опыте;
- среднее значение параметра оптимизации
в j-м
опыте;
![]() - значение параметра
оптимизации, вычисленное по модели для
условий j-го
опыта;
- значение параметра
оптимизации, вычисленное по модели для
условий j-го
опыта;
f - число степеней свободы: f=N-(k+1);
k - число факторов;
(k+1)=d - число членов аппроксимируемого полинома.
Проверку гипотезы проводят по критерию Фишера:
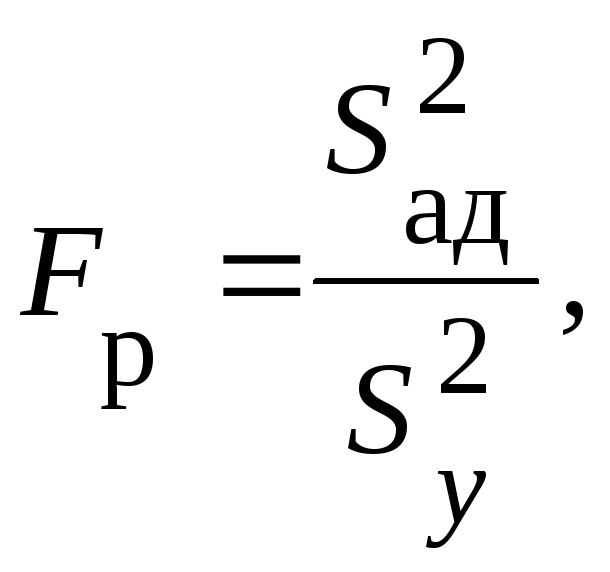 (67)
(67)
где 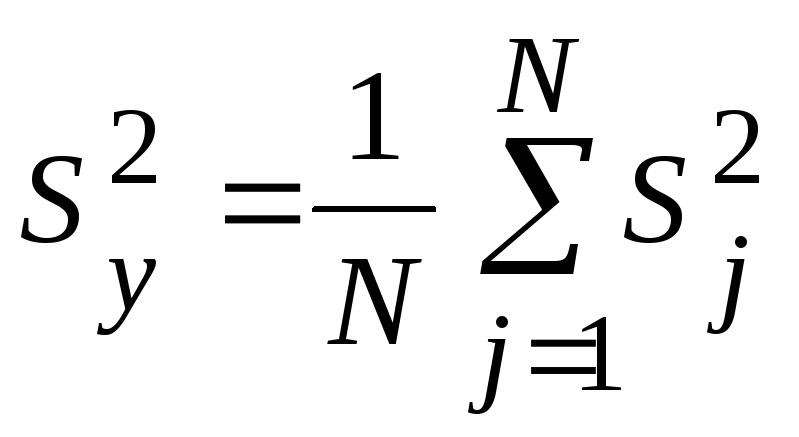 (68)
(68)
Если при заданном
,
![]() ,
,![]() критическое значение
критическое значение
![]() (по таблицам):
(по таблицам):![]() ,
то модель считают адекватной. При
,
то модель считают адекватной. При ![]() - гипотеза об адекватности отвергается,
т.е. гипотеза о соотношении между
- гипотеза об адекватности отвергается,
т.е. гипотеза о соотношении между ![]() и
и ![]() - оценкой дисперсии воспроизводимости
отклика. Проверка адекватности возможна
при
- оценкой дисперсии воспроизводимости
отклика. Проверка адекватности возможна
при ![]() что требует выполнения соотношения
N>d.
что требует выполнения соотношения
N>d.
Обработка результатов эксперимента при неравномерном дублировании опытов
По разного рода
причинам не всегда удается провести
одинаковое число параллельных опытов.
При этом нарушается ортогональность
матрицы планирования и, как следствие,
изменяются формулы для расчета
![]() ,
,![]() и их ошибок. Обработка результатов
экспериментов при неравномерном
дублировании опытов производится по
следующему алгоритму.
и их ошибок. Обработка результатов
экспериментов при неравномерном
дублировании опытов производится по
следующему алгоритму.
1. Для каждой строки матрицы планирования находят среднее значение параметра оптимизации по выражению:
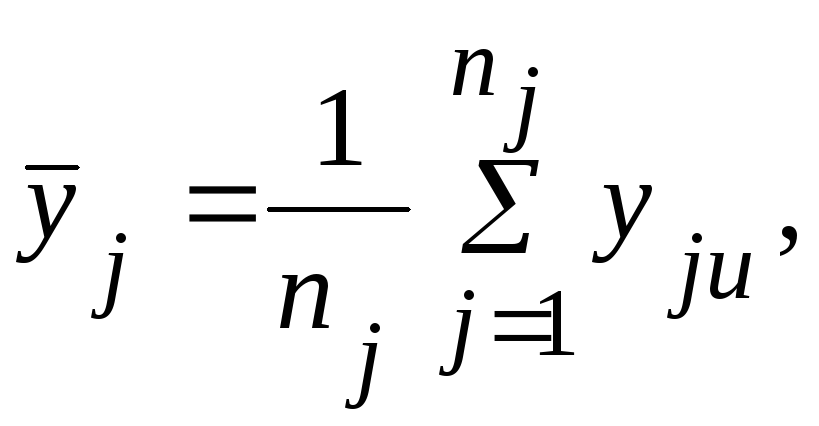
где ![]() - число параллельных опытов в j-й
строке матрицы.
- число параллельных опытов в j-й
строке матрицы.
2. Для каждой строки
матрицы вычисляют дисперсию
![]() опыта:
опыта:
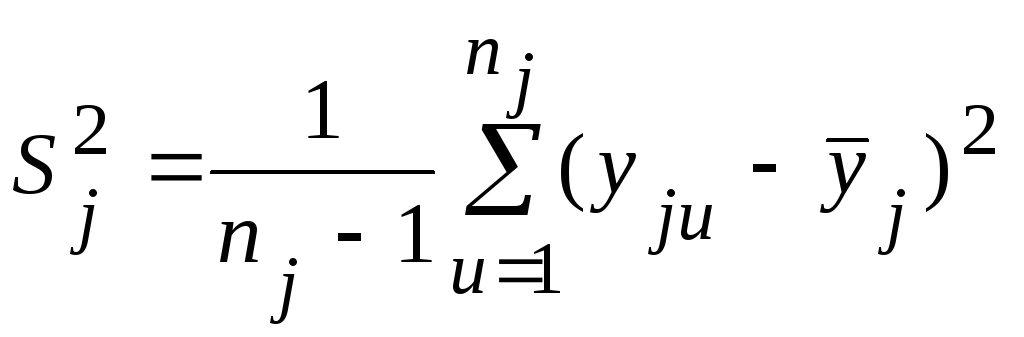 .
.
3. Проверяют с
помощью критерия Бартлета гипотезу
однородности дисперсий опытов. Для
этого подсчитывают дисперсию ![]() воспроизводимости эксперимента по
формуле:
воспроизводимости эксперимента по
формуле:
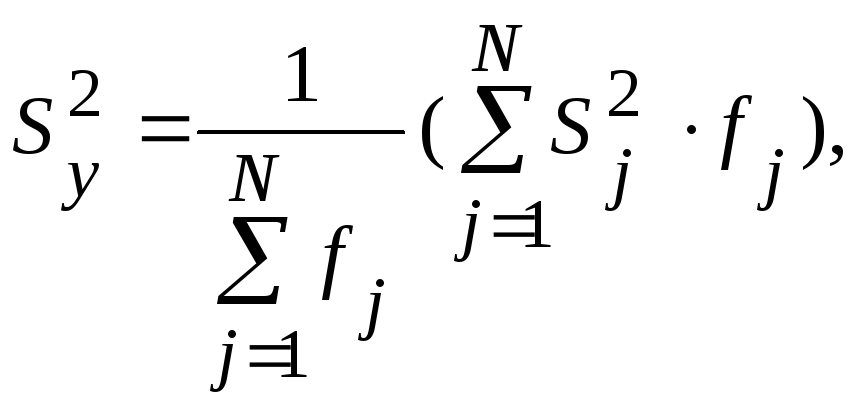
где ![]() - число степеней свободы, с которым
определялась дисперсия
- число степеней свободы, с которым
определялась дисперсия
![]() опыта.
опыта.
Определяют критерий Бартлета по выражению:
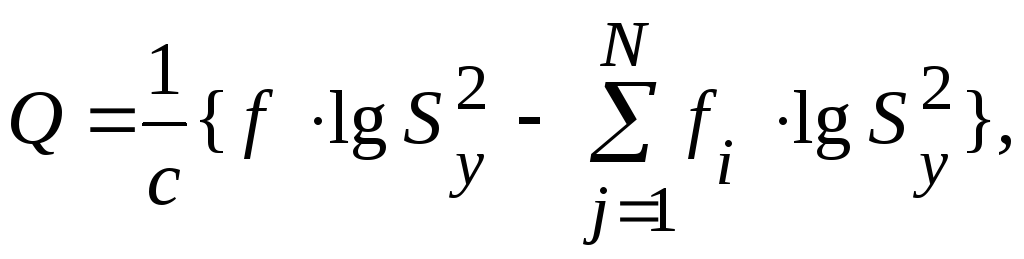
где
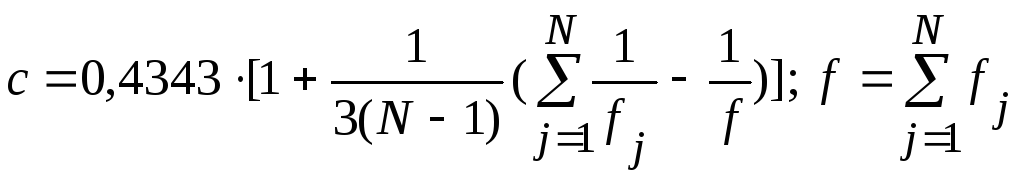 .
.
Критерий Бартлета Q приближенно подчиняется 2 распределению Пирсона с (N-1) степенями свободы, где N - число сравниваемых дисперсий.
Если
![]() (
(![]() - критическое значение 2-Пирсона
для данного числа (N-1)
степеней свободы и принятого уровня
значимости =0,05),
то дисперсии однородны (
- критическое значение 2-Пирсона
для данного числа (N-1)
степеней свободы и принятого уровня
значимости =0,05),
то дисперсии однородны (![]() берется из таблиц).
берется из таблиц).
Критерий Бартлета основан на нормальном законе распределения N: 0,1. Если распределение случайной величины не подчиняется N: 0,1, то проверка однородности дисперсий может привести к ошибочным результатам.
Пример №5.
Матрица планирования
предусматривает постановку 4-х опытов.
Для 1го
опыта n1=5
(повторен пять раз); n2=6;
n3=4;
n4=4.
При этом дисперсии по опытам равны:
![]() Требуется проверить гипотезу об
однородности выборок Н0:
Требуется проверить гипотезу об
однородности выборок Н0:
![]() .
.
Определяем дисперсию
![]() параметра оптимизации:
параметра оптимизации:
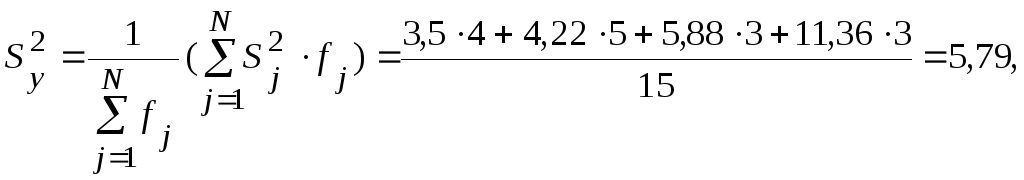
где где ![]() - число степеней свободы, с которым
определялась дисперсия
- число степеней свободы, с которым
определялась дисперсия
![]() j-го
опыта:
j-го
опыта: ![]() ;
;
![]()
Вычисляем величину с:
![]()
Определяем критерий Бартлета:
![]()
Критическое
значение ![]() -Пирсона
при =0,05
для 3х
степеней свободы:
= N-1
= 4-1
= 3, равно:
-Пирсона
при =0,05
для 3х
степеней свободы:
= N-1
= 4-1
= 3, равно: ![]()
Так как
![]() (1,37<7,82), то Н0:
(1,37<7,82), то Н0:
![]() - отвергается, что означает, что
однородность дисперсий обеспечивается.
- отвергается, что означает, что
однородность дисперсий обеспечивается.
4. Вычисляют
коэффициенты
![]() уравнения регрессии, дисперсии
уравнения регрессии, дисперсии![]() коэффициентов регрессии и ошибки -
стандарт
коэффициентов регрессии и ошибки -
стандарт![]() в определении коэффициентов, ковариация
коэффициентов регрессии.
в определении коэффициентов, ковариация
коэффициентов регрессии.
5. Для каждого коэффициента регрессии находят расчетное значение t-критерия Стьюдента по выражению: