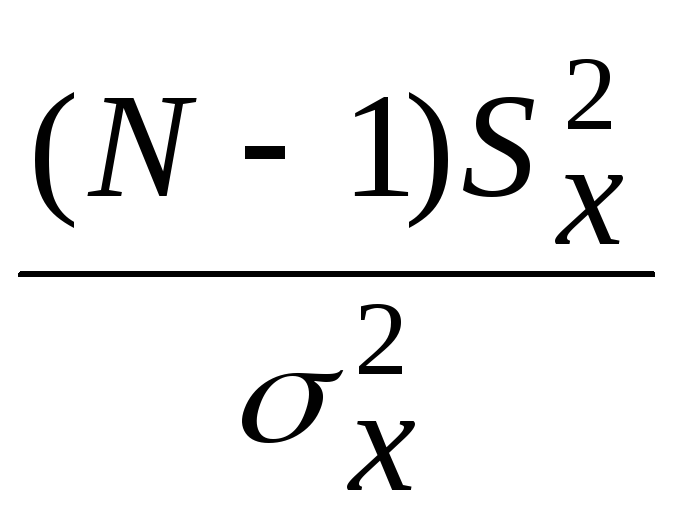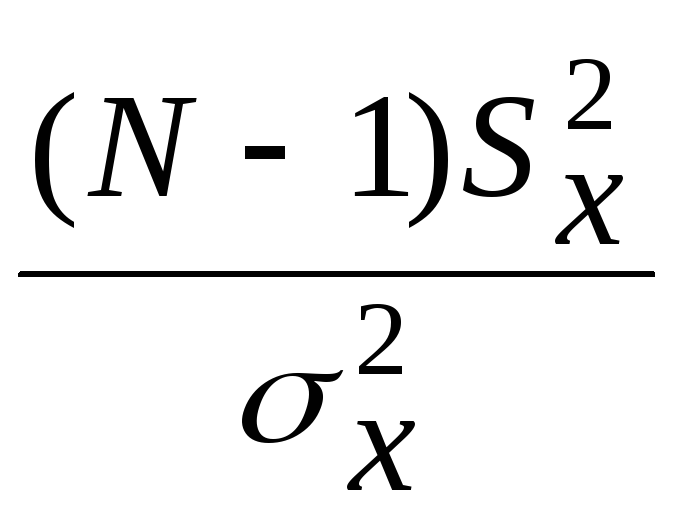ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 160
Скачиваний: 0
СОДЕРЖАНИЕ
Министерство образования и науки
1. Основы теории инженерного эксперимента
1.1. Эксперимент как объект исследования
1.2. Основы теории обработки результатов эксперимента
Анализ и исключение грубых ошибок
Матрицы корреляционных моментов и корреляционных коэффициентов
Вероятностный способ расчета потерь энергии
Полный факторный эксперимент (пфэ)
Дробный факторный эксперимент (дфэ)
Проведение эксперимента и обработка результатов опыта
Проверка адекватности математического описания
Обработка результатов эксперимента при неравномерном дублировании опытов
Обработка результатов экспериментов при отсутствии дублирования опытов
Крутое восхождение по поверхности отклика (метод Бокса-Уилсона)
Экспериментальные планы, рекомендуемые для решения электроэнергетических задач
![]() . (10)
. (10)
Интервал (10)
называется доверительным (ДИ),
![]() ,
,![]() - границы доверительного интервала, р
- доверительная вероятность, а величина:
- границы доверительного интервала, р
- доверительная вероятность, а величина:
![]() (11)
(11)
называется уровнем значимости.
Практически чаще используется р=0,95 (q=0,05) или р=0,9 (q=0,1).
В табл. 1.1 указаны
сведения, необходимые для построения
доверительных интервалов для среднего
значения математического ожидания
![]() ,
когда
,
когда![]() неизвестна, для дисперсии и
среднеквадратического отклонения
неизвестна, для дисперсии и
среднеквадратического отклонения![]() .
Полагается что
.
Полагается что![]() .
Нормальный закон распределения:
.
Нормальный закон распределения:![]() .
.
Таблица 1.1
|
Параметр
|
Информация о параметрах распределения |
Функция
плотности распределения
|
Распределение t(g) |
Формула расчета интервала |
|
|
|
|
t - распределение Стьюдента |
(12) |
|
|
|
|
|
(13) |
|
|
|
|
|
(14) |
![]()
![]() (12)
(12)
![]()
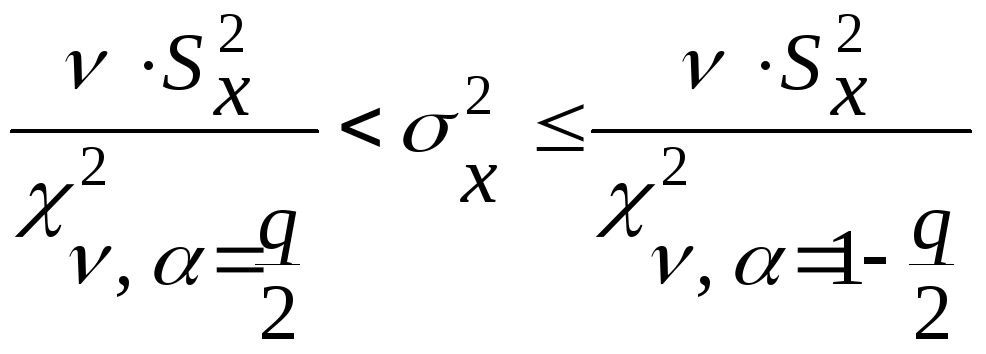 (13)
(13)
![]()
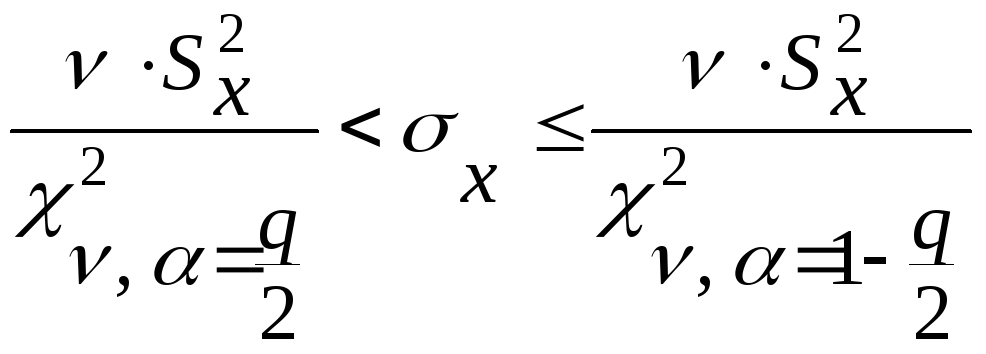 (14)
(14)
В формулах (12-14),
![]() - число степеней свободы,N
- объем выборки,
- число степеней свободы,N
- объем выборки,
![]() ,
гдер
- доверительная вероятность, q
- уровень
значимости,
,
гдер
- доверительная вероятность, q
- уровень
значимости, ![]() - табулированное значение t-критерия
Стьюдента при
- числе степеней свободы и уровне
значимости
- табулированное значение t-критерия
Стьюдента при
- числе степеней свободы и уровне
значимости ![]() ,
,
![]() - табулированное значение
- табулированное значение
![]() -критерия
Пирсона по таблицам.
-критерия
Пирсона по таблицам.
Пример №1.
Пусть по 9 замерам нагрузки на подстанции (N=9) определены точечные оценки (среднее) математического ожидания и дисперсии.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
2 |
3 |
1 |
1,5 |
2,5 |
1,8 |
1,6 |
2,2 |
2,4 |
![]() МВАр,
МВАр,
![]() (МВАр)2,
(МВАр)2,
где
![]() - результат единичного замера нагрузки,
МВАр.
- результат единичного замера нагрузки,
МВАр.
Требуется построить доверительные интервалы:
1) для
![]() прир=0,95
(q=1-p=0,05);
прир=0,95
(q=1-p=0,05);
2) для
![]() прир=0,9
(q=1-p=0,1).
прир=0,9
(q=1-p=0,1).
Число степеней свободы: =N-1=9-1=8.
1) По табулированным
значениям находим ![]() :
:
![]() откуда доверительный
интервал для
откуда доверительный
интервал для
![]() есть (0,0753,925),
т.е.
есть (0,0753,925),
т.е.
![]() ,
,![]() .
По формуле (12):
.
По формуле (12):
![]()
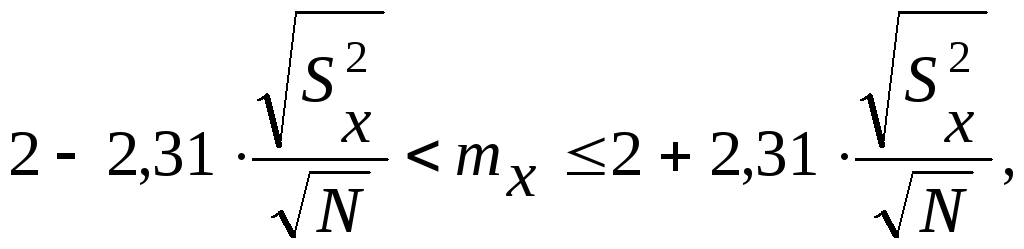
![]()
![]() МВАр.
МВАр.
2) Аналогично по
![]() -таблицам
находим:
-таблицам
находим:
![]()
![]()
![]() :
: ![]()
![]() (МВАр)2.
(МВАр)2.
Анализ и исключение грубых ошибок
Грубые ошибки
должны быть исключены, так как могут
привести к искажению статистических
оценок
![]() и
и![]() .
При этом пользуются проверкой некоторых
статистических гипотез. В качестве
основной (нулевой) гипотезы Н0
рассматривается положение, что все
элементы N-выборки
принадлежат одной генеральной совокупности
с N-распределением.
В качестве альтернативной гипотезы Н1
- что отдельные элементы N-выборки
(
.
При этом пользуются проверкой некоторых
статистических гипотез. В качестве
основной (нулевой) гипотезы Н0
рассматривается положение, что все
элементы N-выборки
принадлежат одной генеральной совокупности
с N-распределением.
В качестве альтернативной гипотезы Н1
- что отдельные элементы N-выборки
(![]() )
имеют:
)
имеют:![]() но
но![]() или
или![]() ,
но
,
но![]() (значения среднего и дисперсии не
совпадают).
(значения среднего и дисперсии не
совпадают).
Для анализа используется t-статистика Стьюдента по правилу Томпсона. Рассчитывается статистика:
![]() (15)
(15)
При принятом уровне
значимости
![]() и числе степеней свободы
и числе степеней свободы![]() по табл.t-критерия
Стьюдента определяется критическое
значение статистики (двусторонний
критерий при
по табл.t-критерия
Стьюдента определяется критическое
значение статистики (двусторонний
критерий при
![]() ).
).
Критерий исключения аномальных наблюдений:
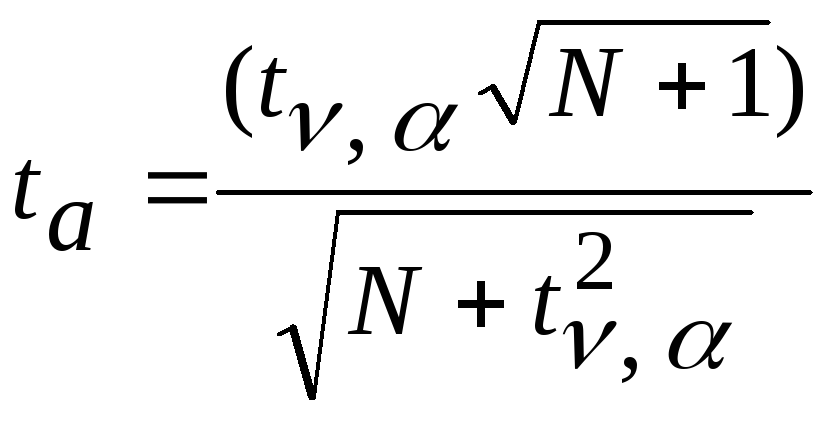 (16)
(16)
Если
![]() ,
то гипотеза Н0
отвергается, если же
,
то гипотеза Н0
отвергается, если же
![]() ,
то гипотеза Н0
принимается.
,
то гипотеза Н0
принимается.
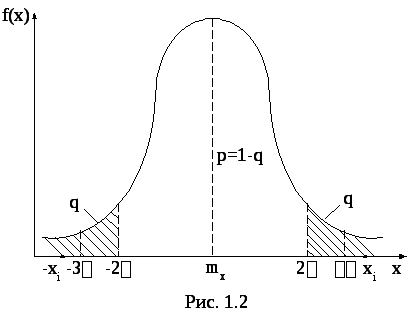
При нормальном
законе распределения можно использовать
критерий «![]() »
или «
»
или «![]() »
- соответственно для уровней значимостиq=0,005
и q=0,05.
»
- соответственно для уровней значимостиq=0,005
и q=0,05.
Тогда если
![]() ,
то
,
то![]() из выборки исключается, как грубая
ошибка (рис. 1.2).
из выборки исключается, как грубая
ошибка (рис. 1.2).
Другой алгоритм проверки:
Н0:
![]() Н1:
Н1:
![]()
Из проведения 10
опытов (N=10)
получено:
![]()
По формуле 8 (![]() )
определяем
статистику:
)
определяем
статистику:
![]()
![]()
![]()
Так как
![]() ,
то гипотеза Н0
отвергается.
,
то гипотеза Н0
отвергается.
Матрицы корреляционных моментов и корреляционных коэффициентов
Две случайные величины х и у называются независимыми, если:
![]() (17)
(17)
Как и в одномерном
случае, основные свойства двумерной
совокупности величин х
и у,
могут быть охарактеризованы рядом
числовых параметров:
![]() .
Кроме них для двумерной совокупности,
простейшими параметрами, характеризующими
степень взаимозависимости переменныхх
и у,
являются ковариация или корреляционный
момент двух случайных величин:
.
Кроме них для двумерной совокупности,
простейшими параметрами, характеризующими
степень взаимозависимости переменныхх
и у,
являются ковариация или корреляционный
момент двух случайных величин:
![]() (18)
(18)
Для определения взаимных корреляционных моментов дискретных случайных величин х, у по множеству значений величин xi (i=1R1), yj (j=1R2), получаем формулу:
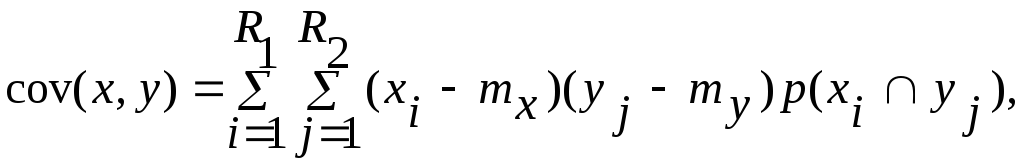 (19)
(19)
где под вероятностью
![]() понимается общая вероятность тех точек
вероятностного пространства, для которых
выполняются соотношения
понимается общая вероятность тех точек
вероятностного пространства, для которых
выполняются соотношения
![]() .
.
Для независимых
случайных величин х,
у
совместная вероятность ![]() равна произведению индивидуальных
вероятностей:
равна произведению индивидуальных
вероятностей:
![]() при этом
при этом![]() .
.