Файл: лекции по планирован.эксперименту.doc

Если заменить произведение х₁х₂=х₃, то матрица полуреплики ДФЭ N=2^3-1 будет иметь вид (табл. 1.5).

Таблица 1.5

В табл. 1.4 для ПФЭ 2² (произведение х₁х₃ и х₂х₃, где х₃= х₁х₂) совпадают столбцы с элементами столбца х₂ и х₁ соответственно, т.е. Коэффициентявляется оценкой влияния факторах₁ и парного взаимодействия х₂х₃ на y_i - функцию отклика. Оценки, в которых невозможно разделить линейный эффект и эффект взаимодействия, называются смешанными. Желательно смешивать с. Число несмешанных линейных эффектовв дробной реплике называется ее разрешающей способностью. Так как прямая оценка разрешающей способности () затруднена, то обычно дробные реплики задают с помощью генерирующих соотношений, показывающие какое из взаимодействий принято незначимым и заменено новым фактором.

План типа 2^3-1 может быть представлен двумя полурепликами, которые задаются одним из следующих генерирующих соотношений:

. (52)

Генерирующие соотношения умножим на новую независимую переменную х₃:

(53)

Две полуреплики 2^3-1 приведены в табл. 1.6.

Таблица 1.6

Поскольку то получим:

(54)

В результате умножения генерирующего соотношения на новую переменную получают определяющий контраст (54). Зная его, можно найти соотношения, задающие совместные оценки. Для этого необходимо умножить независимые переменные х₁, х₂, х₃ на определяющий контраст. Для х₁ получим: . Так как то получим:.

Для х₂ и х₃, после умножения на определяющий контраст, получим:

.

Это означает, что коэффициенты регрессии будут оценками:

Расчет ведется по одной полуреплике (например ), если возникает сомнение, чтото можно поставить еще 4 опыта по полуреплике (), тогда получаем ПФЭ 2³.

В дробных репликах используется часть ПФЭ, которая делится таким образом, чтобы разность между числом оцениваемых параметров (k) и числом опытов (N) была бы минимальна, что обеспечивает наибольшую эффективность (N>k, min N=k+1 - для проверки гипотезы об адекватности модели).

Для модели 2² имеем: ,k=N (4 опыта=) - нет степеней свободы. Если принять, что взаимодействие, тогда выполняется условиеN>k, N=k+1, 4=3+1.

Свойства матриц пфэ и дфэ

1. Симметричность относительно центра эксперимента - алгебраическая сумма элементов столбца каждого фактора равна нулю:

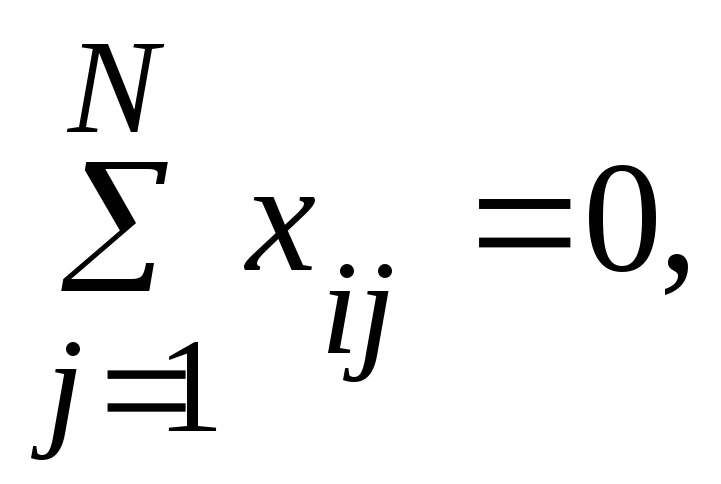
где j - номер опыта; i - номер фактора; N - число опытов.

2. Свойство нормировки - сумма квадратов элементов каждого столбца равна числу опытов:

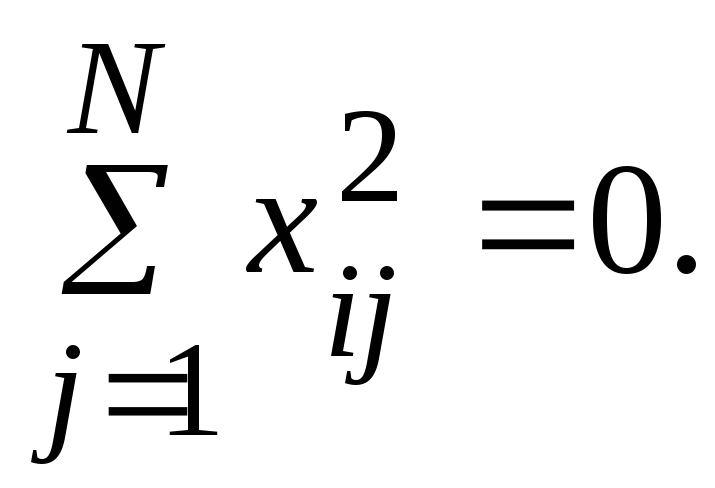
3. Свойство ортогональности - сумма построчных произведений элементов любых двух столбцов равна нулю:

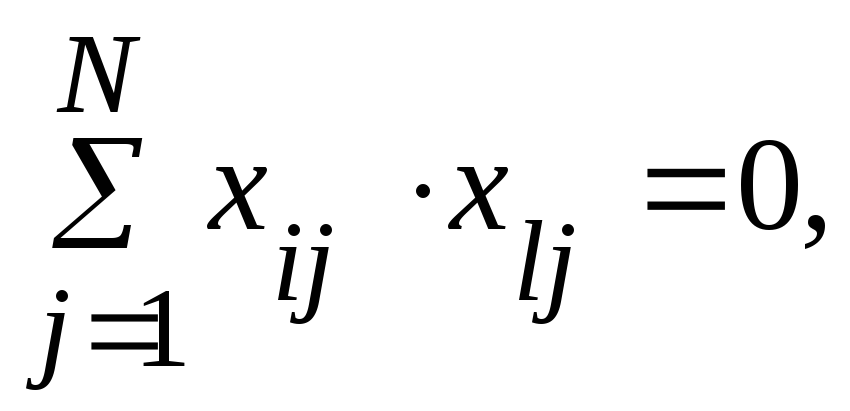
где i, l - номера факторов, причем il.

Ортогональность является одним из наиболее важных свойств матрицы. Ортогональность матрицы позволяет оценить все коэффициенты уравнения регрессии независимо друг от друга, т.е. величина любого коэффициента не зависит от того, какие величины имеют другие коэффициенты. Если какой-либо окажется незначимым, то его можно отбросить (), не пересчитывая остальных.

4. Свойство рототабельности - модель способна предсказывать значение параметра оптимизации с одинаковой точностью в любых направлениях на равных расстояниях от центра эксперимента.

Проведение эксперимента и обработка результатов опыта

После выбора плана эксперимента, основных уровней и интервалов варьирования факторов переходят к эксперименту. Каждая строка матрицы - это условия опыта. Для исключения систематических ошибок опыты рекомендуется проводить в случайной последовательности (по таблицам случайных чисел). Например, при числе опытов N=8, их последовательность будет:

Для компенсации влияния случайных погрешностей каждый опыт рекомендуется повторять n раз (параллельные или дублирующие опыты), n=2-5. Имеет место 3 варианта дублирования:

1) при равномерном дублировании опытов;

2) эксперимент проведен при неравномерном дублировании опытов;

3) эксперимент без дублирования опытов.

При (1) все строки матрицы планирования имеют одинаковое (неодинаковое - 2) число параллельных опытов, опыты не дублируются в (3). Лучший вариант - (1) - более высокая точность, простая обработка результатов.

1. Обработка результатов эксперимента при равномерном дублировании опытов.

1. Для каждой строки матрицы планирования по результатам n параллельных опытов находят - среднее параметра оптимизации:

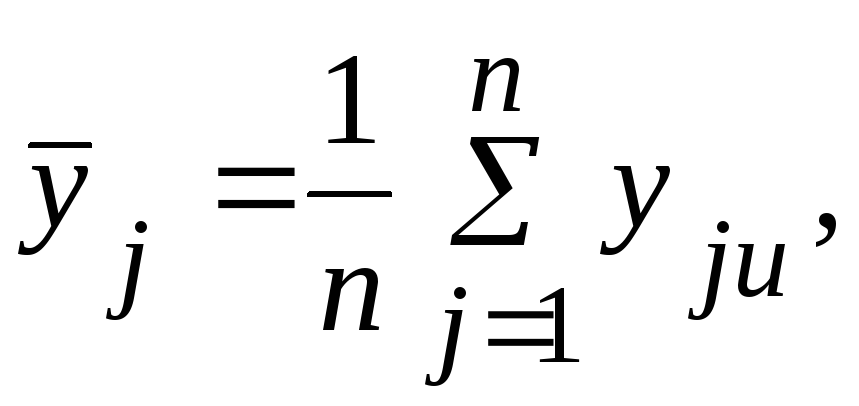(55)

где n - номер параллельного опыта; - значение параметра оптимизации в u-м параллельном опыте j-ой строки матрицы.

2. Для каждой строки матрицы определяют для n опытов дисперсию и стандарт:

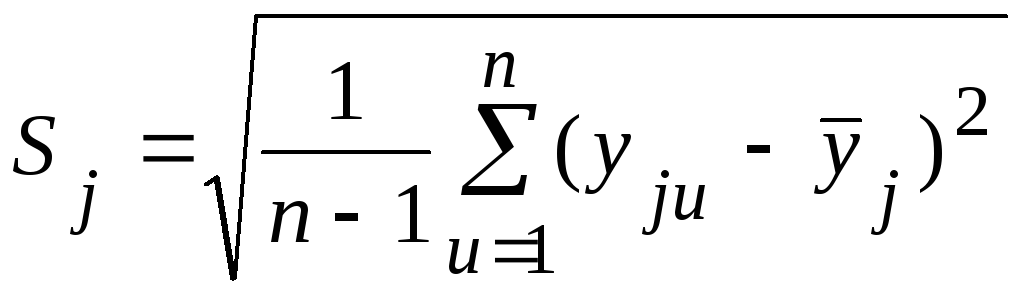(56)

Предполагая N: 0, 1 исключаются грубые ошибки (проверка на однородность по критериям 2, 3). В математической статистике для проверки гипотез пользуются критериями согласия при определенном уровне значимости q=1-p (q=1-5%), чаще q=5% (p=0,95, =0,05).

3. Проверка воспроизводимости эксперимента - это проверка выполнения предпосылки регрессионного анализа об однородности выборочных дисперсий . Проверяется гипотеза Н₀: - при опытах, соответственно в точках- равенства генеральных дисперсий. Так как все оценки дисперсий получены по выборкам одинакового объемаn, то число степеней свободы для них одинаково и равно:

(57)