Файл: лекции по планирован.эксперименту.doc

Расчет математического ожидания дискретных величин и дисперсий производится по формуле:

(20)

где x_i - случайная величина, выборка N=1r;

- вероятность каждой из точек x_i.

Нормированный показатель связи - коэффициент корреляции определяется по выражению:

(21)

По своему физическому смыслу коэффициент корреляции характеризует степень линейной зависимости между х и у и меняется в пределах Еслито случайные величины полностью положительно коррелированы, т.е.:

(22)

где а₀ и а₁ - постоянные величины, причем а₁>0.

Если то случайные величины полностью отрицательно коррелированны, т.е.:

(23)

Если то величиных и у не коррелированны (независимы), т.е. а₁=0.

При экспериментальном анализе двумерной совокупности х, у расчет оценки коэффициента корреляции производят по формуле:

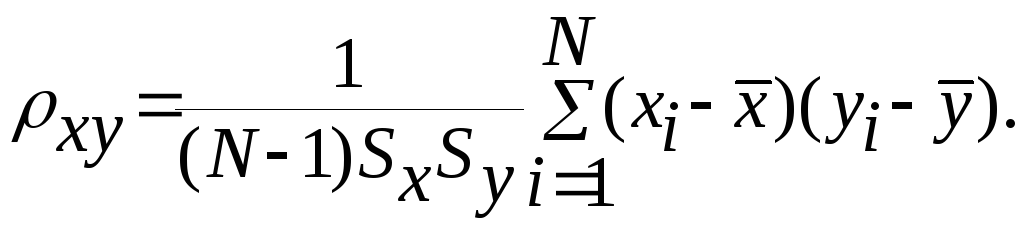(24)

В настоящее время для расчета статистических оценок разработаны стандартные программы, реализуемые на персональных компьютерах.

Если компоненты случайного вектора обозначаются одной буквой и отличаются только индексами корреляционный момент и коэффициент корреляции могут обозначаться сокращенно:и. Матрицыcov(x) и R(x) имеют следующий вид:

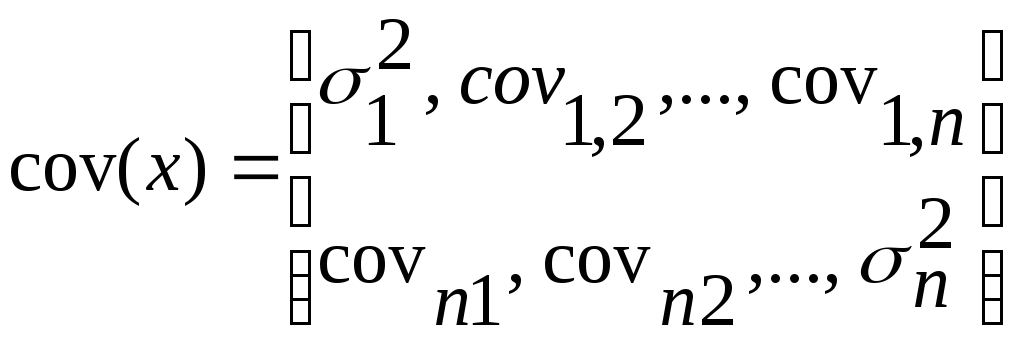(25)

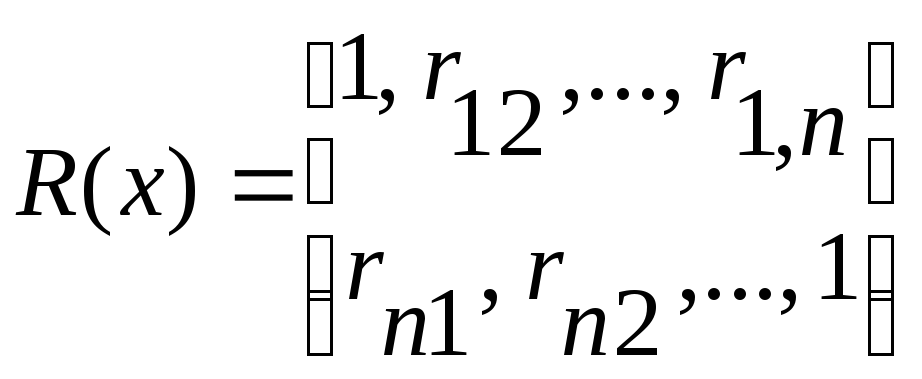(26)

Пример №2.

Расчет часов использования максимума T_max и максимальных потерь _max, как случайных величин.

В простейшем случае cos не зависит от режима и величины Т и  приближенно находятся по формулам:

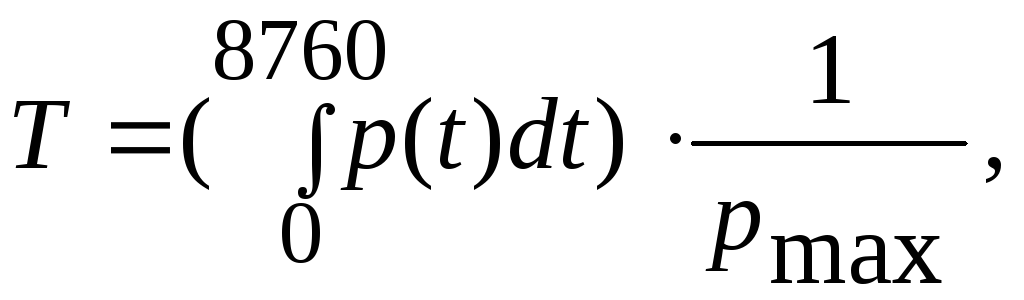(27)

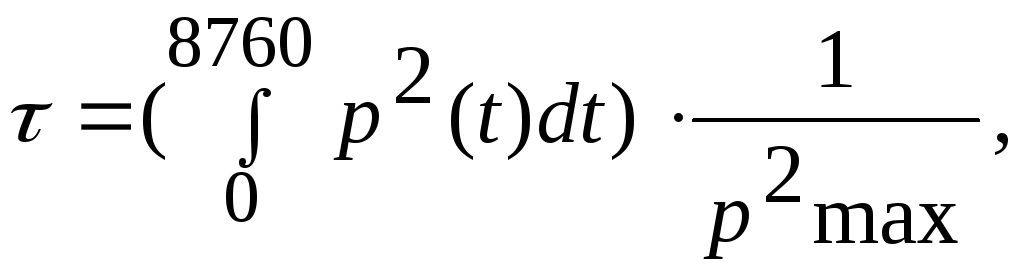(28)

Введем понятие коэффициента максимума мощности тогда:

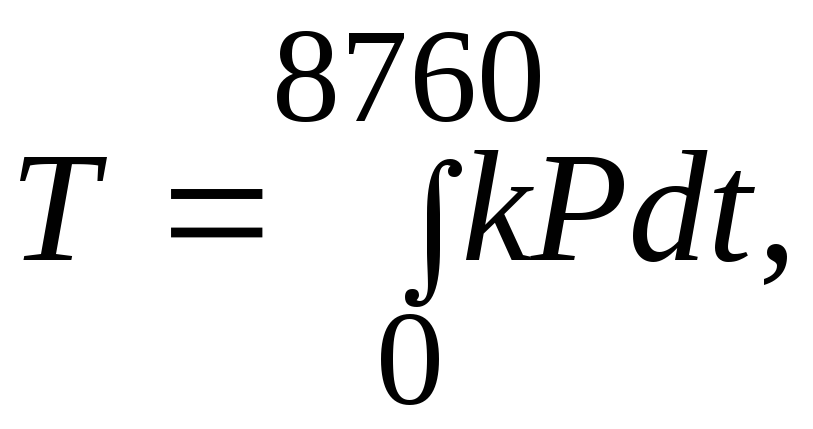
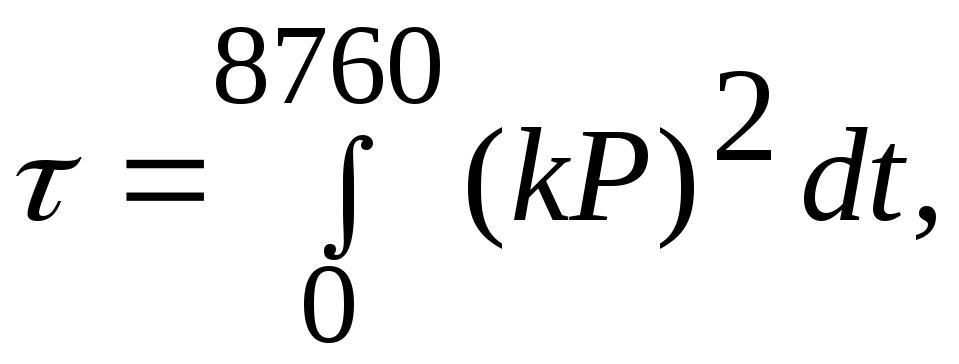(29)

Если рассматривать kP как случайную величину с областью определения на интервале 0Tmax и вероятностью каждой части  этого интервала р(), равной то математическое ожиданиеM(kP) и дисперсия могут быть рассчитаны по формулам:

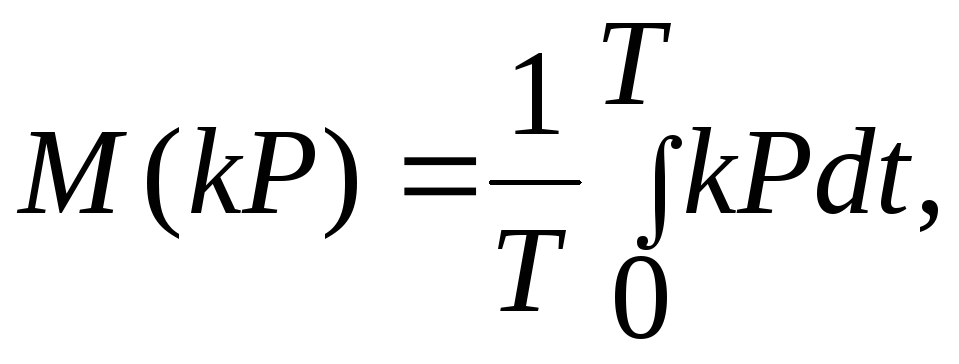(30)

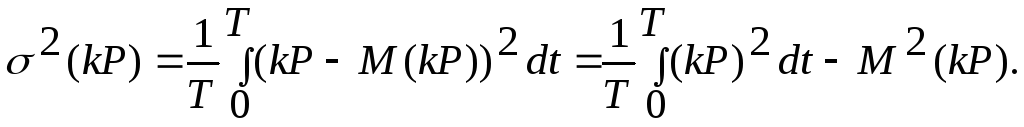(31)

Из формул (29, 30, 31) получаем соотношение математического ожидания и величин Tm и :

(32)

Таким образом Tm полностью определяется математическим ожиданием M(kP) и не зависит от дисперсии этой величины. Значение и поэтому между Tmax и  не может быть однозначной функциональной связи и разброс значений  при заданном Tmax может быть очень значительным, что видно из рис. 1.3, а, б.

На рис. 1.3 (а, б) при общем математическом ожидании имеем разные значения Тmax: Тmax=12 (Тм=Т^.М(kP)=24^.0,5=12 часов) (а) и Тmax=0.

а)

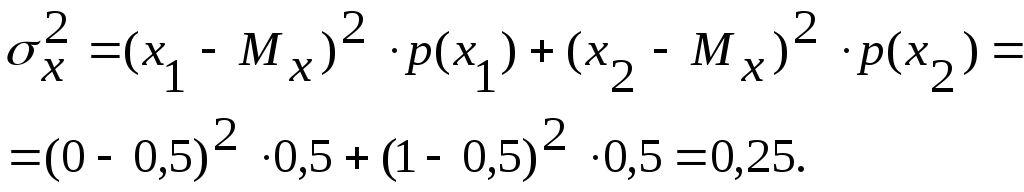
б)

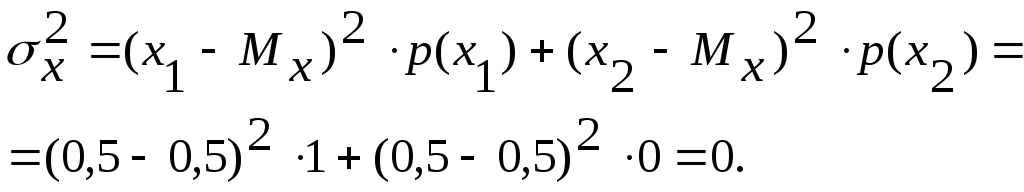
Если случайная величина х определена на дискретном вероятностном пространстве, то операция интегрирования заменяется непосредственно суммированием:

(33)

Подставляя полученные выражения в формулу для  (32) с учетом длины интервала интегрирования Т=24 часа, получим:

часов (рис. 1.3, а)

часов (рис. 1.3, б).

Таким образом, полученные результаты отличаются друг от друга в 2 раза. Приближенная зависимость между Тм и  определяется по формуле Залесского:

(34)

где 8760 - интервал интегрирования, равный одному году.

Формула (34) предложена для одно или двухсменного производства с Tmax=8 час. и Tmax=16 часов.

Пример №3.

Определить математические ожидания, дисперсии и корреляционные моменты нагрузок электрических систем.

Часть электрической системы показана на рис. 1.4.

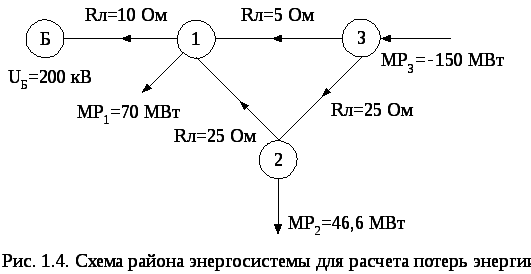
Она связывает районы потребления, нагрузка и генерация которых зависит от большого числа случайных факторов и поэтому является случайной величиной. В целях упрощения расчета рассмотрим электрическую систему постоянного тока. В базисном узле (Б) напряжение равно 200 кВ. Элементами исходного вероятностного пространства будем считать часы суток, вероятность каждого элемента - р(w_i) = 1/24, тогда множества значений случайных величин нагрузок определяются суточными графиками, показанными на рис.1.5.

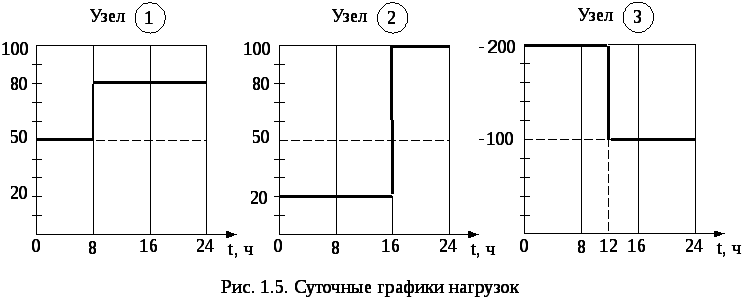
Для определения математических ожиданий и дисперсий нагрузок используем формулу:

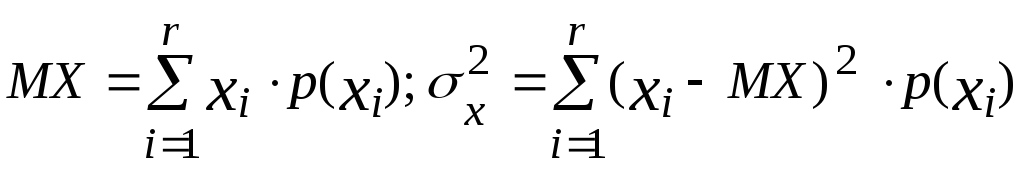(35)

Тогда:

Знак «минус» в МР₃учитывает, что в данном узле нагрузки (3) генерация энергии превышает потребление.

Дисперсии нагрузок:

;

;

.

Для определения корреляционных моментов используем формулу:

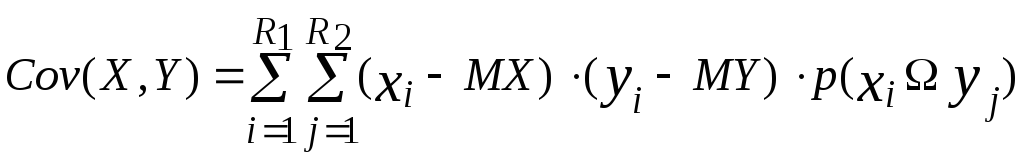, (36)

где - общая вероятность тех точек вероятностного пространства, для которых выполняются соотношения: Х(w_i) = X_i ; Y(w_j) = y_i;

w_i - точки вероятностного пространства;

R₁, R₂ - диапазоны значений случайной величины.

Остальные и определяются аналогично.

Дисперсии и корреляционные моменты образуют матрицу корреляционных моментов:

Из этой матрицы можно получить матрицу коэффициентов корреляции, используя формулу :

Вероятностный способ расчета потерь энергии

Решение задачи для реальных сетей переменного тока связано с громоздкими преобразованиями, поэтому рассмотрим упрощенную задачу: расчет потерь в сети постоянного тока.

Потеря мощности линии, соединяющей узлы i и j сети постоянного тока, имеющей проводимость , определяется по формуле:

. (37)

Для определения потерь мощности во всей сети необходимо суммировать потери по всем линиям:

.(38)

Выражение потерь мощности в окрестности точки математических ожиданий напряжений представим рядом Тейлора, в котором учтем члены первого и второго порядков малости:

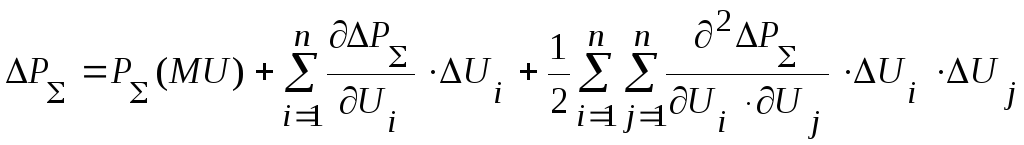.(39)

Чтобы от потерь мощности перейти к потерям энергии за интервал Т (), необходимо проинтегрировать формулу (39), что дает результат:

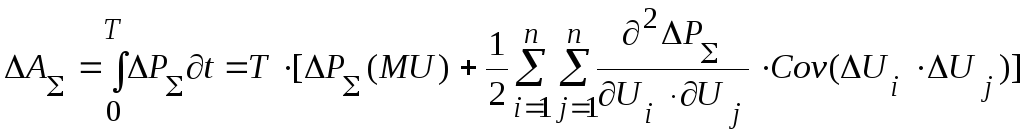,(40)

где 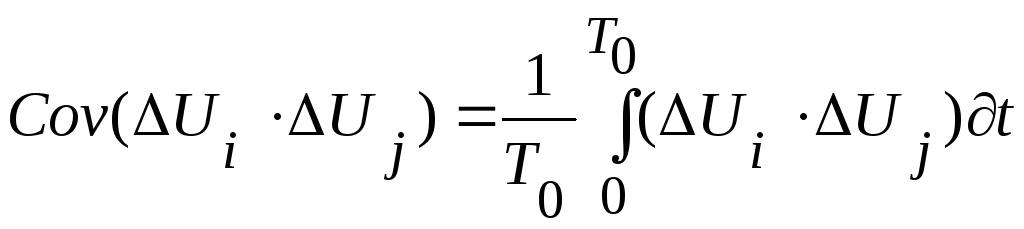- это корреляционный момент напряжений узлов i, j. В формуле выделим две составляющие:

- определяется математическим ожиданием (постоянная часть потерь энергии);

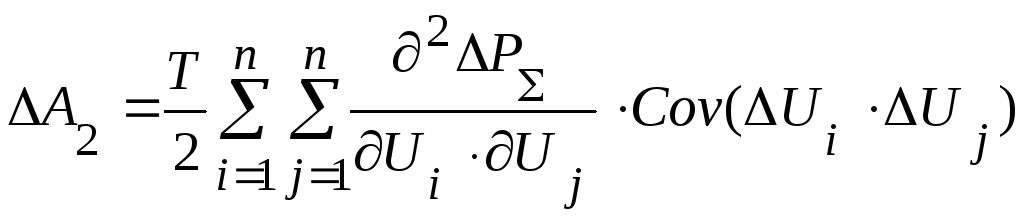- определяется колебаниями мощности в окрестности MU - дисперсионная составляющая.

Из (40) следует, что

После ряда преобразований простейшая формула для определения потерь энергии принимает вид:

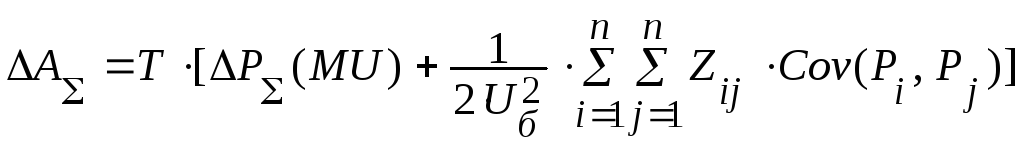(41)

Формула (41) обычно используется в численных расчетах потерь мощности и энергии.

Пример №4.