ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 175
Скачиваний: 0
СОДЕРЖАНИЕ
Министерство образования и науки
1. Основы теории инженерного эксперимента
1.1. Эксперимент как объект исследования
1.2. Основы теории обработки результатов эксперимента
Анализ и исключение грубых ошибок
Матрицы корреляционных моментов и корреляционных коэффициентов
Вероятностный способ расчета потерь энергии
Полный факторный эксперимент (пфэ)
Дробный факторный эксперимент (дфэ)
Проведение эксперимента и обработка результатов опыта
Проверка адекватности математического описания
Обработка результатов эксперимента при неравномерном дублировании опытов
Обработка результатов экспериментов при отсутствии дублирования опытов
Крутое восхождение по поверхности отклика (метод Бокса-Уилсона)
Экспериментальные планы, рекомендуемые для решения электроэнергетических задач
![]() - натуральное
значение основного уровня i-го
фактора.
- натуральное
значение основного уровня i-го
фактора.
Кодирование
позволяет значительно облегчить расчеты,
так как в этом случае нижние и верхние
уровни варьирования в относительных
единицах принимают равными:
![]() независимо от природы факторов, основных
уровней и интервалов варьирования
независимо от природы факторов, основных
уровней и интервалов варьирования![]() .
Для простоты обычно записывают + (вместо
+1) и -
вместо (-1).
.
Для простоты обычно записывают + (вместо
+1) и -
вместо (-1).
Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называют полным факторным экспериментом (ПФЭ). Если число уровней каждого фактора - m, а число факторов - k, то число всех сочетаний уровней факторов N, а, следовательно, и число опытов в ПФЭ определяется выражением:
![]() (47)
(47)
Простейшим представлением планов факторных экспериментов для построения линейных моделей является ПФЭ при 2х уровневом варьировании типа 2k. Если в эксперименте с двумя переменными х1 и х2 каждая меняется на двух уровнях (например, при расчете потерь: х1 - напряжение в узле нагрузки 105 и 120 кВ, и нагрузка 30 МВт и 60 МВт), то все возможные комбинации варьируемых факторов будут равны N=22=4 - т.е. найдены перебором из 4х опытов. ПФЭ 22 может быть представлен матрицей (табл. 1.2), в которой число строк равно количеству опытов.
Таблица 1.2
|
Номер опыта, n |
х0 |
Планирование |
х1х2 |
х12 |
х22 |
yu |
Кодовое обозначение строки |
|
|
х1 |
х2 |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
+ |
- |
- |
+ |
+ |
+ |
y1 |
1 |
|
2 |
+ |
+ |
- |
- |
+ |
+ |
y2 |
a |
|
3 |
+ |
- |
+ |
- |
+ |
+ |
y3 |
b |
|
4 |
+ |
+ |
+ |
+ |
+ |
+ |
y4 |
ab |
|
N=4 |
|
|
|
|
|
|
|
|
В табл. 1.2 верхний уровень обозначен +1 (+), нижний -1 (-). Каждая строка матрицы относится к одному из экспериментов, гр.2 - фиктивная переменная х0=+1 (+), гр.3-4 - значения х1 и х2 - собственно планирование, гр. 8 - результаты каждого опыта (yi), гр. 5-7 - значения переменных х1 и х2 - для дальнейших расчетов, гр. 9 - кодовое обозначение строк: 1 - обе переменные на нижнем уровне, ab - обе переменные на верхнем уровне, a - соответствующая переменная х1 на верхнем уровне, b - х2 на верхнем уровне.
Кодирование сокращает запись матриц. Так ПФЭ 22 записывается следующим образом: (1), a, b, ab.
При k=2 моделью будет уравнение регрессии вида:
![]() (48)
(48)
где: 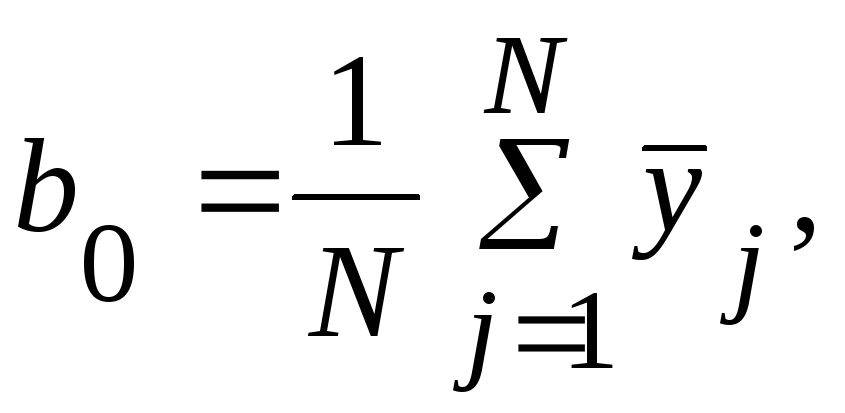 (49)
(49)
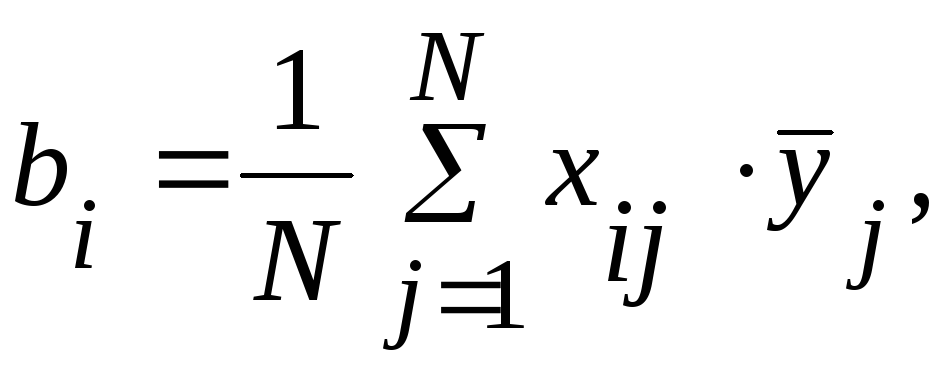 (50)
(50)
Коэффициенты регрессии, характеризующие эффекты взаимодействия:
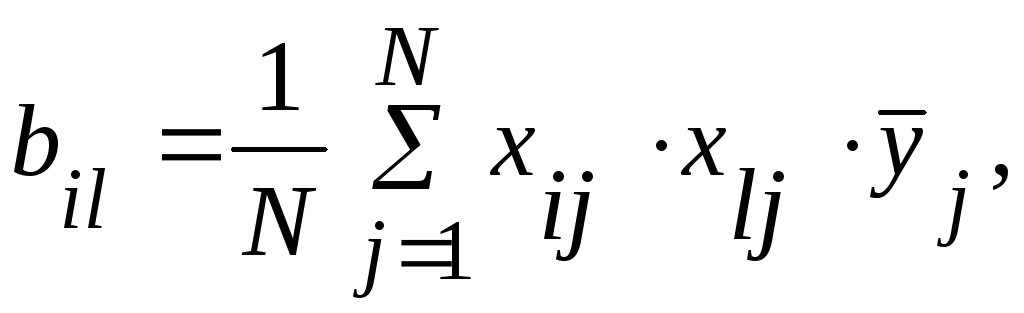 (51)
(51)
где i, l - номера факторов; хij, xlj - кодированные значения факторов i и l в j-ом опыте.
Формулы (49), (50), (51) получены по МНК.
Матрица планирования для 3х переменных на 2х уровнях получается из матрицы 22 при повторении ее дважды: один раз при значении х3 - на нижнем уровне, второй раз - на верхнем. Это формально равносильно умножению кодовой записи матрицы один раз на единицу, второй - на с. ПФЭ 23 в кодовом виде записывается: (1), a, b, ab, c, ac, bc, abc.
Схема построения матрицы при увеличении числа факторов от 2 до 3 представлена в табл. 1.3.
Таблица 1.3
|
Номер опыта |
х0 |
х1 |
х2 |
х3 |
|
1 |
+ |
+ |
+ |
+ |
|
2 |
+ |
- |
+ |
+ |
|
3 |
+ |
+ |
- |
+ |
|
4 |
+ |
- |
- |
+ |
|
5 |
+ |
+ |
+ |
- |
|
6 |
+ |
- |
+ |
- |
|
7 |
+ |
+ |
- |
- |
|
8 |
+ |
- |
- |
- |
Графическая интерпретация - куб с 8 вершинами.
С ростом числа
факторов число опытов растет по
показательной функции N=2k
и быстро наступает избыточность числа
экспериментов по отношению к числу
коэффициентов линейной модели. Если
можно ограничиться линейным приближением
модели, т.е. получить адекватную модель
в виде полинома:
![]() то число опытов можно резко сократить
в результате ДФЭ - дробного факторного
эксперимента.
то число опытов можно резко сократить
в результате ДФЭ - дробного факторного
эксперимента.
Дробный факторный эксперимент (дфэ)
Во многих практических
задачах, особенно при большом числе
факторов n
(2n)
неэффективно использовать ПФЭ, так как
в первую очередь необходимо получить
линейную аппроксимацию изучаемого
уравнения связи при минимальном
количестве экспериментов. Дробным
факторным экспериментом (ДФЭ) называется
эксперимент, реализующий часть (дробную
реплику) ПФЭ. ДФЭ позволяет получить,
например, линейное приближение искомого
функционала
![]() ,
в некоторой небольшой окрестности
базового режима при минимуме опытов,
т.е. получить адекватную модель в виде
полинома:
,
в некоторой небольшой окрестности
базового режима при минимуме опытов,
т.е. получить адекватную модель в виде
полинома:![]() (приn=2).
Так, например, при ПФЭ 22
при линейном приближении можно принять
коэффициент
(приn=2).
Так, например, при ПФЭ 22
при линейном приближении можно принять
коэффициент ![]() и тогда
и тогда ![]() .
В этом случае имеем:
.
В этом случае имеем:
![]() .
.
Для определения коэффициентов (b0, b1, b2, b3) достаточно провести 4 опыта вместо 8 опытов в ПФЭ 23. План эксперимента, предусматривающий реализацию половины опытов ПФЭ, называется полурепликой. При увеличении числа факторов k>3 возможно применение реплик большей дробности. Они обозначаются выражением 2k-p, где р - число линейных эффектов, приравненных к эффектам взаимодействия.
При р=1
получают полуреплику, при р=2
- 1/4 реплику, при р=3
- 1/8 и т.д., т.е. по степеням двойки. Так,
если при ПФЭ 23,
один из эффектов взаимодействия (![]() )
заменить на
)
заменить на![]() ,
то получим полуреплику 24-1
ПФЭ 24.
Если два эффекта взаимодействия заменить
на
,
то получим полуреплику 24-1
ПФЭ 24.
Если два эффекта взаимодействия заменить
на
![]() и
и![]() ,
то получим 1/4 реплику 25-2.
Применение ДФЭ всегда связано со
смешиванием, т.е. совместным оцениванием
нескольких теоретических коэффициентов
математической модели. Коэффициенты
b1,
b2,
b3
будут оценками совместных эффектов, а
именно, линейных эффектов и эффектов
взаимодействия.
,
то получим 1/4 реплику 25-2.
Применение ДФЭ всегда связано со
смешиванием, т.е. совместным оцениванием
нескольких теоретических коэффициентов
математической модели. Коэффициенты
b1,
b2,
b3
будут оценками совместных эффектов, а
именно, линейных эффектов и эффектов
взаимодействия.
Матрица ПФЭ типа 23 приведена в табл. 1.4.
Таблица 1.4
|
Номер опыта |
ПФЭ типа 23 |
Всп. эксп. 22 |
|||||||||
|
х0 |
х1 |
х2 |
х3 |
х1х2 |
х1х3 |
х2х3 |
х1х2х3 |
y |
х1х3 |
х2х3 |
|
|
1 |
+ |
- |
- |
+ |
+ |
- |
- |
+ |
y1 |
- |
- |
|
2 |
+ |
+ |
- |
+ |
- |
+ |
- |
- |
y2 |
- |
+ |
|
3 |
+ |
- |
+ |
+ |
- |
- |
+ |
- |
y3 |
+ |
- |
|
4 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
y4 |
+ |
+ |
|
5 |
+ |
- |
- |
- |
+ |
+ |
+ |
- |
y5 |
- |
- |
|
6 |
+ |
+ |
- |
- |
- |
- |
+ |
+ |
y6 |
- |
+ |
|
7 |
+ |
- |
+ |
- |
- |
+ |
- |
+ |
y7 |
+ |
- |
|
8 |
+ |
+ |
+ |
- |
+ |
- |
- |
- |
y8 |
+ |
+ |