ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 161
Скачиваний: 0
СОДЕРЖАНИЕ
Министерство образования и науки
1. Основы теории инженерного эксперимента
1.1. Эксперимент как объект исследования
1.2. Основы теории обработки результатов эксперимента
Анализ и исключение грубых ошибок
Матрицы корреляционных моментов и корреляционных коэффициентов
Вероятностный способ расчета потерь энергии
Полный факторный эксперимент (пфэ)
Дробный факторный эксперимент (дфэ)
Проведение эксперимента и обработка результатов опыта
Проверка адекватности математического описания
Обработка результатов эксперимента при неравномерном дублировании опытов
Обработка результатов экспериментов при отсутствии дублирования опытов
Крутое восхождение по поверхности отклика (метод Бокса-Уилсона)
Экспериментальные планы, рекомендуемые для решения электроэнергетических задач
Сравнивают ![]() с критическим
с критическим
![]() ,
где число степеней свободы=f,
которое в рассматриваемом случае
определяют по выражению:
,
где число степеней свободы=f,
которое в рассматриваемом случае
определяют по выражению: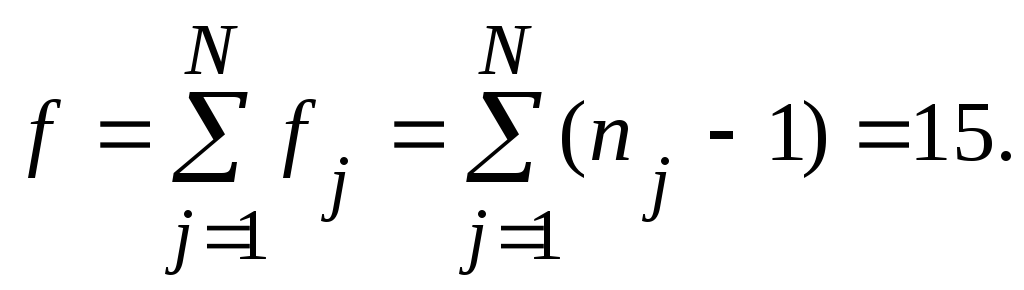
Проверяют гипотезу
Н0:
![]() (коэффициент значим) и
(коэффициент значим) и![]() (коэффициент незначим). При
(коэффициент незначим). При![]() незначимые коэффициенты могут быть
исключены из уравнения регрессии.
Оставшиеся коэффициенты пересчитывают
с использованием МНК.
незначимые коэффициенты могут быть
исключены из уравнения регрессии.
Оставшиеся коэффициенты пересчитывают
с использованием МНК.
6. Определяют дисперсию адекватности:
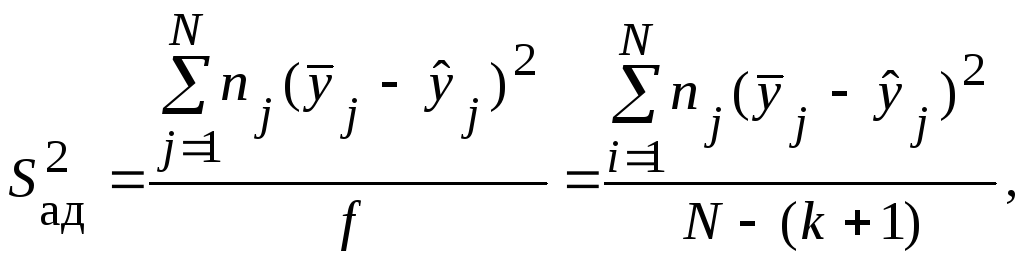
![]() - число параллельных
опытов в j-ой
строке матрицы; k
- число факторов.
- число параллельных
опытов в j-ой
строке матрицы; k
- число факторов.
7. Проверяют гипотезу адекватности модели по F-критерию Фишера:
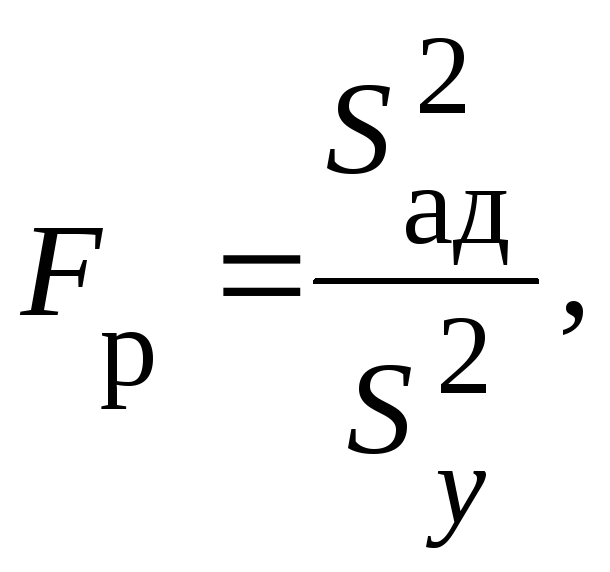
Если Н0:![]() ,
то модель адекватна. Если
,
то модель адекватна. Если ![]() - то гипотеза Н0
отвергается.
- то гипотеза Н0
отвергается.
Обработка результатов экспериментов при отсутствии дублирования опытов
Алгоритм расчета.
1. Для вычисления
дисперсии ![]() воспроизводимости эксперимента выполняют
несколько параллельных опытов в нулевой
точке (центре плана). При этом все факторы
находятся на нулевых уровнях. По
результатам опытов в центре плана
вычисляют дисперсию
воспроизводимости эксперимента выполняют
несколько параллельных опытов в нулевой
точке (центре плана). При этом все факторы
находятся на нулевых уровнях. По
результатам опытов в центре плана
вычисляют дисперсию ![]() воспроизводимости экспериментов:
воспроизводимости экспериментов:
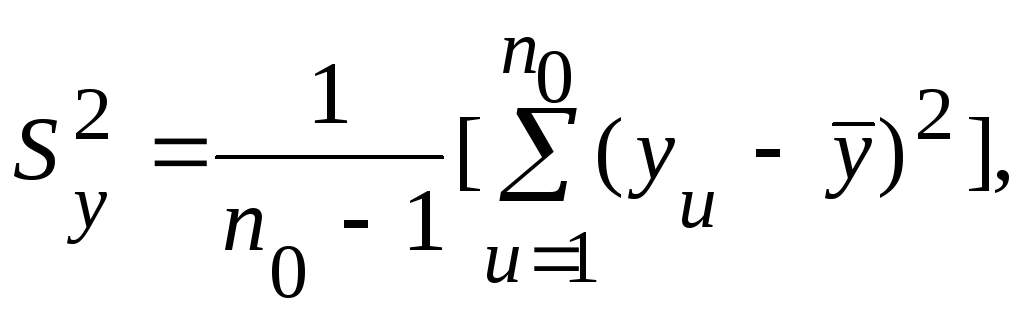 (69)
(69)
где ![]() - число параллельных опытов в нулевой
точке;
- число параллельных опытов в нулевой
точке;
![]() - значение параметра
оптимизации в u-м
опыте;
- значение параметра
оптимизации в u-м
опыте;
![]() - среднее значение
в
- среднее значение
в ![]() параллельных опытах.
параллельных опытах.
2. Определяют коэффициенты модели.
Свободный член:
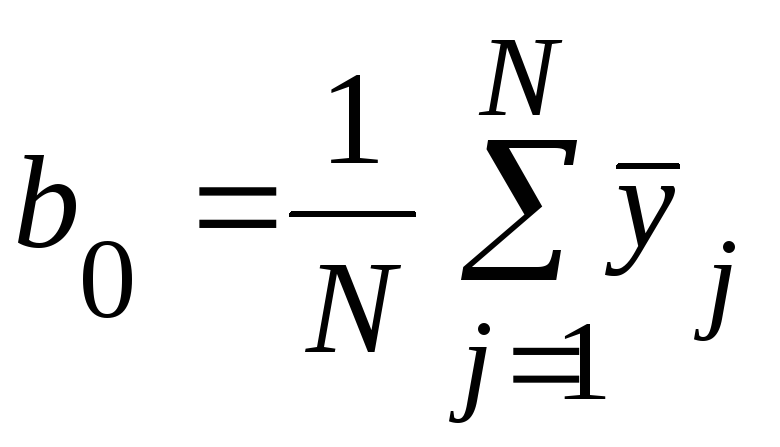 .
.
Линейные эффекты:
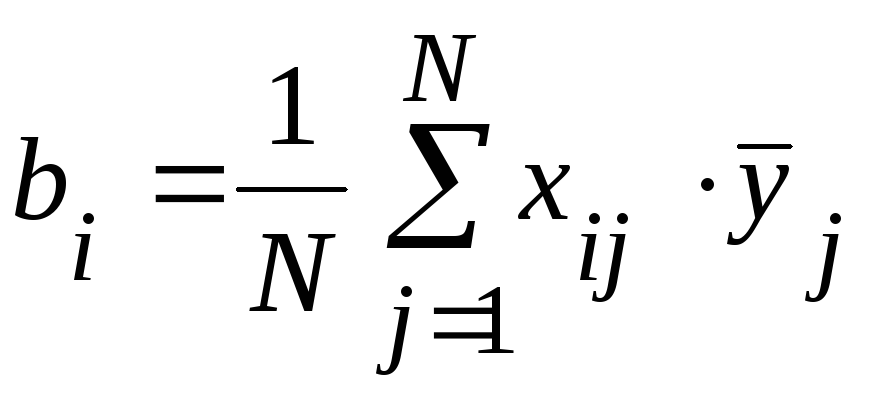 .
.
Эффекты взаимодействия:
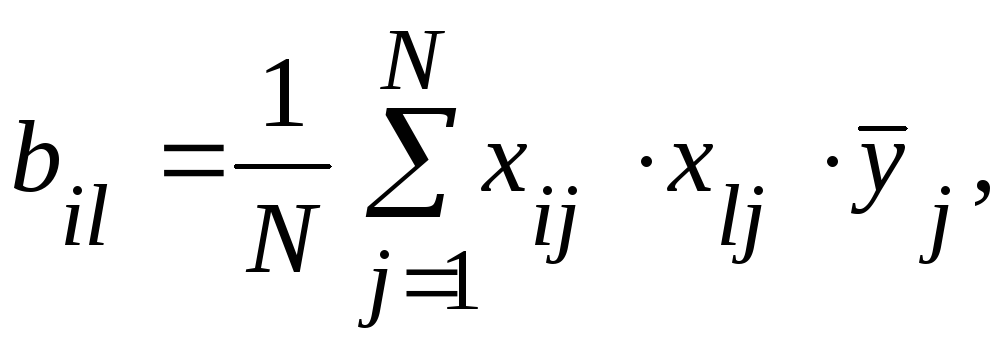
где i,
l
- номера факторов; j
- номер строки или опыта в матрице
планирования;![]() - значение параметра оптимизации в j-м
опыте;
- значение параметра оптимизации в j-м
опыте;![]() ,
,
![]() - кодированные значения (1)
факторов i
и l
в j-м
опыте.
- кодированные значения (1)
факторов i
и l
в j-м
опыте.
3. Статистическая
значимость
![]() :
:
а) сравнение
абсолютной величины
![]() с доверительным интервалом, для построения
которого определяют дисперсию
с доверительным интервалом, для построения
которого определяют дисперсию![]() :
:
![]() (70)
(70)
где ![]() - дисперсия i-го
коэффициента регрессии; N
- число строк или опытов в матрице
планирования.
- дисперсия i-го
коэффициента регрессии; N
- число строк или опытов в матрице
планирования.
Из (70) следует, что
![]()
Доверительный
интервал
![]() равен:
равен:![]()
где ![]() - табличное значение критерия Стьюдента
при =0,05
и
- табличное значение критерия Стьюдента
при =0,05
и
![]() .
.
Проверяется
гипотеза Н0:
![]() - коэффициент регрессии значим, при
- коэффициент регрессии значим, при![]() - незначим и исключается из уравнения
регрессии;
- незначим и исключается из уравнения
регрессии;
б) с помощью t-критерия Стьюдента.
Расчетное значение:
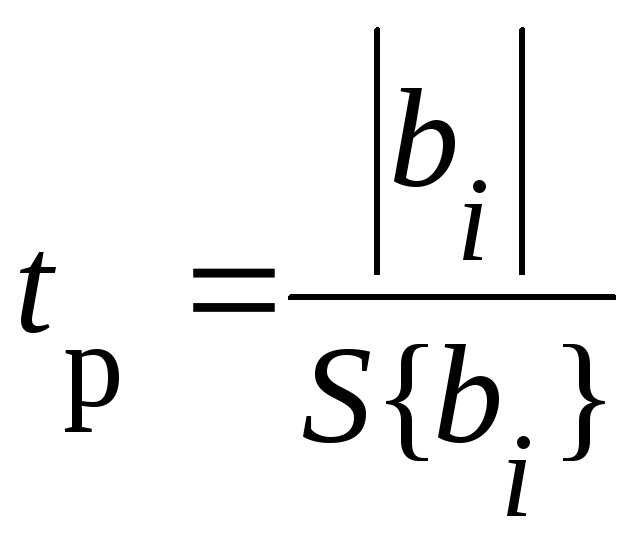 .
Гипотеза Н0:
.
Гипотеза Н0:
![]() -
-![]() значимы, если
значимы, если![]() - то коэффициенты
- то коэффициенты![]() незначимы.
незначимы.
4. Определяют
дисперсию адекватности ![]() по формуле:
по формуле:
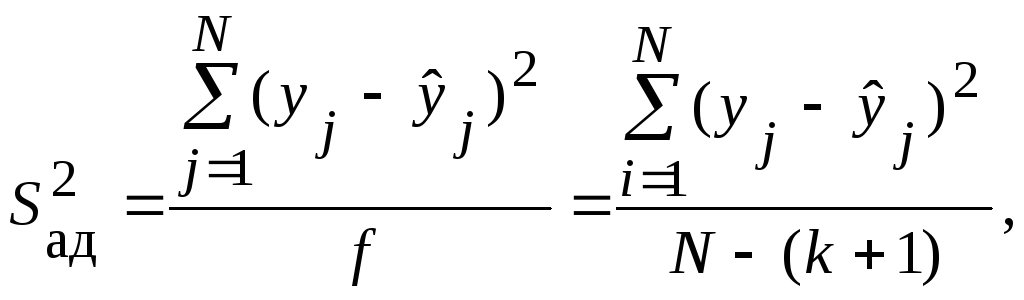 (71)
(71)
где ![]() - наблюдаемое значение параметра в j-м
опыте;
- наблюдаемое значение параметра в j-м
опыте;
![]() - значение параметра,
вычисленное по модели для условий j-го
опыта;
- значение параметра,
вычисленное по модели для условий j-го
опыта;
f - число степеней свободы.
5. Проверяют гипотезу
адекватности модели по F-критерию
Фишера (60). Если подтверждается гипотеза
Н0:![]() ,
то модель адекватна. Если
,
то модель адекватна. Если ![]() ,
то гипотеза Н0
отвергается. В этом случае:
,
то гипотеза Н0
отвергается. В этом случае:
а) переходят к планированию 2го и более высокого порядка эксперимента;
б) уменьшают
интервалы варьирования
![]() и повторяют эксперимент.
и повторяют эксперимент.
Если линейная
модель адекватна, то переходят к методу
крутого восхождения для оптимизации
параметров. При этом все
![]() должны быть значимыми. В случае если
все
должны быть значимыми. В случае если
все![]() кроме
кроме![]() незначимы, то следует:
незначимы, то следует:
1) рассмотреть интервалы варьирования;
2) повысить точность эксперимента путем улучшения методики и увеличения числа параллельных опытов.
Крутое восхождение по поверхности отклика (метод Бокса-Уилсона)
Градиентом
называется вектор, показывающий
направление наискорейшего изменения
некоторой величины, значение которой
меняется от одной точки пространства
к другой. Градиент (![]() )
непрерывной однозначной функции
)
непрерывной однозначной функции![]() есть вектор:
есть вектор:
![]()
где ![]() - частная производная функции по i-му
фактору;
- частная производная функции по i-му
фактору;
![]() - единичные вектора
в направлении осей факторов.
- единичные вектора
в направлении осей факторов.
Согласно теореме Тейлора о разложении аналитической функции в ряд, частные производные по факторам равны по величине и знаку соответствующим коэффициентам регрессии.
Следовательно,
градиент
![]() функцииу
есть вектор:
функцииу
есть вектор:
![]()
Движение по
градиенту - кратчайший путь к оптимуму,
так как направление градиента - это
направление самого крутого склона,
ведущего от данной точки к вершине. Если
изменять факторы пропорционально их
коэффициентам с учетом знака, то движение
к оптимуму называется крутым восхождением.
Технику расчета крутого восхождения
рассмотрим на примере задачи с одним
фактором
![]() (рис. 1.7).
(рис. 1.7).
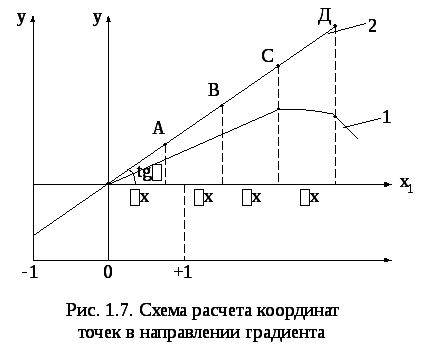
1 - график неизвестной функции отклика;
2 - прямая
![]() - направление градиента адекватно
описывающее функцию отклика в областих,
от -1
до +1.
- направление градиента адекватно
описывающее функцию отклика в областих,
от -1
до +1.
![]() ,
шаг движениях,
тогда координаты точки А:
,
шаг движениях,
тогда координаты точки А:
![]() (лежит на градиенте),В:
(
(лежит на градиенте),В:
(![]() ),
С:
(
),
С:
(![]() )
и т.д.
)
и т.д.
Затем проводят опыты с условиями, отвечающими точкам на градиенте. По результатам этих опытов определяют область оптимума. Обычно проводят часть опытов, чтобы оптимум получить в «вилке» (между точками СД).
В случае k
факторов расчет крутого восхождения
по оси каждого фактора проводят
аналогично, так как коэффициенты
![]() определяются независимо друг от друга.
Движение осуществляют одновременно.
определяются независимо друг от друга.
Движение осуществляют одновременно.
Шаг движения по
градиенту выбирают для одного фактора,
так, чтобы
![]() где
- ошибка, с которой фиксируют фактор.
Для остальных факторов шаг определяют
по выражению:
где
- ошибка, с которой фиксируют фактор.
Для остальных факторов шаг определяют
по выражению:
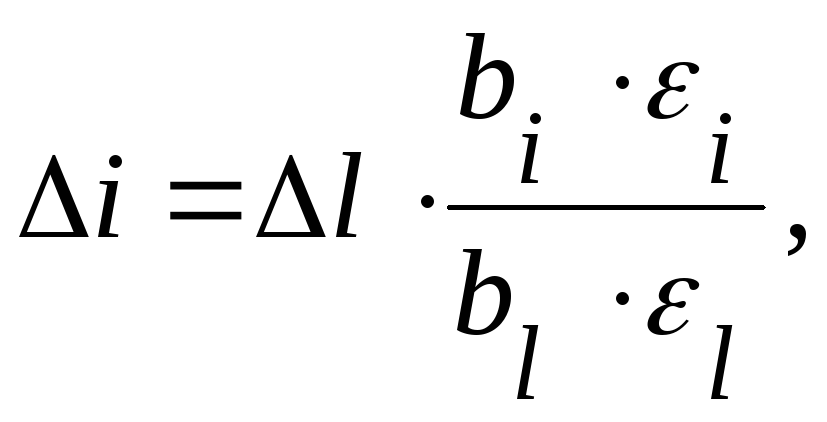
где l - выбранный шаг движения для фактора l;
i - шаг движения для i-го фактора;
![]() - коэффициенты
регрессии i-го
и l-го
факторов;
- коэффициенты
регрессии i-го
и l-го
факторов;
![]() - интервалы
варьирования i-го
и l-го
факторов.
- интервалы
варьирования i-го
и l-го
факторов.
Движение по
градиенту начинается с нулевой точки
(уровня). Если
![]() значительно различны (на порядок), то
следует изменить интервалы варьирования
факторов и повторить опыты.
значительно различны (на порядок), то
следует изменить интервалы варьирования
факторов и повторить опыты.