ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.04.2024
Просмотров: 4543
Скачиваний: 0
СОДЕРЖАНИЕ
2.1. Файловая структура, файлы, папки
2.2. Работа с программой Проводник
2.2.1. Навигация по файловой структуре
2.2.2. Запуск программ и открытие документов
2.2.4. Копирование и перемещение файлов и папок
2.2.5. Удаление файлов и папок
2.2.6. Создание ярлыков файлов, представление объектов
2.2. Содержимое стандартного набора вкладок
2.3. Ввод, редактирование, форматирование и рецензирование текста
2.4. Основы работы с таблицами
2.6. Сохранение и печать созданного документа
Основы работы с пакетом Microsoft Excel
2.2 Создание электронных таблиц пакетом Microsoft Excel
Ввод, редактирование и форматирование данных
Вычисления в электронных таблицах
Использование стандартных функций
Построение диаграмм и графиков
2.3 Сохранение и печать созданной книги
2.2. Основные этапы составления программы
2.3. Оформление окна программы (размещение компонентов на форме)
2.4. Назначение и основные свойства некоторых компонентов
Компонент Memo (Многострочный текстовый редактор)
Компонент ComboBox (Блок с комбинированным раскрывающимся списком)
2.2. Создание заготовок процедур-обработчиков событий. Текст модуля программы
2.2. Оформление окна программы
2.3. Изменение свойств компонентов. Получение заготовки процедуры
2.4. Программирование вычислений определенных интегралов
2.1.2. Сложение и вычитание матриц
2.1.3. Умножение матрицы на число
2.1.5. Транспонирование матрицы
2.1.6. Линейные преобразования
2.2 Массивы и переменные с индексами
2.3. Составление программ реализующих основные матричные операции
Оформление эскиза окна программы
x:=a+h;
for i:=1 to n-1 do
begin
s:=s+x*x*sqrt(1-x*x);
x:=x+h;
end;
s:=h*s;
Edit4.Text:=FloatToStr(s);
end; // Конец описания процедуры
end. // Конец модуля
Задание 2. Составить программу вычисления определенного интеграла
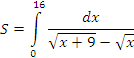
по формуле (4), приняв n=350.
При выполнении этого задания оформление окна программы, изменение свойств компонентов и получение заготовки процедуры-обработчика события OnClick проведем согласно описанному в п.п. 2.2, 2.3. Программирование вычисления этого интеграла по формуле (6.4) сведем к вводу с клавиатуры в полученную заготовку описаний типов переменных и операторов по аналогии с выполнением задания 1. При этом в тексте процедуры необходимо изменить только два оператора:
- оператор, реализующий вычисление полусуммы (y0+yn)/2:
s:=(1.0/(sqrt(a+9) - sqrt(a))+1.0/(sqrt(b+9)-sqrt(b)))/2.0;
- оператор, реализующий в цикле вычисление частных сумм и полной суммы ординат:
s:=s+1.0/(sqrt(x+9)-sqrt(x));
В результате проведенных изменений, текст процедуры-обработчика события может иметь следующий вид:
procedure TForm1.Button1Click(Sender: TObject); // Заголовок процедуры
var
i,n:integer;
a,b,s,h,x:real;
begin
a:=StrToFloat(Edit1.Text);
b:=StrToFloat(Edit2.Text);
n:=StrToInt(Edit3.Text);
h:=(b-a)/n;
s:=(1.0/(sqrt(a+9) - sqrt(a))+1.0/(sqrt(b+9)-sqrt(b)))/2.0;
x:=a+h;
for i:=1 to n-1 do
begin
s:= s+1.0/(sqrt(x+9)-sqrt(x));
x:=x+h;
end;
3. Выполнение работы
1. Включите ПК, создайте две папки для хранения двух проектов.
2. Запустите систему Delphi.
3. Выполните каждый пункт задания 1 и сохраните проект в 1-й папке. Откомпилируйте и запустите на выполнение составленную программу ЩЛК на командах:
<Run>→<Run>.
При необходимости, проведите отладку программы.
3.4. Повторите перечисленное в п.3.3 для задания 2.
4. Форма отчета
Отчет должен содержать:
- основные положения по пунктам 2.1 - 2.4;
- для первого задания: условие задания; окно проекта и модуль с комментариями;
- для второго задания: условие задания; окно проекта и текст процедуры - обработчика события с комментариями.
5. Контрольные вопросы
1. Поясните геометрический смысл определенного интеграла.
2. Приведите вывод формулы трапеции.
3. Какие преобразования реализуют стандартные функции с именами StrToFload, StrToInt, FloatToStr, IntToStr?
4. Поясните текст модуля задания 1.
5. Вычисление каких математических величин реализует каждый оператор в процедуре-обработчике события второго задания?
6. Литература
1. Фаронов В.В. Delphi. Программирование на языке высокого уровня. Учебник для вузов. – СПб.: Питер, 2007. – 640 с.
Лабораторная работа №7
Составление, ввод, трансляция, отладка и исполнение программ, реализующих основные матричные операции
1. Цель работы: изучить приемы объектно-ориентированного программирования для реализации основных матричных операций; закрепить полученные знания на конкретных примерах.
2. Основные положения
2.1.Матрицы и основные операции над ними
В инженерной практике матричный аппарат часто применяется для построения математических моделей электронных схем. Первоначально матрицы были введены для упрощения записи систем линейных уравнений, что обусловило и определение основных матричных операций.
2.1.1. Типы матриц
Матрица – это совокупность таблично упорядоченных чисел или объектов другой природы, расположенных в виде прямоугольной таблицы:
|
а11 |
а12 |
а13 |
а14 |
|
а21 |
а22 |
а23 |
а24 |
|
а31 |
а32 |
а33 |
а34 |
|
а41 |
а42 |
а43 |
а44 |
А=
Такая таблица, состоящая из m строк и n столбцов, имеет размер m*n. Числа или любые другие объекты, расположенные на пересечении i-ой строки и j-ого столбца, называют элементами матрицы и обозначают aij. Часто матрица формально обозначается так:
A={aij}, i=1,2,…, m; j=1,2,…,n.
При этом первый индекс i всегда указывает номер строки, а второй j – номер столбца.
Матрицы, элементами которых являются целые или вещественные числа, называют соответственно целыми или вещественными.
Если матрица состоит из одного столбца или одной строки, то она соответственно называется матрицей-столбцом (вектором-столбцом) или матрицей-строкой (вектором-строкой) и сокращенно обозначается: x(x1,x2,…,xm) и a(a1,a2,…,an).
Матрица, количество строк и столбцов которой одинаково и равно n, называется квадратной матрицей порядка n. Совокупность элементов aii(i=1,2,3,…,n) образует главную диагональ квадратной матрицы.
Матрица, все элементы которой вне главной диагонали равны 0, называется диагональной и кратко записывается:
D=diag{d1, d2,…,dn).
Если в диагональной матрице все элементы равны 1, то имеем единичную матрицу n-го порядка, она часто обозначается En.
Квадратная матрица называется верхней (нижней) треугольной, если равны нулю все элементы, расположенные под (над) главной диагональю.
2.1.2. Сложение и вычитание матриц
Сумма 2-х матриц A={aij} и B={bij} (i=1,2,3,…,m; j=1,2,3,…,n) одинаковых размеров определяется как матрица C={cij) тех же размеров, каждый элемент которой равен сумме соответствующих элементов матриц т.е.
cij=aij+ bij. (7.1)
Формально операция сложения матриц A и B записывается так:
C=A+B (7.2)
Операция сложения матриц коммутативна, т.е. A+B=B+A, и ассоциативна, т.е. (A+B)+C=A+(B+C). Эта операция распространяется на любое число слагаемых.
Разность 2-х матриц A={aij} B={bij} (i=1,2,3,…,m; j=1,2,3,…,n) одинаковых размеров определяется как матрица C={cij} тех же размеров, каждый элемент которой определяется:
cij= aij – bij. (7.3)
Формально операция вычитания записывается так:
C=A–B. (4).
2.1.3. Умножение матрицы на число
В отличие от матриц и векторов, числа часто называют скалярами.
Произведением матрицы A на число β является матрица C=β*A, элементы которой получаются умножением соответствующих элементов матрицы A на это число β, т.е. cij=β*aij. Общий множитель элементов можно выносить за знак матрицы, считая его скалярным множителем.
2.1.4. Умножение матриц
Произведением матрицы A размера (m*n) на матрицу B размера (n*r) является матрица C=A*B размера (m*r), элемент cij которой, расположенный в ij-клетке, равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B, т.е.
cij
=ai1b1j
+ ai2
b2j
+…+ ain
bnj
=
![]() aik
bkj
. (7.5)
aik
bkj
. (7.5)
Умножение А на В допустимо (произведение А*В существует),если число столбцов А равно числу строк В. В таких случаях говорят, что эти две матрицы согласуются по форме.
Для матриц А={aij}(i =1,2,3, … ,m; j=1,2,3, … , n) и В ={ bij } (i = 1,2,3, … , n ; j =1,2,3, … , m) существует как произведение А*В размера m*m, так и произведение В*А размера n*n. При m ≠ n эти произведения не могут быть равными вследствие различных размеров результирующих матриц.
Для квадратных матриц одинакового порядка (при m = n) произведение А*В и В*А не обязательно равны между собой. Если А*В = В*А, то матрицы А и В называются коммутирующими или перестановочными. Поэтому различают умножение матрицы А на В справа (А*В) и слева (В*А).
Умножение матрицы А = { aij} (i=1,2,3, … , m ; j = 1,2,3, … , n) на единичную матрицу n-го порядка (Еn) справа и на единичную матрицу m-го порядка (Еm) слева не изменяет этой матрицы, т.е.
A*En = Em *A = A.
2.1.5. Транспонирование матрицы
Преобразование матрицы А, состоящее в замене строк столбцами (или столбцов строками) при сохранении их нумерации, называется транспонированием. Полученная в результате такого преобразования матрица называется транспонированной к матрице А и обозначается АT.
Произвольная (m*n) – матрица при транспонировании становится (n*m) – матрицей, а элемент aij занимает ji – клетку т. е.
аij =аТji .
Получение матрицы B={bij} (i = 1,2, … , n; j = 1,2, … , m) транспонированной к A = {aij} (i = 1,2, … , m; j = 1,2,… , n) сводится к определению её элементов так:
bij = aji. (7.6)
Если квадратная матрица совпадает со своей транспонированной, т.е. А=АТ ,
то, она называется симметричной и её элементы связаны соотношением aij=aji (симметрия относительно главной диагонали).