ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.04.2024
Просмотров: 4570
Скачиваний: 0
СОДЕРЖАНИЕ
2.1. Файловая структура, файлы, папки
2.2. Работа с программой Проводник
2.2.1. Навигация по файловой структуре
2.2.2. Запуск программ и открытие документов
2.2.4. Копирование и перемещение файлов и папок
2.2.5. Удаление файлов и папок
2.2.6. Создание ярлыков файлов, представление объектов
2.2. Содержимое стандартного набора вкладок
2.3. Ввод, редактирование, форматирование и рецензирование текста
2.4. Основы работы с таблицами
2.6. Сохранение и печать созданного документа
Основы работы с пакетом Microsoft Excel
2.2 Создание электронных таблиц пакетом Microsoft Excel
Ввод, редактирование и форматирование данных
Вычисления в электронных таблицах
Использование стандартных функций
Построение диаграмм и графиков
2.3 Сохранение и печать созданной книги
2.2. Основные этапы составления программы
2.3. Оформление окна программы (размещение компонентов на форме)
2.4. Назначение и основные свойства некоторых компонентов
Компонент Memo (Многострочный текстовый редактор)
Компонент ComboBox (Блок с комбинированным раскрывающимся списком)
2.2. Создание заготовок процедур-обработчиков событий. Текст модуля программы
2.2. Оформление окна программы
2.3. Изменение свойств компонентов. Получение заготовки процедуры
2.4. Программирование вычислений определенных интегралов
2.1.2. Сложение и вычитание матриц
2.1.3. Умножение матрицы на число
2.1.5. Транспонирование матрицы
2.1.6. Линейные преобразования
2.2 Массивы и переменные с индексами
2.3. Составление программ реализующих основные матричные операции
Оформление эскиза окна программы
Определенный интеграл
![]() (6.1)
(6.1)
представляет
собой площадь,
ограниченную кривой подинтегральной
функции ![]() ,
осью абсцисс и прямыми
,
осью абсцисс и прямыми ![]() и
и ![]() (см. рис. 6.1).
(см. рис. 6.1).
Обычно,
обозначают ![]() Для вычисления искомой площади, отрезок
Для вычисления искомой площади, отрезок
![]() разбивают на
разбивают на ![]() интервалов, каждый величиной
интервалов, каждый величиной
![]() (6.2)
(6.2)
которая
называется шагом
интегрирования.
На каждом интервале, величиной
h,
площадь ‘элементарной’ фигуры,
ограниченной кривой подинтегральной
функции ![]() ,
2-мя ординатами (например,
,
2-мя ординатами (например, ![]() и
и ![]() )
и осью абсцисс, заменяют площадью,
ограниченной прямой, теми же ординатами
и осью абсцисс, т.е. площадью ‘элементарной’
трапеции. Отсюда следует название –
метод трапеций.
В целом, на отрезке
)
и осью абсцисс, заменяют площадью,
ограниченной прямой, теми же ординатами
и осью абсцисс, т.е. площадью ‘элементарной’
трапеции. Отсюда следует название –
метод трапеций.
В целом, на отрезке ![]() кривая подинтегральной функции
кривая подинтегральной функции ![]() заменяется (аппроксимируется)
кусочно-линейной функцией (см. рис. 6.1).
заменяется (аппроксимируется)
кусочно-линейной функцией (см. рис. 6.1).
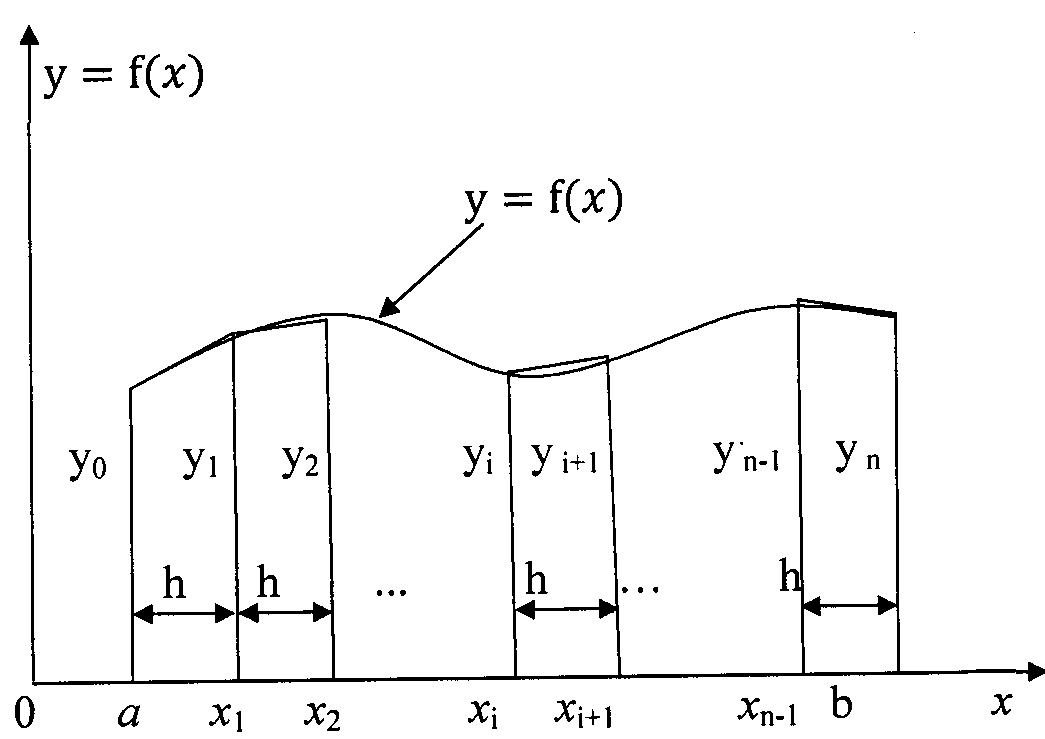
Рис. 6.1. Геометрический смысл определенного интеграла.
Площадь
‘элементарной’ трапеции ![]() для интервала с номером
для интервала с номером
![]() вычисляется по формуле:
вычисляется по формуле:
![]() (6.3)
(6.3)
а
площадь, ограниченная кривой подынтегральной
функции ![]() осью абсцисс и ординатами
осью абсцисс и ординатами ![]() и
и ![]() ,
приближенно будет равна сумме площадей
‘элементарных’ трапеций. Тогда можно
записать:
,
приближенно будет равна сумме площадей
‘элементарных’ трапеций. Тогда можно
записать:
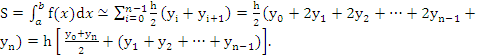 (6.4)
(6.4)
Эту запись называют формулой трапеций. В формуле (6.4) последняя форма записи является удобной для составления программ на алгоритмических языках.
2.2. Оформление окна программы
Окно
программы должно быть ‘понятным’ для
пользователей и аккуратно оформленным.
Исходными данными для программы являются:
a
– нижний
предел интегрирования, b
– верхний предел, n
– число разбиений отрезка ![]() .
Результатом вычислений является значение
переменной S,
вычисленное по формуле (6.4). Поэтому в
эскизе окна программы предусмотрим 4
надписи, поясняющие, где вводятся
.
Результатом вычислений является значение
переменной S,
вычисленное по формуле (6.4). Поэтому в
эскизе окна программы предусмотрим 4
надписи, поясняющие, где вводятся ![]() и где отображается результат счета S.
Для этого используем 4 компонента
Label1,…,Label4.
Разместим эти компоненты с одинаковой
высотой и шириной в левой части эскиза
окна.
и где отображается результат счета S.
Для этого используем 4 компонента
Label1,…,Label4.
Разместим эти компоненты с одинаковой
высотой и шириной в левой части эскиза
окна.
Ввод
значений ![]() а также вывод полученного результата
будем осуществлять, используя компоненты
Edit1,…,Edit4,
являющиеся однострочными редакторами
текста. Разместим эти компоненты правее
соответствующим им меткам Label1,…,Label4
и установим им одинаковую высоту и
ширину.
а также вывод полученного результата
будем осуществлять, используя компоненты
Edit1,…,Edit4,
являющиеся однострочными редакторами
текста. Разместим эти компоненты правее
соответствующим им меткам Label1,…,Label4
и установим им одинаковую высоту и
ширину.
Вычисления по формуле (6.4) будут производиться при ЩЛК на командной кнопке Button1. Разместим Button1 ниже компонентов Label4 и Edit4 по центру эскиза окна программы.
При необходимости можно изменить положение пар Label1 – Edit1,…, Label4 – Edit4, выравнивая их по горизонтали и располагая симметрично относительно вертикальной оси по центру окна. В результате получим один из вариантов эскиза окна, представленный на рис. 6.2.
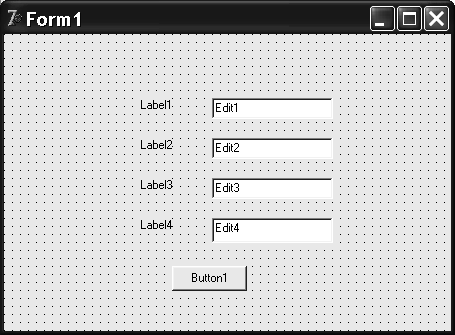
Рис. 6.2. Эскиз окна программы.
2.3. Изменение свойств компонентов. Получение заготовки процедуры
В окне ‘Object Inspector’ (пер. ‘Инспектор объекта’) зададим основные свойства каждому компоненту окна. Свойству Caption компонента Form1 зададим значение ‘Метод трапеций’. Свойству Caption каждого компонента Label1, Label2, Label3, Label4 зададим соответственно значения: ‘Введите а =’, ‘Введите b =’, ‘Введите n =’, ‘Результат S =’. Это подсказки пользователю: что вводить в поля редакторов текста Edit1, Edit2, Edit3 перед ЩЛК на кнопке Button1, и что будет выведено в поле редактора Edit4 после ЩЛК на Button1. Свойству Text (пер. Текст) каждого редактора текста зададим пустую строку.
Изменим заголовок командной кнопки Button1. Для этого его свойству Caption зададим новое значение: ‘Вычислить’. После проведенных изменений основных свойств компонентов получим окно программы, приведенное на рис. 6.3.
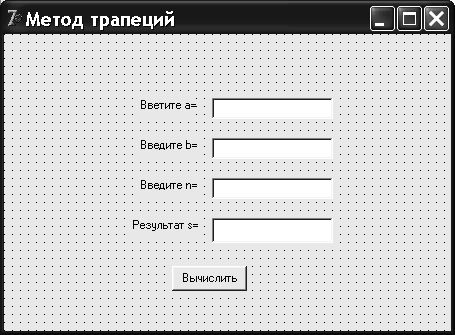
Рис. 6.3. Окно программы.
Заготовку процедуры-обработчика события OnClick командной кнопки ‘Вычислить’ создадим в такой последовательности: вначале выбираем кнопку “Вычислить” (щелчком левой клавиши), а затем дважды щелкаем левой клавишей мыши на ней.
2.4. Программирование вычислений определенных интегралов
Программирование численного интегрирования по формуле (6.4) проиллюстрируем на конкретных примерах. При этом описания типов переменных и операторы, реализующие необходимые вычисления, будем вводить посредствам клавиатуры в полученную заготовку процедуры-обработчика события OnClick.
Задание 1. Составить программу вычисления определенного интеграла
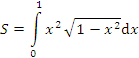
по формуле (6.4), приняв n=80.
Для улучшения ‘читабельности’ программы, имена переменным будем давать по обозначениям математических величин формулы (6.4). Тип переменных естественным образом определяется этой формулой. Поэтому между заголовком процедуры и операторной скобкой begin введем секцию var, в которой опишем типы переменных:
var
i,n:integer;
a,b,s,h,x:real;
В тело процедуры запишем операторы, реализующие:
1. Ввод исходных данных:
a:=StrToFloat(Edit1.Text);
b:=StrToFloat(Edit2.Text);
n:=StrToInt(Edit3.Text);
В операторах: StrToFloat(Edit1.Text) является стандартной функцией, преобразующей строковый тип поля Edit1 в вещественный тип; StrToInt(Edit3.Text) – стандартная функция, преобразующая строковый тип поля Edit3 в целый тип. Преобразованные значения присваиваются операторами 2-м вещественным переменным a, b и переменной целого типа n. Заметим, что в работающей программе вначале заполняются поля Edit1, Edit2, Edit3 текстами 0,0; 1,0; 80 соответственно, а затем производится ЩЛК на кнопке ‘Вычислить’.
2. Вычисление значений математических величин по формуле (6.4).
Для вычисления шага интегрирования h=(b – a)/n и полусуммы (y0+yn)/2 (см. формулу (6.4)) запишем операторы:
h:=(b-a)/n;
s:=(a*a*sqrt(1-a*a)+b*b*sqrt(1-b*b))/2.0;
Вычисление значения аргумента x1 определим записав оператор:
x:=a+h;
Вычисление частных сумм и окончательно полной суммы ординат (y0+yn)/2+y1+y2+…+yn-1 для соответствующих значений аргумента x1, x2,…,xn-1 зададим в цикле:
for i:=1 to n-1 do
begin
s:=s+x*x*sqrt(1-x*x);
x:=x+h;
end;
Следует понимать, что многократное выполнение оператора x:=x+h; приводит к тому, что переменная x последовательно будет принимать значения x1, x2,…,xn-1.
Умножив полученную сумму на h:
s:=h*s; ,
отобразим полученный результат в поле Edit4:
Edit4.Text:=FloatToStr(s);
В этом операторе, для преобразования вещественного значения переменной s в строковый тип, применяется стандартная функция FloatToStr(s).
По мере оформления окна, создания заготовки процедуры-обработчика события OnClick, ввода нами вышеприведенных описаний и операторов, система Delphi будет формировать модуль, окончательный текст которого может выглядеть так:
unit Unit1; // Заголовок модуля
interface // Начало интерфейсного раздела
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls,
Forms, Dialogs, StdCtrls;
type
TForm1 = class(TForm) // Начало описания класса
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Edit4: TEdit;
Button1: TButton;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end; // Конец описания класса
var
Form1: TForm1;
implementation // Начало раздела реализации
{$R *.dfm}
procedure TForm1.Button1Click(Sender: TObject); // Заголовок процедуры
var
i,n:integer;
a,b,s,h,x:real;
begin
a:=StrToFloat(Edit1.Text);
b:=StrToFloat(Edit2.Text);
n:=StrToInt(Edit3.Text);
h:=(b-a)/n;
s:=(a*a*sqrt(1-a*a)+b*b*sqrt(1-b*b))/2.0;