Файл: Исследование устойчивости методами Ляпунова Исследование устойчивости методом В. М. Попова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 112
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
y(t) Fasint A0 ( A cosnt B
sinnt),
(4.2.33)
n n
2 n1
где
A 2/
(asint)dt,
(4.2.34)

0 F
0
A 2/
(asint)cosntdt,
(4.2.35)

n F
0
B 2/
(asint)sinntdt.
(4.2.36)

n F
0
 у у
у уа у б
0 х 0 t
0
в х
a
Т=2/
Т
г


НЭ
W(p)
x(t)
–1
t
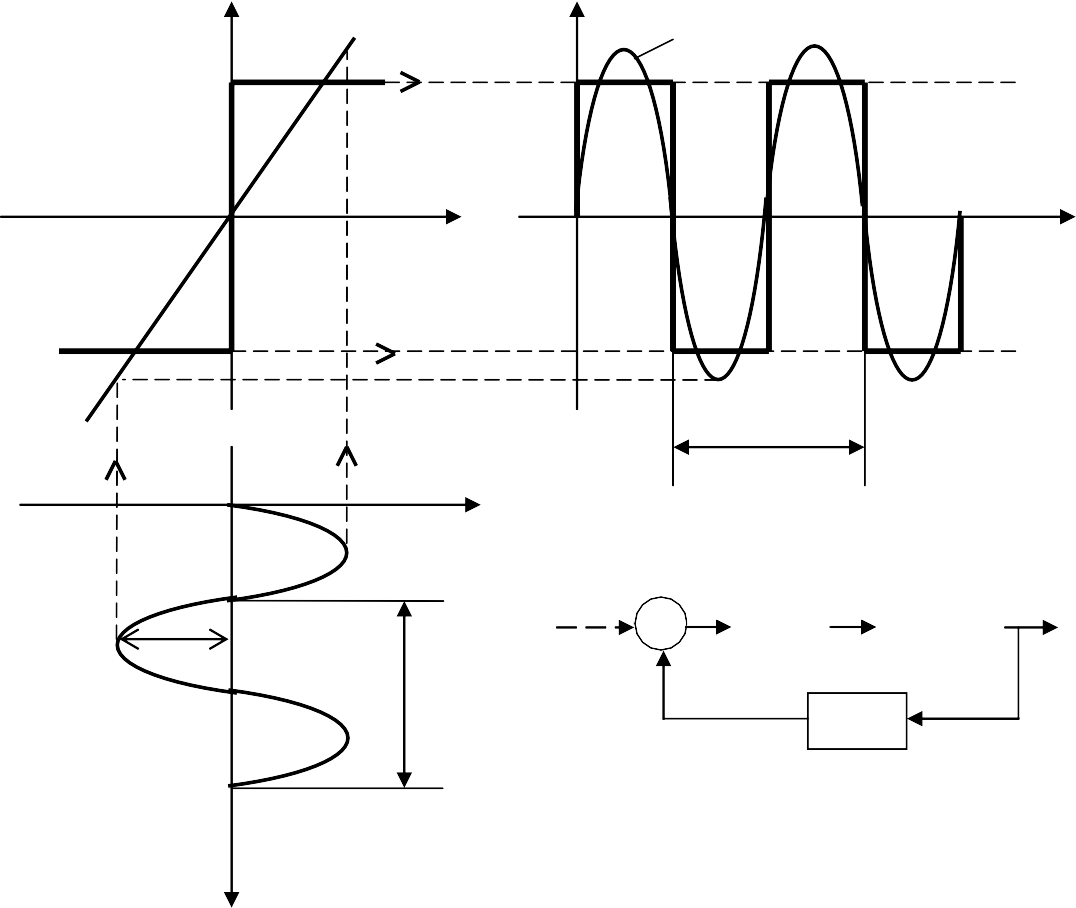
Рис. 4.2.7. Преобразование гармонического сигнала нелинейным элементом
В НЭ с однозначной симметричной нелинейностью относительно начала координат при синусоидальном входном сигнале в выходном периодическом сигнале отсутствуют постоянная составляющая и фа- зовое запаздывание. В НЭ с неоднозначной симметричной нелиней- ностью (например, типа люфт) в выходном сигнале также нет посто- янной составляющей, но имеется фазовое запаздывание. В НЭ с не- однозначной несимметричной нелинейностью (например, типа реле со смещением и петлей гистерезиса) в выходном сигнале имеются постоянная составляющая и фазовое запаздывание.
На основе свойства фильтра низких частот линейной части САУ считают, что на входе НЭ действуют только синусоидальные сигналы
первой гармоники, имеющие при симметричных автоколебаниях вид
x(t) ≈ asin ωt, (4.2.37)
а при несимметричных автоколебаниях – вид
x ≈ x0 + x* = x0 + asin ωt, (4.2.38) где x0 – постоянная составляющая.
Выходную величину НЭ можно определять графически, как на
рис. 4.2.7, либо аналитически – по формуле (4.2.33). При этом задача сводится к определению частоты ω и амплитуды а в случае симмет- ричных автоколебаний, либо частоты ω, амплитуды а и постоянной составляющей x0 в случае несимметричных автоколебаний.
При исследованиях нелинейных САУ в первом приближении в (4.2.33) учитывают только первую гармонику выходной величины НЭ
2
(4.2.39)
и нелинейное звено заменяют гармонически линеаризованным экви- валентным звеном с определенным коэффициентом передачи (рис. 4.2.7). При необходимости влияние высших гармоник на амплитуду и частоту первой гармоники выходной величины эквивалентного ли- нейного звена можно учитывать дополнительно [1].
При симметричных автоколебаниях на выходе НЭ нет постоян- ной составляющей А0=0 и коэффициенты отношения амплитуд пер- вых гармоник выходной и входной величин НЭ имеют вид
(4.2.40)
aa
Тогда выходная величина НЭ из (4.2.39) запишется в виде
y(t) q(a)asint q'(a)acost.
(4.2.41)
Поскольку входная величина НЭ x(t) связана соотношениями
asint x;
acost
px, p d
(4.2.42)
dt;
то из (4.2.41) связь выходной и входной величин НЭ имеет вид

q
y F(x) (a) q'(a) p x KH (q,q') x,
(4.2.43)
где, при ωt=ψ, согласно (4.2.40), (4.2.35), (4.2.36), получим значения
a
q' 1
2
F(asin)sin d,
0
2
F(asin)cos d.
(4.2.44)
(4.2.45)
a 0
Операция преобразования входной величины НЭ в его выходную величину в виде (4.2.43) называется гармонической линеаризацией не- линейности, а коэффициенты qи q′ называются коэффициентами гармонической линеаризации.
Гармонически линеаризованная передаточная функция НЭ на ос- новании (4.2.43) будет иметь вид
X ( p)
q(a) q'(a) p.
(4.2.46)
Амплитудно-фазовая характеристика гармонически линеаризо- ванного статического НЭ из (4.2.46) при p=jω получается в виде
WH (a)=q(a)+jq′(a), (4.2.47)
т.е. зависит только от амплитуды и не зависит от частоты сигнала на входе НЭ, в отличие от линейных звеньев.
Динамические нелинейности F(x, px), зависящие от скорости из- менения сигнала на входе НЭ, имеют коэффициенты qи q′, а значит и характеристики WH (jω), зависящие от его амплитуды а и частоты ω.
Существуют также нелинейности, для которых q, q′ и WH не зави- сят от амплитуды, а зависят только от частоты. Такие гармонически линеаризованные нелинейности называются псевдолинейными.
При несимметричных автоколебаниях на выходе НЭ в результате гармонической линеаризации при входном воздействии (4.2.38) вы- ходная величина НЭ представляются в виде
где
y F(x) F
0 (x0
, a) q(a, x0 )
q'(a, x0 )
p x*,
(4.2.48)
F0
2

1
F(x0 asin)d, 2 0
(4.2.49)
a
q' 1
2
F (x0 asin)sin d,
0
2
F(x0 asin)cos d,
(4.2.50)
(4.2.51)
a 0
x* asint.
Из (4.2.48) видно, что выходная величина НЭ содержит постоян- ную и периодическую составляющие, каждая из которых зависит от обоих составляющих входного сигнала x0 и а. Это является принци- пиальным отличием нелинейного звена от линейного и обусловлива- ет неприменимость принципа суперпозиции для НЭ (у линейных
звеньев по принципу суперпозиции каждая составляющая входа дает свою составляющую выхода).
При вычислении коэффициентов гармонической линеаризации по формулам (4.2.44), (4.2.45) нужно учитывать, что при симметричных нелинейностях интеграл от 0 до 2π можно заменить суммой двух ин- тегралов от 0 до π, а для симметричных относительно начала коорди- нат безгистерезисных нелинейностей при вычислении q(a) интеграл от 0 до 2π равен четырем интегралам от 0 до π/2 [2].
Для типовых нелинейностей расчетные формулы коэффициентов гармонической линеаризации приводятся в [2, 4, 10, 13] и др.
Пример 4.4. Вычислить коэффициенты гармонической линеаризации для НЭ с идеальной релейной характеристикой (рис. 4.2.6, а).
Данная нелинейность однозначна и симметрична

S
F(x) Ssign xS
при при
x 0;

.
x 0
(4.2.52)
При этом коэффициент q′(a)=0, а общий коэффициент гармонической ли-
неаризации KH (q,q′)=q(a) определяется только по формуле (4.2.44) в виде
q(a)
1 2
F(x)sin d
1

a
S sin d (S )(sin)d
a 0
0 0
(4.2.53)

0
2Ssind 2S(cos) (cos0) 2Scoscos0 4S,
где ψ=ωt.
a a
a a
Аналогично находятся выражения коэффициентов гармонической линеа- ризации для других нелинейностей. Например, для характеристики типа реле с зоной нечувствительности ± b(рис. 4.1.1, а)
KH (q,q') q(a) 4S
a
b 2


a
1 ,
q'(a) 0;
(4.2.54)
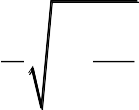
для нелинейности с насыщением при чи на линейном участке (рис. 4.1.1, в)
2k
a b S/ k, где k– коэффициент переда-

,
b b b2
KH(q,q') q(a)
arcsin 1
2

q'(a) 0;
(4.2.55)