Файл: Исследование устойчивости методами Ляпунова Исследование устойчивости методом В. М. Попова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 105
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
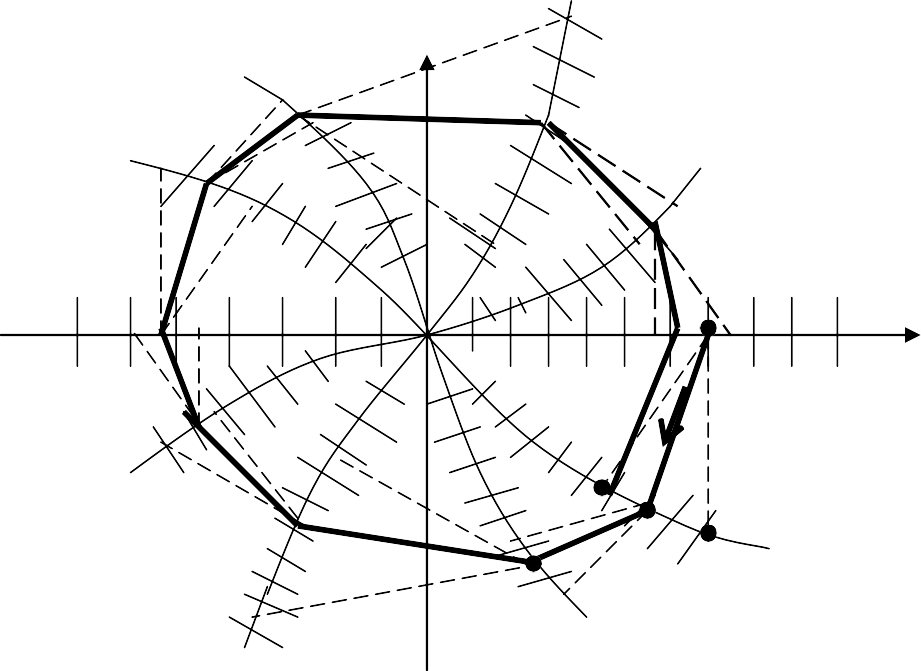
в любой точке которой фазовые траектории имеют одинаковый угол наклона dy/dx=c=сonst. Задавая различные значения c=const, рассчи- тывают по (4.2.18) и наносят на фазовую плоскость семейство изо- клин, на каждой из которых строят под углом tgα=c=const серию па- раллельных отрезков прямых, касательных к фазовым траекториям (рис. 4.2.3). На изоклине, совпадающей с осью абсцисс x, параллель- ные отрезки касательных направлены строго вертикально, что соот- ветствует нулевой скорости движения изображающих точек y=0.
Построение фазовой траектории (рис. 4.2.3) начинается из точки А, соответствующей начальным условиям, например x0=А; y0=0. То- гда, по указанным выше правилам, движение изображающей точки в нижней фазовой полуплоскости направлено влево. Из точки А, распо- ложенной на изоклине с5 (т. е. на оси x), проводим до пересечения с соседней изоклиной с4 две прямые: АВ параллельно отрезкам, нане- сенным на изоклину с5 (на ось x) и АС параллельно отрезкам, нане- сенным на изоклину с4. Поделив пополам отрезок ВС на изоклине с4, соединяем точку А с серединой отрезка ВС в точке D. Линия АDпри- мерно соответствует отрезку фазовой траектории. Аналогично стро- им отрезок фазовой траектории между изоклинами с4 и с3 и т. д.
Получаемая фазовая траектория (рис. 4.2.3) имеет вид сверты- вающейся спирали, следовательно, переходный процесс в системе колебательный затухающий. При других начальных условиях полу- чаются другие фазовые траектории, не пересекающиеся с построен- ными для данных начальных условий.
c3 c2c4
c1
c5=∞ A (x0=А, y0=0)
0 x
C
DB
Рис. 4.2.3. Построение фазовых траекторий методом изоклин
Фазовый портрет нелинейной САУ позволяет определить: 1) все возможные устойчивые и неустойчивые режимы работы САУ; 2) ус- тойчивость САУ и границы устойчивости; 3) автоколебания и их ам- плитуду; 4) тип переходных процессов (апериодический или колеба- тельный) и области начальных условий их возникновения; 5) пере- ходный процесс для любых начальных условий; 6) величину перере- гулирования при любом ступенчатом входном воздействии.
Удобство метода фазовых траекторий состоит в том, что вся со- вокупность переходных процессов в САУ при любых начальных ус- ловиях представляется в виде единого «фазового портрета» на фазо- вой плоскости. Недостатком является ограниченность анализа сис- темами второго порядка.
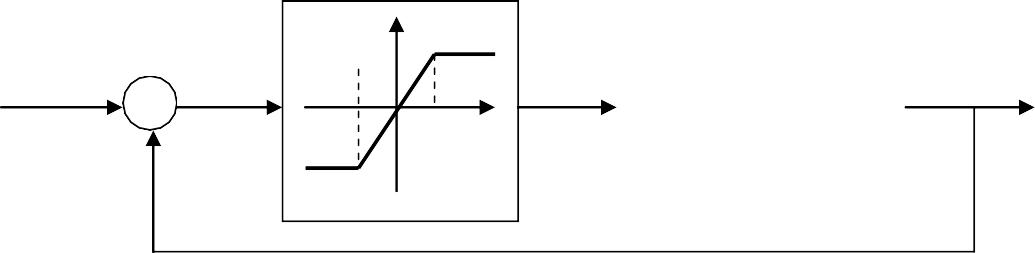
Пример 4.2. Исследовать методом фазовых траекторий процесс отработки ошибки управления в нелинейной следящей САУ с реальным усилителем с на- сыщением (с ограничением) (рис. 4.2.4).
–ε1
s
ε
K p(1+pT)
gε sx
–s ε1
-
Рис. 4.2.4. Нелинейная следящая система
ОФП замкнутой САУ по ошибке имеет вид
Ф ( p) (p) 1 p(1pT) ,
(4.2.19)
или
G( p) 1W( p) p(1 pT) KУK
(Tp2 p KУK)( p) (Tp2 p)G( p).
(4.2.20)
При исследовании свободного движения при G(p)=0 из (4.2.20) получаем дифференциальное уравнение переходного процесса при работе усилителя на линейном участке характеристики
d2 d
T K KУ 0,dt2 dt
(4.2.21)
которое определяет фазовые траектории САУ в линейной зоне при – ε1≤ ε ≤ ε1. При выходе усилителя за пределы линейной зоны его выходной сигнал бу-
дет иметь постоянное значение и дифференциальные уравнения переходного процесса из (4.2.20) запишутся в виде
d2 d
при ε ≥ ε1
T
dt2 dt KS;
(4.2.22)
d2 dпри ε ≤ – ε1
-
KS. dt2 dt
(4.2.23)
Обозначив ε=xи разделив уравнения (4.2.21), (4.2.22), (4.2.23) на dε/dt=dx/dt=y, получим дифференциальные уравнения фазовых траекторий для трех областей фазовой плоскости:
при – ε1< ε <+ε1 при ε ≥ +ε1
при ε ≤ –ε1
Tdy 1 KУKx;
dxy
Tdy 1 KS;dxy
Tdy 1 KS.dxy
(4.2.24)
(4.2.25)
(4.2.26)
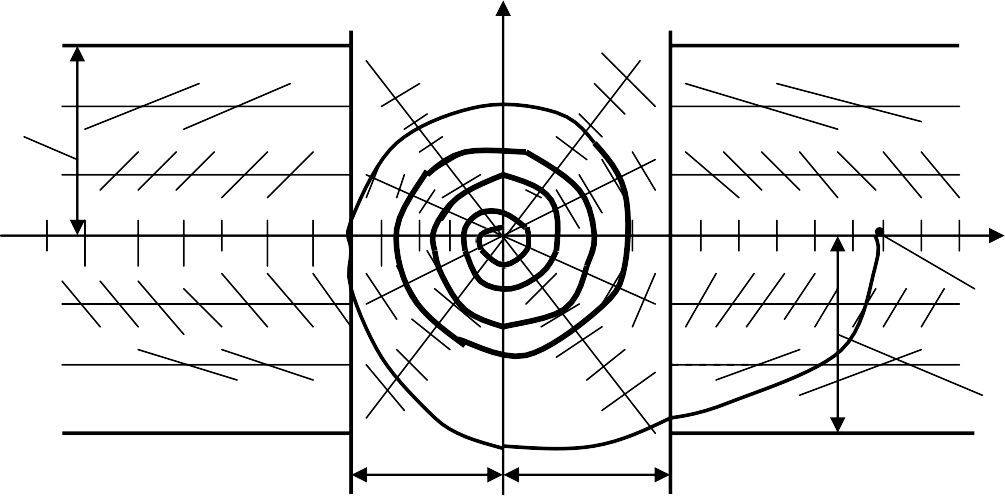
Фазовый портрет строим по методу изоклин (рис. 4.2.5). Вертикальные ли- нии переключения, которые разделяют фазовую плоскость на три области и на которых производится «сшивание» фазовых траекторий, проходят через значе- ния +x1=+ε1 и –x1=–ε1. Изоклины для линейной зоны на основании уравне- ния (4.2.24) представляются наклонными лучами, проходящими через начало координат и определяющимися уравнениями
yKУKx/(Tc1);
dy/dxctg.
(4.2.27)
Изоклины для правой нелинейной зоны при x>ε1 на основании (4.2.25) описываются уравнениями
yKS/(Tc1);
dy/dxctg.
(4.2.28)
Изоклины для левой нелинейной зоны при x < –ε1 на основании (4.2.26) описываются уравнениями
y KS/(Tc1);
dy/dxctg.
(4.2.29)
yKS
x
X0
–KS
–ε1 +ε1
Рис. 4.2.5. Фазовый портрет процессов в САУ
Из уравнений (4.2.28) и (4.2.29) следует, что изоклины в нелинейных зонах насыщения параллельны оси абсцисс, поскольку переменная xв этих уравнени- ях отсутствует, но фазовые траектории пересекают изоклины под разными уг- лами от 0 до 90º соответственно изменениям tgα=cот ∞ до 0. Изоклина, совпа- дающая с осью абсцисс, соответствует значениям c=∞, α=90º, а изоклины с с=0, α=0 на основании (4.2.28) и (4.2.29) проводятся на уровнях +KSи –KS.
Чем больше построено изоклин, тем точнее получается фазовый портрет для САУ. В примере приняты начальные условия y0=0, x0=X0, а параметры САУ – соответствующими затухающему колебательному процессу.
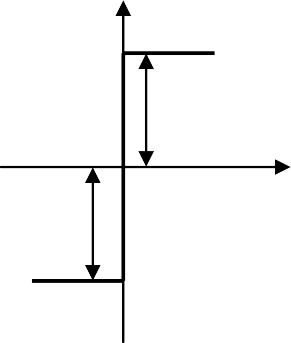
Пример 4.3. Исследовать процессы в САУ из примера 4.2 (рис. 4.2.4) при замене усилителя с насыщением на релейный регулятор с нелинейной релейной характеристикой S(ε)=S∙sign ε (рис. 4.2.6, а).
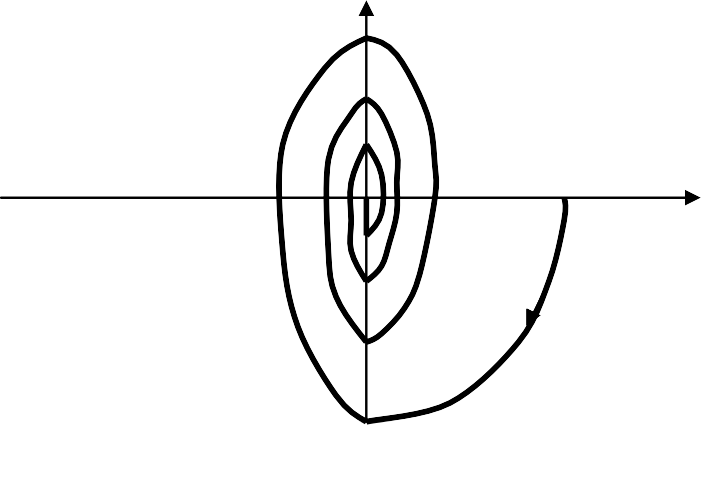S y=dx/dt+S X0
-S 0 ε
0 x=ε
а бРис. 4.2.6. Процессы в САУ с релейным регулятором
При этом свободное движение в САУ определяется уравнением
d2 d
T KSsign;dt2 dt
(4.2.30)
d2xdx
при ε=x>0
T
dt2 KS;
dt(4.2.31)
d2xdxпри ε=x<0
T
dt2-
KS. dt
(4.2.32)
Границей перехода от уравнения (4.2.31) к (4.2.32) является линия ε=x=0, т.е. ось ординат y, которая является также и линией переключения релейного регулятора. Уравнения изоклин в правой полуплоскости при ε=x>0 имеет вид (4.2.28), в левой при ε=x<0 вид (4.2.29).
Метод гармонической линеаризации (метод гармонического ба- ланса) относится к приближенным методом исследования нелиней- ных САУ любого порядка [1, 13, 15]. При этом для исследования не- линейных САУ используются частотные методы теории линейных САУ на основе гипотезы фильтра низких частот линейной части САУ и предположения о гармоническом характере свободных движений нелинейных САУ.
Сущность метода гармонической линеаризации (гармонического баланса) заключается в замене нелинейного элемента (НЭ) с характе- ристикой y=F(x, x) эквивалентным линейным звеном с коэффициен- том передачи КН (а, ω) (рис. 4.2.7, а), величина которого (угол накло- на на рис. 4.2.7, а) зависит от амплитуды а и частоты ω автоколеба- ний входной величины x(t) (рис. 4.2.7, в). В режиме автоколебаний в замкнутой CАУ условием эквивалентности такой замены служит ра- венство амплитуд и фаз выходного гармонического сигнала эквива- лентного линейного звена и первой гармоники выходного сигнала НЭ, которое называется гармоническим балансом. При этом предпо- лагается, что сигнал на входе НЭ является синусоидальным. Такое предположение справедливо, если линейная часть САУ имеет доста- точно большую инерционность и не пропускает высшие гармоники, т. е. обладает свойствами фильтра низких частот (рис. 4.2.7, г).
При подаче на вход НЭ сигнала x(t)=аsintна выходе НЭ поя- вится периодический сигнал y(t), форма которого будет зависеть от вида нелинейности y=F(x, x). Например, на выходе НЭ с нелинейно- стью типа «идеальное реле» образуется периодический сигнал пря- моугольной формы (рис. 4.2.7, б). В общем случае несинусоидальный периодический сигнал на выходе НЭ можно разложить в ряд Фурье