Файл: 1. Свет. Интерференция света. Условие максимума и минимума интерференции.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 237
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Интерференция света в тонких пленках или полосы ровного наклона.
6.Дифракция Френеля на круглом отверстии и диске.
7.Дифракция Фраунгофера на прямоугольной щели.
8. Дисперсия и разрешающая сила спектрального прибора.
Оптическая активность веществ. @
Поляризация света при отражении и преломлениина границе раздела
двух диэлектрических сред. Закон Брюстера.
4. 3. Поляризация света при двойном лучепреломлении.
6. 1. Характеристики теплового излучения. @
Волновая функция, её статистический смысл. Задание состояния микрочастицы.
28. Состав ядра. Характеристики ядра. Размеры ядер.
Поляризация света при отражении и преломлениина границе раздела
двух диэлектрических сред. Закон Брюстера.
Действие поляризаторов может быть основано на поляризации света при отражении и преломлении на границе раздела двух диэлектриков.
Оптически изотропная среда (т.е. среда, имеющая одинаковые оптические свойства во всех направлениях) представляет собой систему электрических зарядов – ионов и электронов, способных совершать вынужденные колебания под действием электромагнитных волн. Частота колебаний, соответствующая диапазону частот видимого света очень большая (порядка 1015 Гц). Поэтому только заряженные частицы очень маленькой массы могут следовать за изменением поля световой волны. Такими частицами являются электроны. Атомы и их ядра не могут следовать за изменением этого поля в силу их большой инертной массы. При этом предполагается, что в веществе электроны связаны квазиупругими силами, т.е. являются колебательными системами, характеризующимися частотой собственных колебаний.
П
 ростейшей системой, излучающей электромагнитные волны, является колеблющийся электрический диполь (рис. 4.4 а). Под действием электромагнитной волны электроны вещества совершают вынужденные колебания, излучая вторичные электромагнитные волны той же частоты, что и частота падающего света. Если волна распространяется в изотропной среде, то волновой фронт будет сферическим (рис. 4.4 б). При этом интенсивность вторичных волн зависит от угла θ и поэтому различна в разных направлениях. Зависимость интенсивности от угла наглядно показано на диаграмме направленности диполя (рис. 4.4 в). На рис. 4.4.в видно, что в направлении линии АА' (оси осциллятора) происходит колебания электрона, поэтому интенсивность излучения в этом направлении отсутствует. Интенсивность излучения будет максимальна в направлении оси Х, перпендикулярном линии АА'.
ростейшей системой, излучающей электромагнитные волны, является колеблющийся электрический диполь (рис. 4.4 а). Под действием электромагнитной волны электроны вещества совершают вынужденные колебания, излучая вторичные электромагнитные волны той же частоты, что и частота падающего света. Если волна распространяется в изотропной среде, то волновой фронт будет сферическим (рис. 4.4 б). При этом интенсивность вторичных волн зависит от угла θ и поэтому различна в разных направлениях. Зависимость интенсивности от угла наглядно показано на диаграмме направленности диполя (рис. 4.4 в). На рис. 4.4.в видно, что в направлении линии АА' (оси осциллятора) происходит колебания электрона, поэтому интенсивность излучения в этом направлении отсутствует. Интенсивность излучения будет максимальна в направлении оси Х, перпендикулярном линии АА'.В
 заимодействие электронной оболочки атомов с электромагнитным полем световой волны приводит к их возбуждению. Возбужденные атомы, приходя в нормальное (невозбужденное) состояние, излучают вторичные электромагнитные волны. Поскольку среднее расстояние между атомами в жидкостях и твердых телах мало по сравнению с длиной цуга волн (около 3м), то электронные оболочки большого числа атомов возбуждаются одним цугом волн. Поэтому вторичные волны оказываются когерентными как между собой, так и падающей световой волной. Эти волны взаимно интерферируют. Их интерференцией объясняются явления отражения и преломления света в веществе.
заимодействие электронной оболочки атомов с электромагнитным полем световой волны приводит к их возбуждению. Возбужденные атомы, приходя в нормальное (невозбужденное) состояние, излучают вторичные электромагнитные волны. Поскольку среднее расстояние между атомами в жидкостях и твердых телах мало по сравнению с длиной цуга волн (около 3м), то электронные оболочки большого числа атомов возбуждаются одним цугом волн. Поэтому вторичные волны оказываются когерентными как между собой, так и падающей световой волной. Эти волны взаимно интерферируют. Их интерференцией объясняются явления отражения и преломления света в веществе.
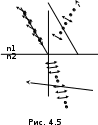
При падении естественного света на границу раздела двух диэлектриков (например, из воздух на стекло) часть его отражается, а часть преломляется (рис. 4.5). Отраженный и преломленный свет оказываются частично поляризоваными. В отраженном свете преобладают волны, у которых световой вектор Е колеблется в плоскости, перпендикулярной плоскости падения (на рис. 4.5 колебания вектора Е изображены точками), а в преломленном свете – в плоскости падения (на рис. 4.5 колебания вектора Е изображены стрелками).
Степень поляризации как отраженного, так и преломленного света зависит от угла падения лучей и показателей преломления сред. Шотландский физик Дэвид Брюстер исследуя поляризацию света, установил (1815 г.) связь между относительным показателем преломления диэлектрика и углом падения света, при котором отраженный от поверхности свет полностью поляризован. Согласно закону Брюстера при угле падения iБ (угол Брюстера), определяемого соотношением
t
 g iБ = n21
g iБ = n21отраженный луч будет полностью плоскополяризован а преломленный луч – частично с максимальной степенью поляризации (рис. 4.6). Если свет падает на границу раздела под углом Брюстера, то отраженный и преломленный лучи взаимно перпендикулярны (это условие вытекает из закона Брюстера).
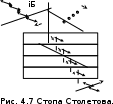
Степень поляризации преломленного света можно значительно повысить, пропуская свет через устройство, называемое стопой Столетова (рис. 4.7). Стопа Столетова представляет собой совокупность одинаковых параллельных друг другу пластинок из прозрачного диэлектрика (например, стекла). При многократном отражении и преломлении на каждой границе степень поляризации вырастает и на выходе из стопы свет становится полностью поляризованным.
З
 акон Брюстера можно пояснить, основываясь на диаграмме направл
акон Брюстера можно пояснить, основываясь на диаграмме направл енности излучения электрического диполя (осциллятора). Представим падающий естественный свет как результат сложения двух взаимно перпендикулярных колебаний (рис. 4.8). Один световой вектор (обозначим его
енности излучения электрического диполя (осциллятора). Представим падающий естественный свет как результат сложения двух взаимно перпендикулярных колебаний (рис. 4.8). Один световой вектор (обозначим его
Е||) будет колебаться в плоскости падения (на рис. 4.8 вектор Е|| показан стрелками), а другой (обозначим его Е) будет колебаться в плоскости, перпендикулярной плоскости падения (на рис. 4.8 вектор Е показан точками).
При прохождении света через вещество под действием вектора Е|| электроны вещества будут совершать вынужденные колебания в плоскости падения (эти осцилляторы, оси которых лежат в плоскости падения, на преломленном луче обозначены стрелками), излучая при этом вторичные сферические волны в плоскости падения. Интенсивность таких волн будет максимальна в перпендикулярном направлении (это показано диаграммой направленности диполя на преломленном луче). Световому вектору Е будут соответствовать осцилляторы, оси которых лежат в перпендикулярной плоскости (на преломленном луче они обозначены точками). В направлении колебаний электронов излучения вторичных волн не происходит. При угле падения i= iБ отраженный луч перпендикулярен преломленному лучу и, следовательно, параллелен осцилляторам, оси которых расположены в плоскости падения. Данные осцилляторы не излучают в направлении отраженного луча и вклад в отраженную волну не дают. Отсюда следует, что в отраженном луче будет присутствовать только колебания Е и отраженный луч будет полностью поляризован.
Эффект поляризации отраженного света используется, например, для обнаружения с воздуха пленок нефти на поверхности моря.
4. 3. Поляризация света при двойном лучепреломлении.
Действие ряда поляризаторов основано на поляризации света при прохождении его через оптически анизотропные среды (т.е. среды, имеющие различные оптические свойства в различных направлениях). Все прозрачные кристаллы оптически анизотропны. Исключением являются кристаллы, имеющие кубическую кристаллическую решетку (например, соль NaCl). При прохождении света через оптически анизотропные кристаллы наблюдается явление двойного лучепреломления, которое состоит в том, что упавший на кристалл луч разделяется внутри кристалла на два луча, распространяющиеся с различными скоростями и в различных направлениях. Это явление впервые было обнаружено датским ученым Э. Бартолином в 1669 г. для исландского шпата.
В зависимости от типа симметрии оптически анизотропные кристаллы бывают одноосные либо двуосные, т.е. имеют одну или две оптические оси. Оптической осью называется такое направление в кристалле, вдоль которого распространяющийся свет не испытывает двойного лучепреломления. Важно отметить, что любая прямая параллельная данному направлению, также является оптической осью кристалла. Примером одноосного кристалла (рис. 4.9) является исландский шпат (диагональ кристалла ОО' совпадает с оптической осью), а также кварц, турмалин, апатит и другие. К двуосным кристаллам относятся гипс, слюда, топаз.
В
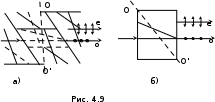 одноосных кристаллах (рис. 4.9 а) один из преломленных лучей, образующихся при двойном лучепреломлении, лежит в плоскости падения и подчиняется закону преломления, поэтому его назвали обыкновенным лучом и обозначают буквой "о". Скорость обыкновенного луча υо численно одинакова по всем направлениям: υо = c/nо, где nо = const- показатель преломления кристалла для обыкновенного луча. Второй луч называют необыкновенным и обозначают буквой "е". Он не лежит в плоскости падения и не подчиняется закону преломления. Соответственно скорость необыкновенного луча υе = c/nе, где nе - показатель преломления кристалла для необыкновенного луча. Значения nе и υе зависят от направления распространения необыкновенного луча по отношению к оптической оси кристалла. Для луча, распространяющегося вдоль оптической оси показатели преломления обыкновенного и необыкновенного лучей равны
одноосных кристаллах (рис. 4.9 а) один из преломленных лучей, образующихся при двойном лучепреломлении, лежит в плоскости падения и подчиняется закону преломления, поэтому его назвали обыкновенным лучом и обозначают буквой "о". Скорость обыкновенного луча υо численно одинакова по всем направлениям: υо = c/nо, где nо = const- показатель преломления кристалла для обыкновенного луча. Второй луч называют необыкновенным и обозначают буквой "е". Он не лежит в плоскости падения и не подчиняется закону преломления. Соответственно скорость необыкновенного луча υе = c/nе, где nе - показатель преломления кристалла для необыкновенного луча. Значения nе и υе зависят от направления распространения необыкновенного луча по отношению к оптической оси кристалла. Для луча, распространяющегося вдоль оптической оси показатели преломления обыкновенного и необыкновенного лучей равны
nе = nо и υе = υо. Значение nе наиболее сильно отличается от nо для направления, перпендикулярного оптической оси. Все эти различия между обыкновенным и необыкновенным лучами имеют место только внутри кристалла. На выходе из кристалла оба луча распространяются с одинаковой скоростью. В двуосных кристаллах оба преломленных луча ведут себя как необыкновенные.
Исследование обыкновенного и необыкновенного лучей показывает, что оба луча на выходе из кристалла полностью поляризованы. Вектор Е обыкновенного луча колеблется перпендикулярно главной плоскости (на рис. 4.9 эти колебания обозначены точками), а вектор Е необыкновенного луча колеблется в главной плоскости (на рис. 4.9 эти колебания показаны стрелками). Главной плоскостью или главным сечением одноосного кристалла называется плоскость, проходящая через падающий луч и пересекающую его оптическую ось (рис. 4.9 б).
Двойное лучепреломление объясняется тем, что в кристаллах диэлектрическая проницаемость ε оказывается зависящей от направления. Для одноосных кристаллов диэлектрическая проницаемость в направлении оптической оси и диэлектрическая проницаемость в направлении, перпендикулярном к ней, имеют различные значения. Поскольку абсолютный показатель преломления
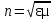 , а для большинства кристаллов магнитная проницаемость µ ≈ 1, то
, а для большинства кристаллов магнитная проницаемость µ ≈ 1, то 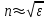 . Следовательно, из анизотропии диэлектрической проницаемости εвытекает анизотропия показателя преломления n.
. Следовательно, из анизотропии диэлектрической проницаемости εвытекает анизотропия показателя преломления n.Допустим, что в точке S (рис. 4.10) внутри одноосного кристалла находится точечный источник света. На рис. 4.10 показано распространение обыкновенного и необыкновенного лучей в кристалле. Главная плоскость совпадает с плоскостью чертежа, прямая ОО' – оптическая ось. Волновая поверхность обыкновенного луча является сферой (т.к. nо = const и υо = c/nо = =const), необыкновенного луча – эллипсоид вращения (т.к.
nе ≠ const и υе = c/nо ≠ const). На рис. 4.10 хорошо видно, что наибольшее расхождение волновых поверхностных обыкновенного и необыкновенного