Файл: Учебное пособие Рыбинск 2007 удк 681. 5 Павлов Р. В. Основы теории управления. Учебное пособиергата. Рыбинск, 2007. 83 с.doc

. В зависимости от параметров ДУ возможно несколько случаев. Некоторые из них представлены на рис. 76.

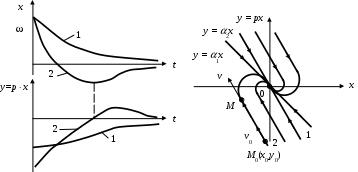
Рис. 76,а соответствует комплексным корням с отрицательной вещественной частью (наличие затухающего переходного процесса), случай рис. 76,б показывает фазовую траекторию апериодического затухающего процесса при отрицательных вещественных корнях характеристического уравнения.

ДУ представляют собой выражения для проекций скорости изображающей точки М на óси координат. Поэтому по значениям правых частей уравнений в каждый момент времени можно судить о движении точки М, и, следовательно, о поведении реальной НСАУ в процессе управления.

Фазовая траектория – это качественная характеристика НСАУ. Для определения количественных значений выходных сигналов необходимо решать дифференциальные уравнения в каждой точке.

Если дифференциальные уравнения составлены для отклонений выходного сигнала от установившихся значений, то для устойчивой системы фазовая кривая будет стремиться в начало координат.



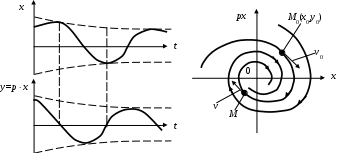
а )

б)

Рис. 76. Примеры фазовых траекторий

13.3. Устойчивость по Ляпунову

Для нелинейных систем существует понятие устойчивости по Ляпунову. Невозмущенное движение (установившийся процесс) называется устойчивым, если при заданной сколь угодно малой области  можно найти такую область , что при начальных условиях, расположенных внутри этой области, переходный процесс будет таким, что изображающая точка не выйдет из области  при любом сколь угодно большом значении времени t (рис. 77).

Аналитически условие можно представить в следующем виде.

При начальных условиях решение ДУ переходного процесса удовлетворяет неравенствам при любом сколь угодно большом t, начиная с некоторого t = T > 0.



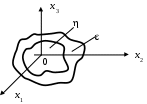
Рис. 77. Устойчивость по Ляпунову

13.4. Гармоническая линеаризация

Данный метод используется для приближенного определения наличия автоколебаний и устойчивости нелинейных систем любого порядка.

Пусть дано некоторое нелинейное выражение вида

---

и задано ; . Тогда .

Разложим функцию F в ряд Фурье:



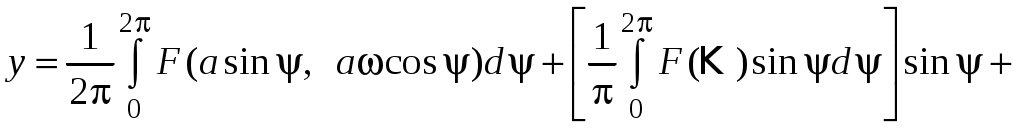
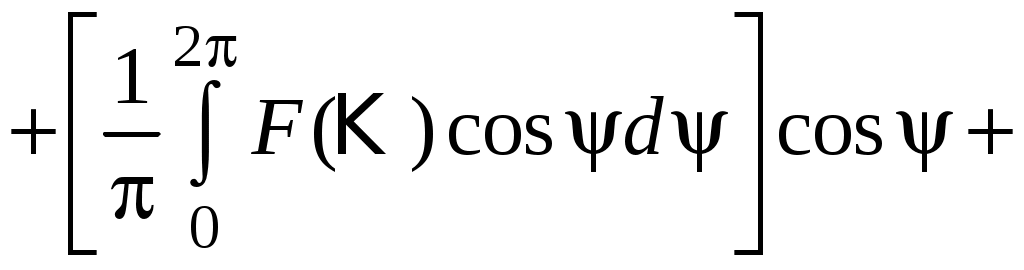высшие гармоники.

Предположим, что первое слагаемое равно нулю, т. е. в разложении нет постоянной составляющей.

Если принять во внимание, что из исходных выражений следует и , то можно получить

+ высшие гармоники,

где q и q – коэффициенты гармонической линеаризации.

;

.

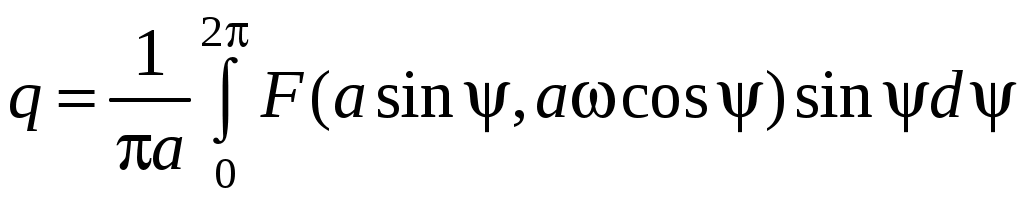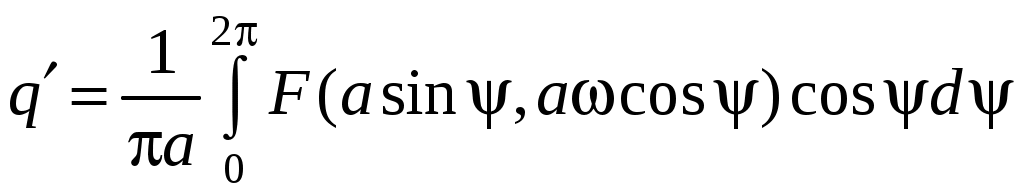Таким образом, исходное уравнение при х = аsint с точностью до высших гармоник аналогично линейному. В этом и заключается метод гармонической линеаризации.

Если значения амплитуды a и частоты  постоянны (периодический процесс), то и коэффициенты q и q постоянны. В переходном процессе амплитуда и частота непостоянны. В этом и заключается отличие данного метода от обычных методов линеаризации. Это отличие позволяет при анализе систем обнаружить особенности работы НСАУ.

Рассмотрим простой частный случай y = F(x).

Если эта кривая не имеет гистерезисной петли, то q = 0. Тогда + высшие гармоники;

Таким образом, криволинейная характеристика заменяется прямой линией, тангенс угла которой зависит от амплитуды входного сигнала.

Найдем гармонически линеаризованное уравнение для замкнутой нелинейной системы в целом. Линейная часть описывается ДУ следующего вида любой сложности:

.

Нелинейная часть описана простым соотношением:

---

.

После линеаризации уравнение нелинейного звена будет иметь вид:

.

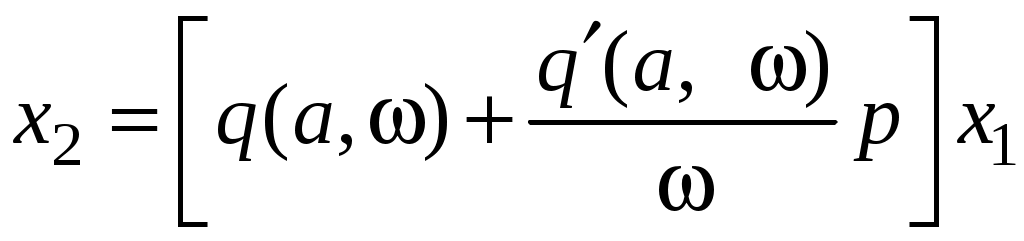Уравнение не имеет высших гармоник. Объясняется это следующим. Как правило, в замкнутой САУ линейная часть обладает свойствами низкочастотного фильтра. Это легко обнаружить при рассмотрении ЛАЧХ линейной замкнутой САУ.

Общее характеристическое уравнение замкнутой НСАУ имеет вид:

.

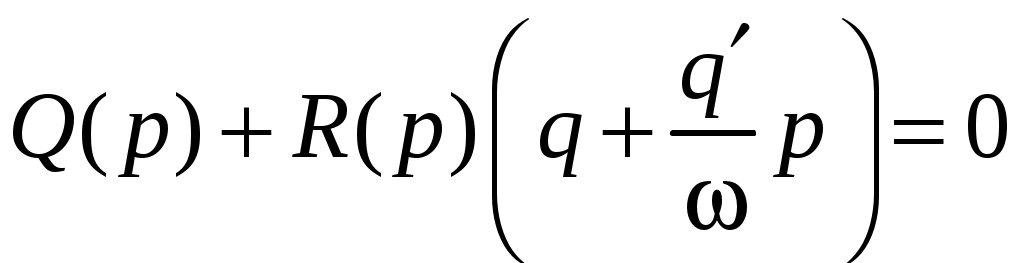Если в системе имеют место автоколебания, т. е. имеются незатухающие колебания с амплитудой а_П и частотой _П, то коэффициенты этого уравнения становятся постоянными. С другой стороны, из теории линейных САУ следует, что имеет место пара чисто мнимых корней характеристического уравнения. Поэтому, чтобы определить автоколебания нелинейных САУ, можно найти границу устойчивости соответствующей линейной САУ, т. е. можно воспользоваться критериями устойчивости линейной САУ (алгебраическими и частотными).

Заключение

В пособии были рассмотрены вопросы проектирования систем автоматического управления.

Особое внимание было уделено вопросам анализа и синтеза непрерывных линейных САУ. Кратко представлен раздел нелинейных систем. Представленный материал дает теоретическую базу для исследования дискретных и цифровых систем управления, изучение которых выходит за рамки данного курса.

ЛИТЕРАТУРА

1.Бесекерский В. А., Попов Е. П. Теория систем автоматического регулирования. – М.: изд. Наука, гл. ред. физ-мат. лит. – 1975, 768 с.

2.Сборник задач по теории автоматического регулирования и управления, под ред. В. А. Бесекерского. – М.: гл. ред. физ-мат. лит. – 1972, 588 с.

3. Попов Е. П. Теория линейных систем автоматического регулирования и управления. Учебное пособие – М.: Наука, 1989.

4. Солодовников В. В., Плотников В. Н., Яковлев А. В. Основы теории и элементы систем автоматического регулирования. Учебное пособие. – М.: Машиностроение, 1985.

5. Теория автоматического управления /Под ред. А. А.Воронова – М.: Высшая школа, 1987.

---