Файл: Учебное пособие Рыбинск 2007 удк 681. 5 Павлов Р. В. Основы теории управления. Учебное пособиергата. Рыбинск, 2007. 83 с.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 264
Скачиваний: 2
СОДЕРЖАНИЕ
1. Основные понятия и определения
3. Дифференциальные уравнения ипередаточные функции
5. Типовые звенья САУ и их характеристики
6. Построение передаточных функций САУ
7. Составление исходных дифференциальныхуравнений САУ
9. Процесс управления и требования к нему
9.1. Оценка устойчивости линейной САУ
9.3. Качество переходного процесса
10.2. Типы корректирующих устройств
10.3. Пример синтеза последовательного корректирующего устройства
10.4. Пример синтеза параллельного корректирующего устройства
11.3. Определение передаточных функций элементов системы
11.4. Построение структурной схемы системы
11.5. Построение логарифмических частотных характеристик разомкнутой системы
11.6. Определение устойчивости и запасаустойчивости по амплитуде и фазе
11.7. Определение критического значения добротностис помощью критерия Гурвица
11.8. Введение скоростной обратной связи
11.9. Нахождение минимального коэффициентаскоростной обратной связи
11.10 Определение оптимального коэффициентаскоростной обратной связи
12.2. Характеристики случайных величин и процессов
12.3. Прохождение случайного сигнала через линейную непрерывную систему
12.4. Расчет установившейся ошибки САУ
12.5. Расчеты по минимуму ошибки
13.1. Общий метод составления уравнений нелинейных САУ
13.3. Устойчивость по Ляпунову
10.3. Пример синтеза последовательного
корректирующего устройства
Его удобно выполнять по логарифмическим характеристикам.
Последовательность действий следующая.
-
Строятся логарифмические характеристики исходной системы L0() и 0(). -
На основе анализа ЛАЧХ и ЛФЧХ (например, анализируется устойчивость САУ) строится желаемая ЛАЧХ LЖ(). -
Находится геометрическая разность имеющихся графиков и получается характеристика корректирующего звенаLК(). -
ЛАЧХ корректирующего звена аппроксимируется. -
Выводится формула передаточной функции корректирующего устройства.
Данный алгоритм поясняется на рис. 56.
Желательно, чтобы ЛАЧХ на частоте среза имела наклон –20 дБ/дек или –40 дБ/дек для обеспечения качества переходного процесса и устойчивости.
Аппроксимацию в данном примере делать не надо, т. к. наклоны характеристики стандартные.
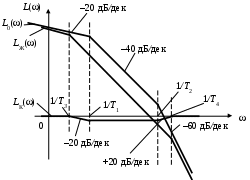
Рис. 56. Пример синтеза последовательного корректирующего устройства
Передаточная функция имеет вид:
 .
.10.4. Пример синтеза параллельного
корректирующего устройства
Структурная схема САУ имеет вид (рис. 57).
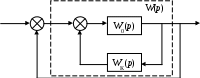
Рис. 57. Коррекция в виде местной обратной связи
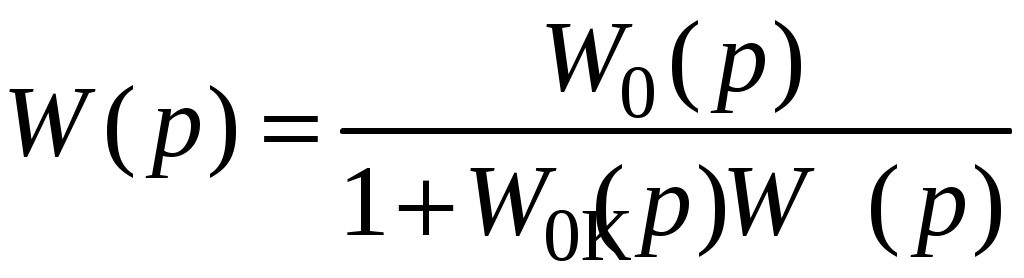 .
.Если считать, что
 ,
,или для ЛАЧХ
В результате получается следующая последовательность действий.
-
Строятся логарифмические характеристики исходной системы, L0() и 0(). -
Из заданных критериев качества строится желаемая характеристика LЖ(). -
Определяется интервал частот, в котором выполняется условие W0(p)WК(p) >> 1. -
Находится логарифмическая характеристика корректирующего устройстваLК().
5. ЛАЧХ корректирующего звена аппроксимируется.
6. Определяется передаточная функцияWК(p).
Графические зависимости представлены на рис. 58.
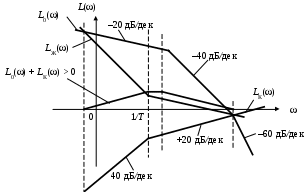
Рис. 58. Пример синтеза параллельного корректирующего устройства
Передаточная функция корректирующего устройства следующая
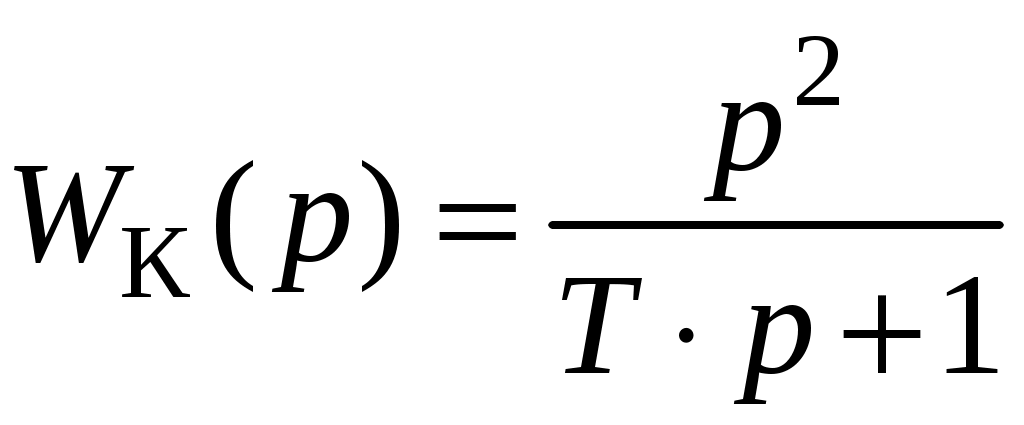 .
.11. пример разработки сау
11.1. Задание
Необходимо выполнить следующие действия.
-
Описать работу системы. -
Определить передаточные функции элементов системы. -
Составить структурную схему системы. -
Построить логарифмические характеристики разомкнутой
системы. -
Определить устойчивость и запас устойчивости по амплитуде и фазе. -
С помощью критерия Гурвица определить критическое значение добротности системы без обратной связи. -
Ввести скоростную обратную связь. -
Найти минимальное значение коэффициента скоростной обратной связи, необходимого для устойчивости системы. -
Найти оптимальное значение коэффициента скоростной обратной связи, необходимого для обеспечения показателей качества переходного процесса системы.
Исходная схема САУ (рис. 59):
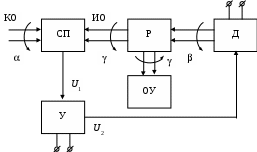
Рис. 59. Исходная схема системы
где СП – сельсинная пара;
Р – редуктор;
Д – двигатель;
ОУ – объект управления;
У – усилитель;
КО – командная ось;
ИО – исполнительная ось;
α – угол поворота сельсин-датчика – это командное воздействие;
β – угол поворота двигателя;
γ – угол поворота редуктора – это исполнительное воздействие;
U1 – выходной сигнал СП;
U2 – выходной сигнал У;
Параметры САУ:
UMAX – максимальное напряжение на выходе сельсин-трансформатора;
kУ – коэффициент усиления У;
TУ – постоянная времени У;
UУ – номинальное напряжение на обмотке управления двигателя;
NXX – число оборотов в минуту при холостом ходе двигателя и при номинальном напряжении двигателя;
TД – постоянная времени Д;
i – передаточное число редуктора;
SТГ – крутизна выходной характеристики тахогенератора;
tРЕГ – время регулирования;
– величина перерегулирования;
n – число полных колебаний выходного сигнала.
Исходные данные:
kУ = 900;
TУ = 0.01 с;
TД = 0.052 с;
i = 1.2 103;
UMAX = 5 В;
UУ = 30 В;
NXX = 10000 об/мин;
SТГ = 0.001 В с/рад;
tРЕГ 1 с;
30%;
n = 1,5.
11.2. Описание работы системы
Из схемы системы, приведённой в задании видно (см. рис. 59), что задающим устройством является командная ось, вращаемая сельсин-датчиком по произвольному закону α = α(t). Тот же самый закон угла поворота во времени α(t) = γ(t) должен быть автоматически воспроизведён на выходе системы, т. е. на объект управления и на исполнительную ось. Если углы поворота командной и исполнительной оси не равны, (α(t) γ(t)), то на выходе сельсинной пары возникает напряжение рассогласования U1. Величина U1 зависит от величины углов поворота командной и исполнительной осей. Напряжение U1 поступает на вход усилителя, на выходе которого возникает напряжение U2, поступающее на обмотку управления двигателя. В результате этого начинает вращаться ротор двигателя в сторону уменьшения ошибки рассогласования (θ = α – γ) до согласования двух осей. То есть поворот ротора двигателя через редуктор задаёт новый закон угла поворота исполнительной оси. Ротор двигателя будет вращаться до тех пор, пока ошибка рассогласования не будет сведена к нулю, после чего он остановится. Таким образом, система охвачена отрицательной обратной связью.
11.3. Определение передаточных функций элементов системы
Для нахождения передаточных функций элементов системы, приведенной в задании, определим сначала их дифференциальные уравнения. Дифференциальные уравнения составляем на основе принципа действия.
1. Сельсинная пара
Сельсинную пару можно с достаточной для практики точностью считать безынерционной. Поэтому её дифференциальное уравнение имеет вид:
где
Передаточная функция СП имеет вид:
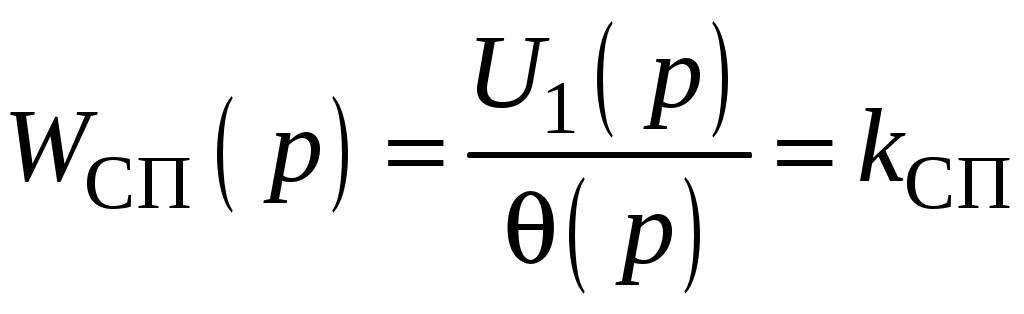
;
2. Усилитель
Усилитель – апериодическое звено первого порядка, поэтому его дифференциальное уравнение имеет вид:
где
Передаточная функция усилителя имеет вид:
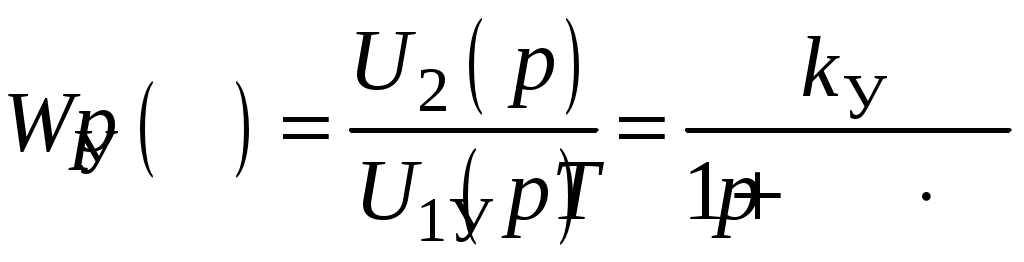 ;
;TУ = 0,01 с;
3. Двигатель.
Двигатель – интегрирующее звено с замедлением, т. к. в качестве выходной величины двигателя рассматривается угол поворота, а не угловая скорость. Угол поворота является интегралом от угловой скорости.
Данное звено описывается следующим дифференциальным уравнением
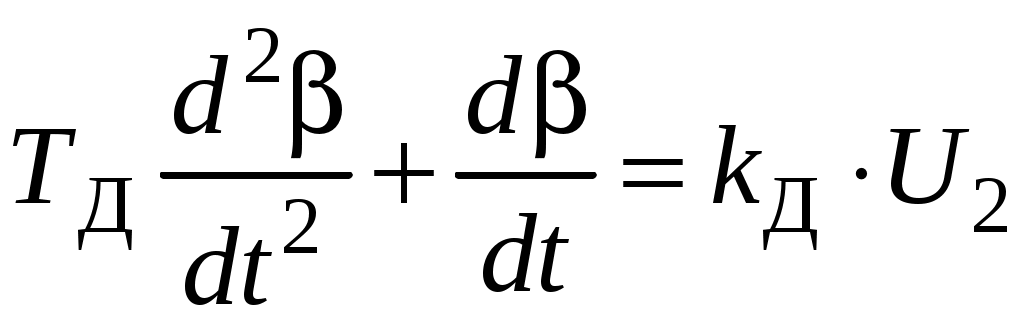 ;
;Передаточная функция звена имеет вид:
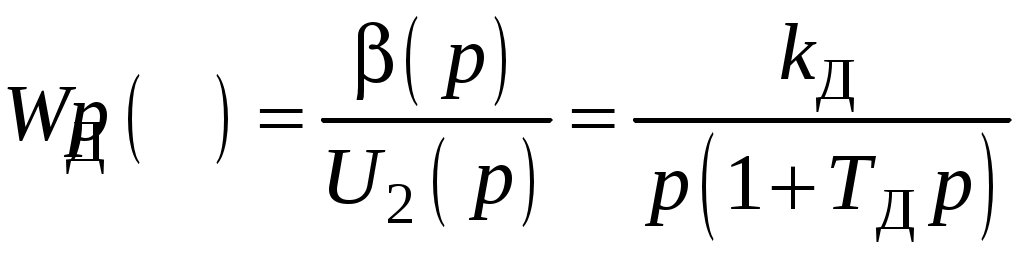 ,
,где
Определим
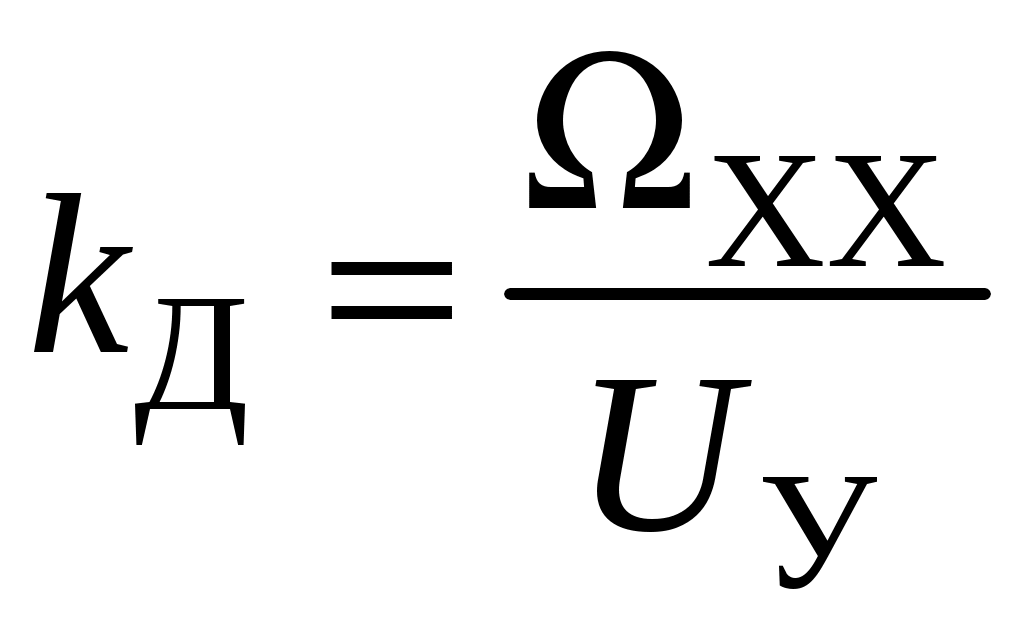 ,
,где