Файл: Учебное пособие Рыбинск 2007 удк 681. 5 Павлов Р. В. Основы теории управления. Учебное пособиергата. Рыбинск, 2007. 83 с.doc

.

Тогда имеем

; .

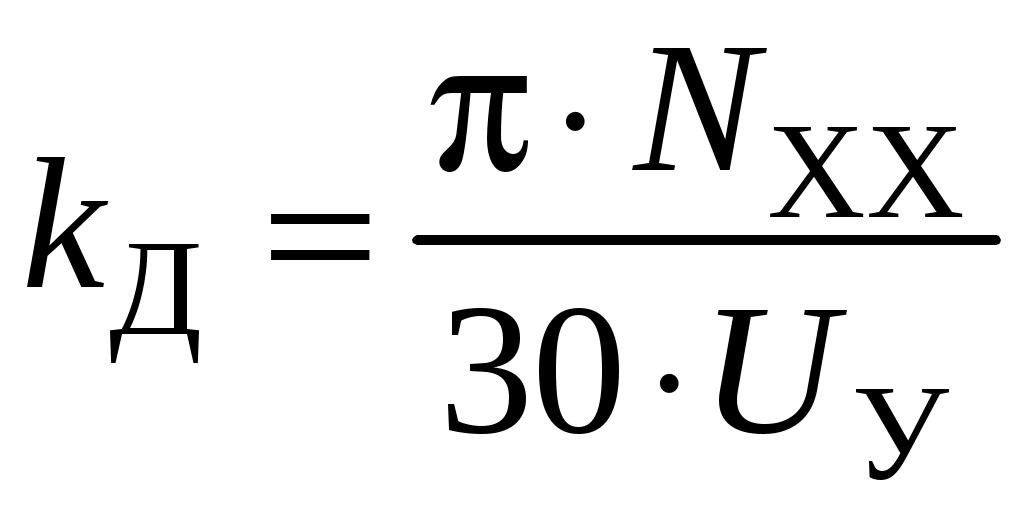4. Редуктор

Редуктор – безынерционное звено, поэтому оно описывается следующим дифференциальным уравнением:

,

где – коэффициент передачи редуктора.

Передаточная функция редуктора

.

определим по следующей формуле:

, .

---

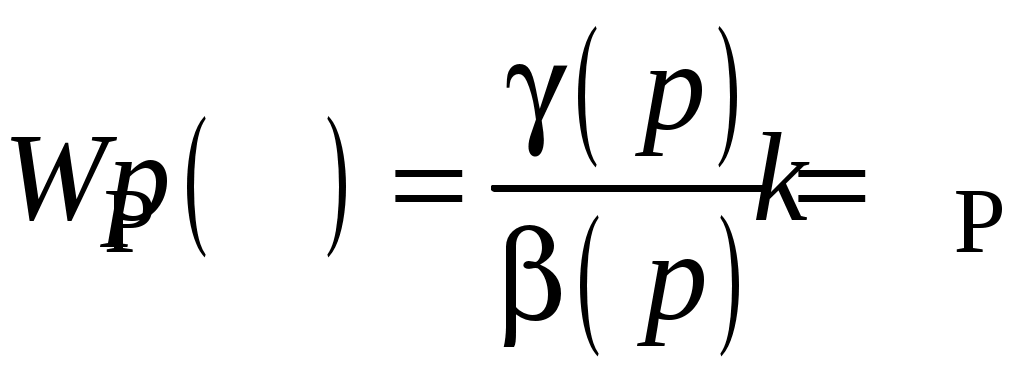11.4. Построение структурной схемы системы

При построении структурной схемы системы, приведенной в задании, воспользуемся передаточными функциями элементов, которые были получены выше. Полученная структурная схема системы изображена на рис. 60.


на ОУ







k_СП






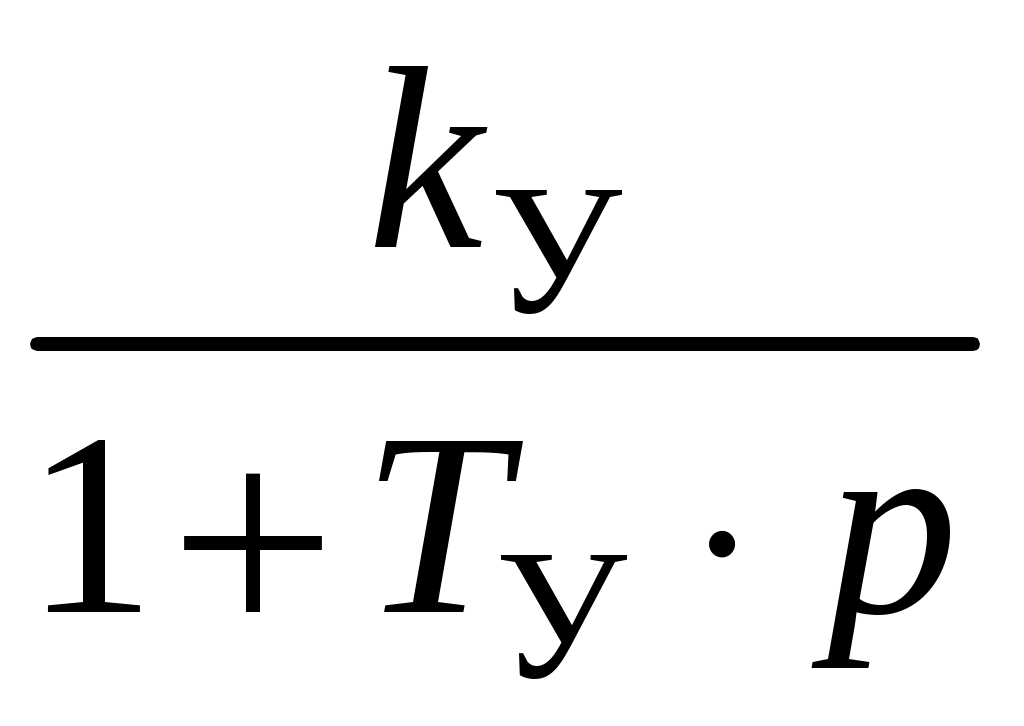
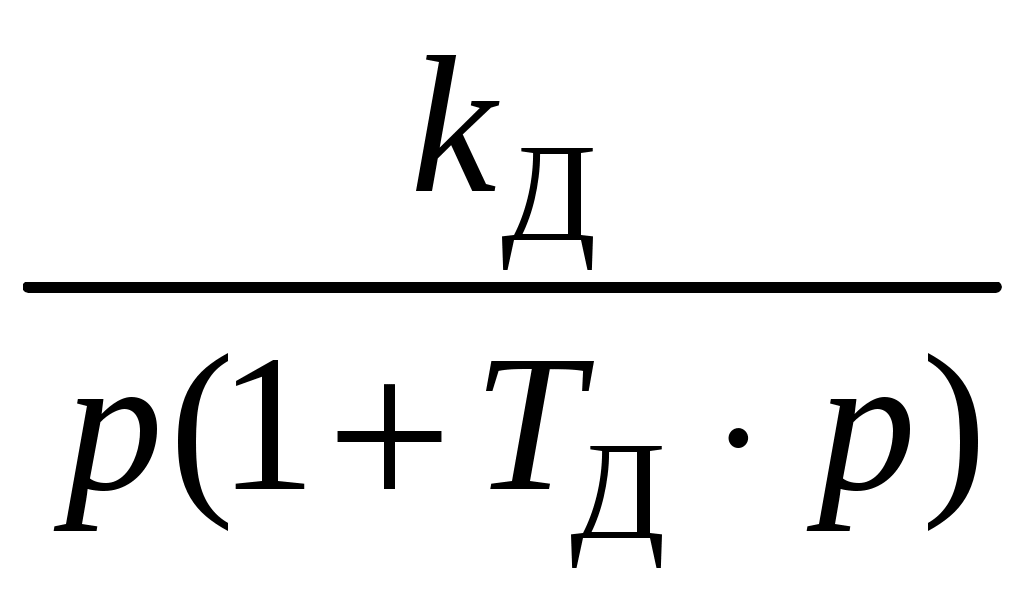
k_Р









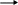
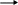
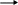
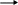
Рис.60. Структурная схема системы

11.5. Построение логарифмических частотных
характеристик разомкнутой системы

Для построения логарифмических частотных характеристик необходимо найти передаточную функцию всей системы. Так как данная система состоит из включенных последовательно звеньев, то передаточная функция разомкнутой системы будет равна произведению передаточных функций отдельных звеньев:



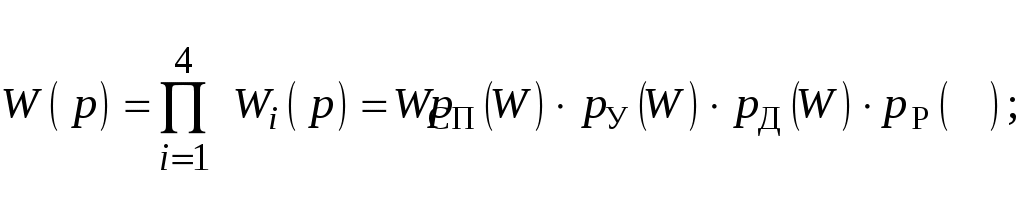
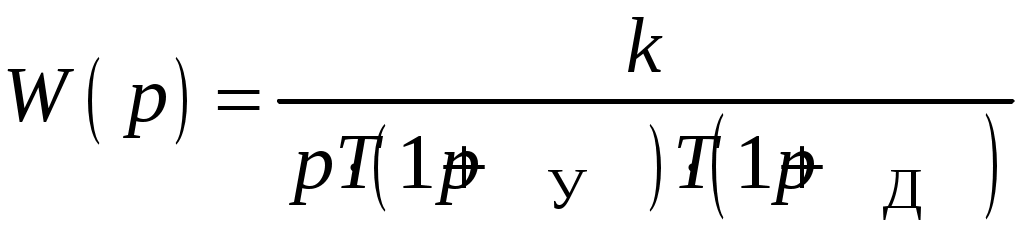, (4)

где k – общий коэффициент усиления разомкнутой цепи.

В выражении (4) параметры k, имеют следующие числовые
значения:



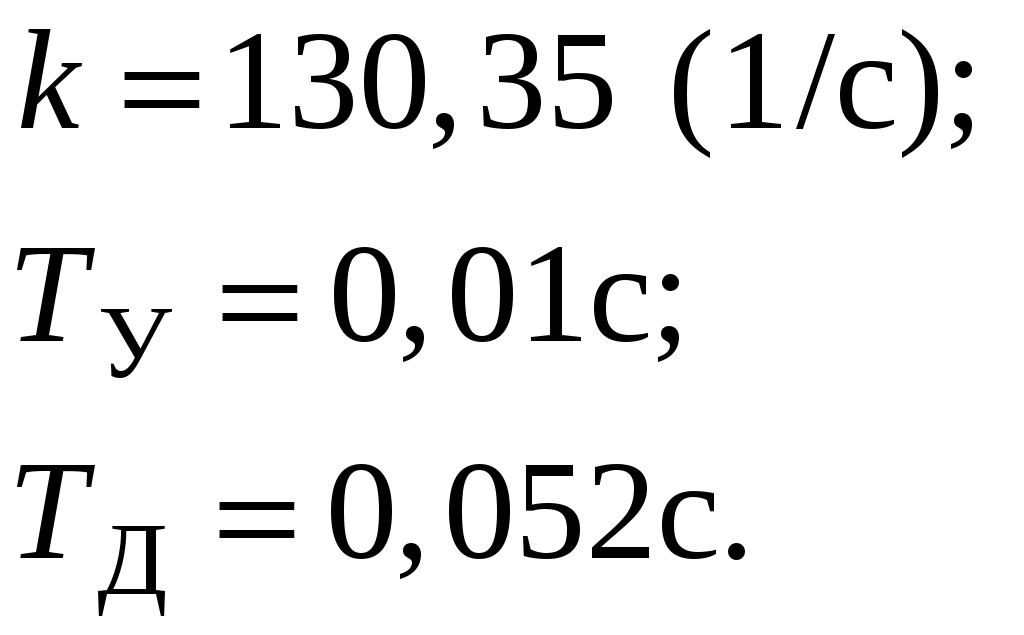
1. Логарифмическая амплитудно-частотная характеристика

---

ЛАЧХ следящей системы с передаточной функцией (4) имеет следующий вид:

;

;

.

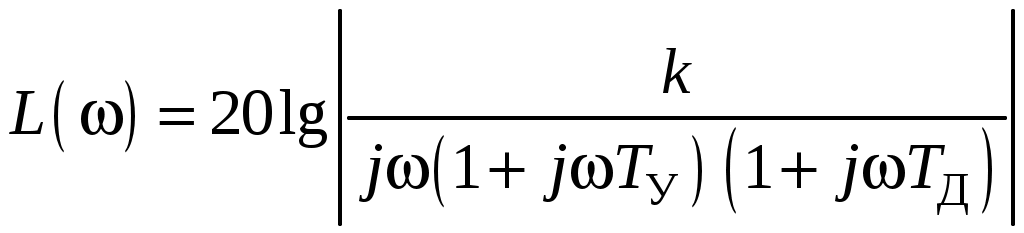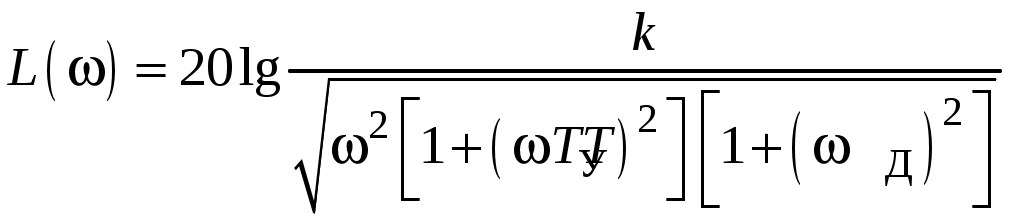Учитывая, что наибольшей постоянной времени соответствует наименьшее значение частоты, определяем сопрягающие частоты, начиная с меньшей:

, ;

, .

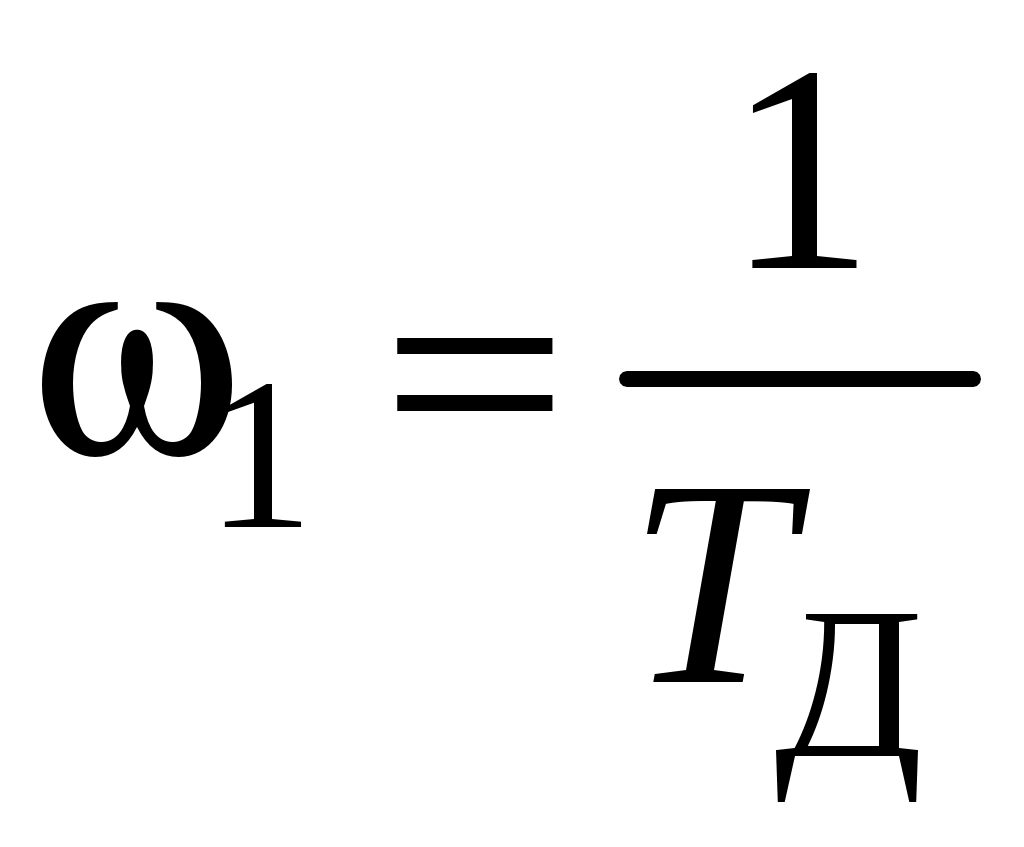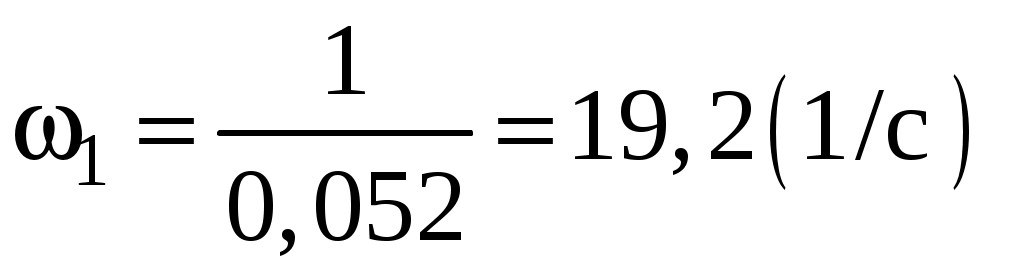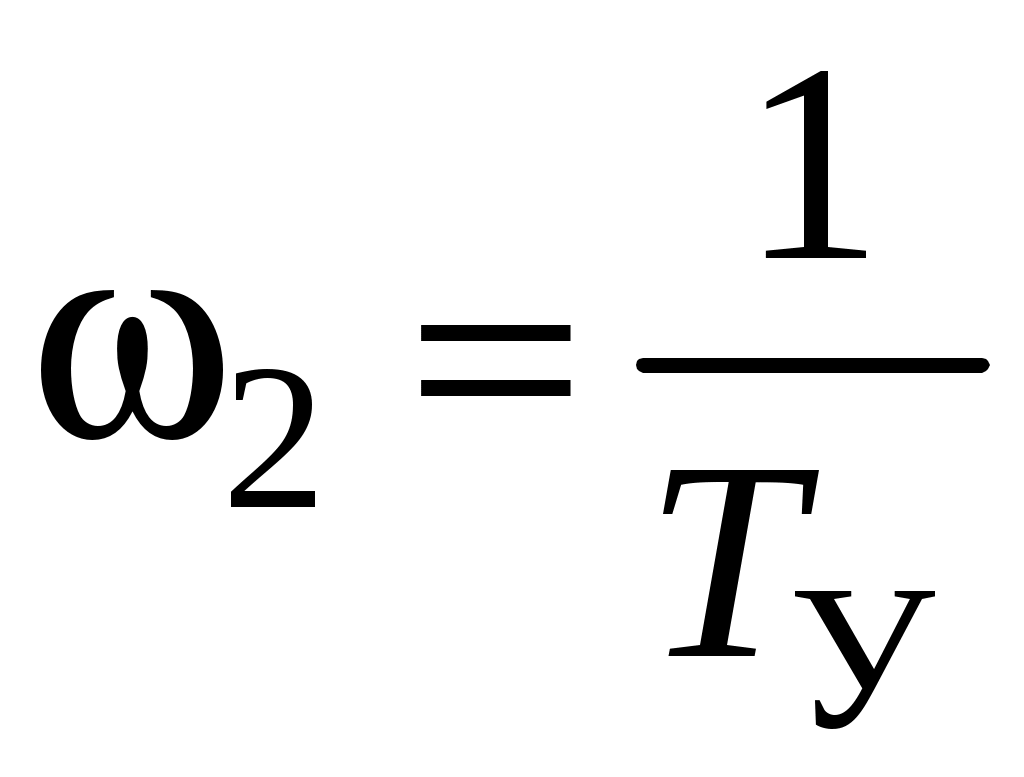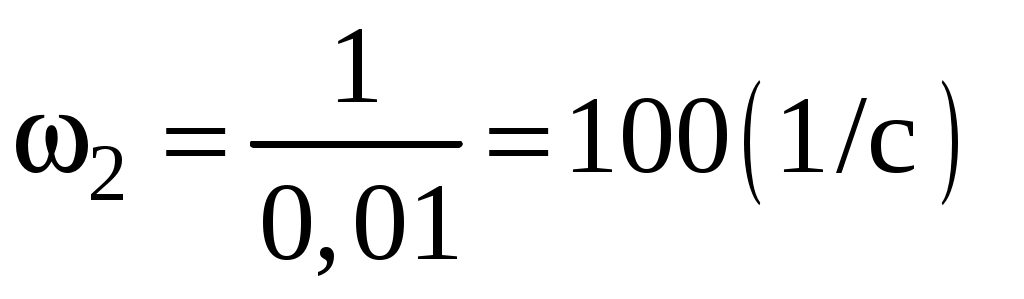Переходя к декадам, получаем:

;

.

Наносим сопрягающие частоты на график (рис. 61).

Находим точку и наносим её на верхний график.

Учитывая, что v =1 (где v – число, указывающее на порядок астатизма системы), т. к. в знаменателе равенства (4) стоит p, проводим низкочастотную асимптоту с наклоном до точки, соответствующей , с таким расчётом, чтобы эта асимптота пересекала ось ординат в точке 42,3 дБ.


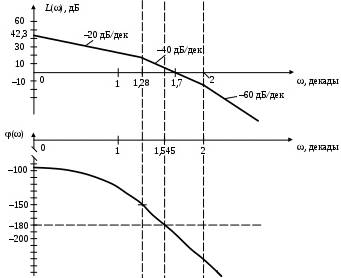
Рис. 61. ЛАЧХ и ЛФЧХ системы без обратной связи

Так как постоянная , определяющая частоту ₁, стоит в знаменателе передаточной функции (4), то увеличиваем наклон следующего участка характеристики на 20 дБ/дек (отклоняем характеристику вниз) и проводим его с наклоном –40 дБ/дек до точки, соответствующей ₁ = 2 декадам.

Постоянная времени

---

, определяющая частоту ₂, стоит в знаменателе выражения (4), поэтому наклон следующего участка увеличиваем на 20 дБ/дек и проводим её последний участок с наклоном –60 дБ/дек

Полученная ЛАЧХ изображена на рис. 61 (верхний график).

2. Логарифмическая фазочастотная характеристика.

Формула ЛФЧХ следящей системы с передаточной функцией (4) имеет следующий вид:

.

Это выражение позволяет построить двумя способами:

– по точкам;

– как сумму ординат ЛФЧХ двух апериодических звеньев с постоянными времени , и интегрирующего звена.

Построим ЛФЧХ по точкам.

Наносим сопрягающие частоты , рассчитанные для ЛАЧХ, на график (см. рис. 61). Далее строим ЛФЧХ по значениям, приведенным в табл. 2.
Таблица 2

Значения ЛФЧХ

с–1	дек	град	рад		с–1	дек	град	рад
1	0	–93,9	–1,48		60	1,78	–204,7	–3,21
2	0,3	–97,9	–1,54		70	1,85	–211,2	–3,33
3	0,48	–101,8	–1,6		80	1,9	–217,2	–3,42
4	0,6	–105,6	–1,66		90	1,95	–223,2	–3,51
5	0,7	–109,4	–1,72		100	2	–227,9	–3,58
6	0,78	–113,1	–1,78		110	2,04	–232	–3,64
7	0,85	–116,8	–1,83		120	2,08	–235,7	–3,7
8	0,9	–120,2	–1,89		130	2,11	–238,9	–3,75
9	0,95	–123,6	–1,94		140	2,15	–241,8	–3,79
10	1	–126,9	–1,99		150	2,18	–244,4	–3,84
20	1,3	–153,8	–2,42		160	2,2	–246,8	–3,88
30	1,48	–172,3	–2,71		170	2,23	–248,9	–3,91
40	1,6	–185,7	–2,92		180	2,26	–250,9	–3,94
50	1,7	–196,14	–3,08		190	2,28	–252,7	–3,96
					200	2,3	–254,3	–3,99

---

Полученная ЛФЧХ изображена на рис. 61 (нижний график).

---