Файл: Учебное пособие Рыбинск 2007 удк 681. 5 Павлов Р. В. Основы теории управления. Учебное пособиергата. Рыбинск, 2007. 83 с.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 271
Скачиваний: 2
СОДЕРЖАНИЕ
1. Основные понятия и определения
3. Дифференциальные уравнения ипередаточные функции
5. Типовые звенья САУ и их характеристики
6. Построение передаточных функций САУ
7. Составление исходных дифференциальныхуравнений САУ
9. Процесс управления и требования к нему
9.1. Оценка устойчивости линейной САУ
9.3. Качество переходного процесса
10.2. Типы корректирующих устройств
10.3. Пример синтеза последовательного корректирующего устройства
10.4. Пример синтеза параллельного корректирующего устройства
11.3. Определение передаточных функций элементов системы
11.4. Построение структурной схемы системы
11.5. Построение логарифмических частотных характеристик разомкнутой системы
11.6. Определение устойчивости и запасаустойчивости по амплитуде и фазе
11.7. Определение критического значения добротностис помощью критерия Гурвица
11.8. Введение скоростной обратной связи
11.9. Нахождение минимального коэффициентаскоростной обратной связи
11.10 Определение оптимального коэффициентаскоростной обратной связи
12.2. Характеристики случайных величин и процессов
12.3. Прохождение случайного сигнала через линейную непрерывную систему
12.4. Расчет установившейся ошибки САУ
12.5. Расчеты по минимуму ошибки
13.1. Общий метод составления уравнений нелинейных САУ
13.3. Устойчивость по Ляпунову
Повышается порядок астатизма системы. Однако переходный процесс затягивается и ухудшается устойчивость САУ. Вносится отрицательный сдвиг фаз и происходит подавление высоких частот.
3. Дифференцирующее корректирующее звено.
Звено описывается соотношениями:
Звено подавляет низкие частоты и вносит положительный сдвиг фаз. Однако подавление низких частот обычно недопустимо, т. к. снижает общий результирующий коэффициент усиления САУ.
4. Интегро-дифференцирующее звено.
Один из вариантов имеет характеристику
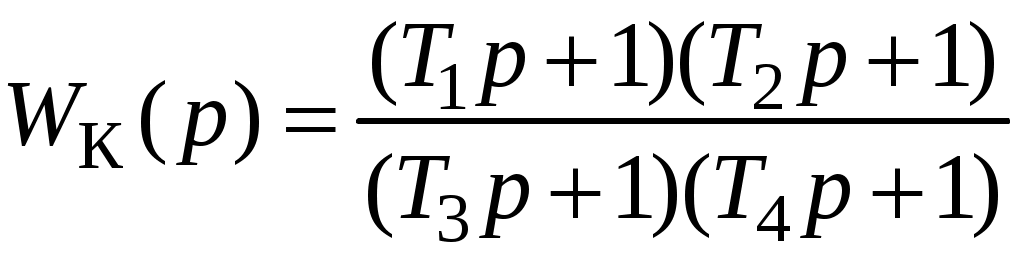 ;
;Такое звено представляет собой полосовой фильтр: происходит подавление частот в некотором диапазоне. Вносимый фазовый сдвиг меняет значение от отрицательного до положительного.
10.2.2. Параллельные корректирующие устройства.
Их удобно применять при использовании сложных законов управления, когда наряду с основным сигналом вводятся его производные или интегралы.
1. Введение производной от ошибки (рис. 49).
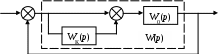
Рис. 49. Параллельное корректирующее устройство
Применяется дифференцирующее звено с характеристикой
Получаем результирующие характеристики разомкнутой САУ:
Происходит поднятие верхних частот, улучшается скорость реакции САУ, вносится положительный сдвиг фаз.
2. Местная обратная связь
Как известно, обратная связь бывает отрицательной и положительной, а также жесткой и гибкой.
Жесткая – это постоянно действующая; гибкая – действует только во время переходного процесса.
Рассмотрим варианты использования такого способа коррекции.
2.1. Положительная жесткая обратная связь.
В качестве исходного звена рассмотрим инерционное звено первого порядка, в качестве корректирующего – пропорциональное (рис. 50).
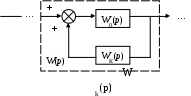
Рис. 50. Положительная жесткая обратная связь
Параметры звеньев следующие:
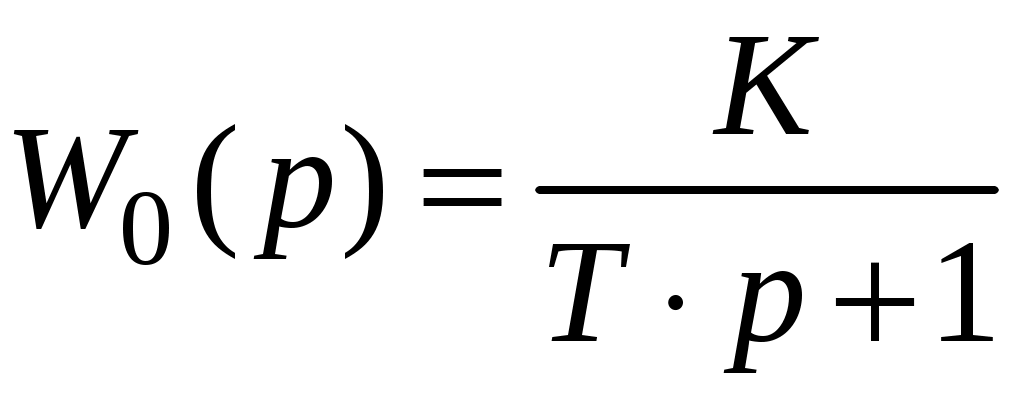 ;
;Передаточная функция результирующего звена
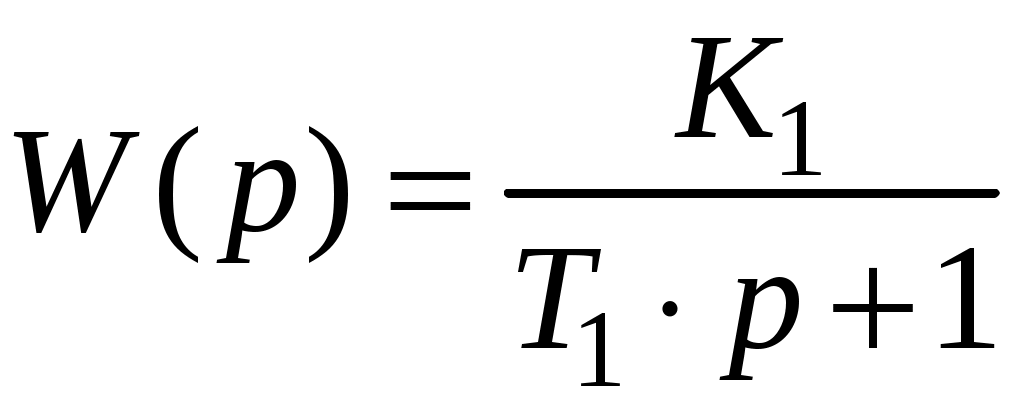 ;
;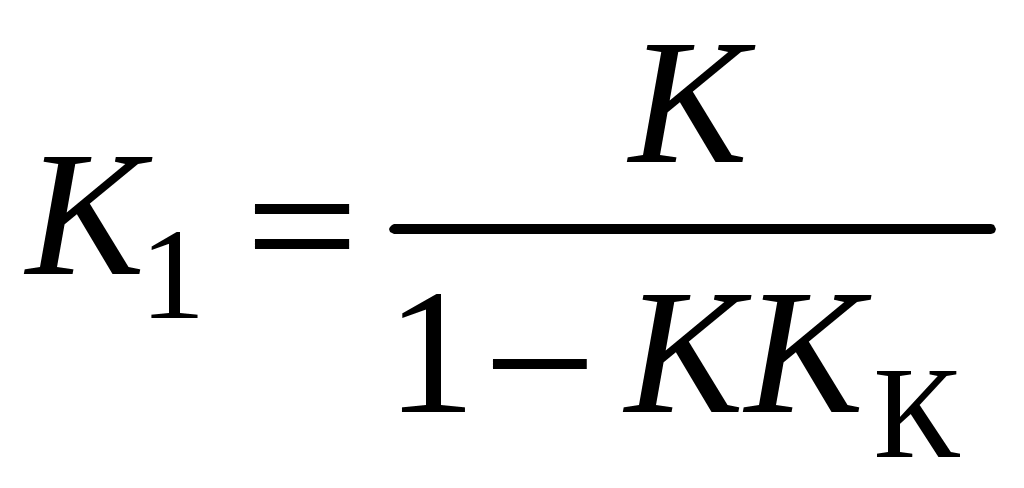 ;
;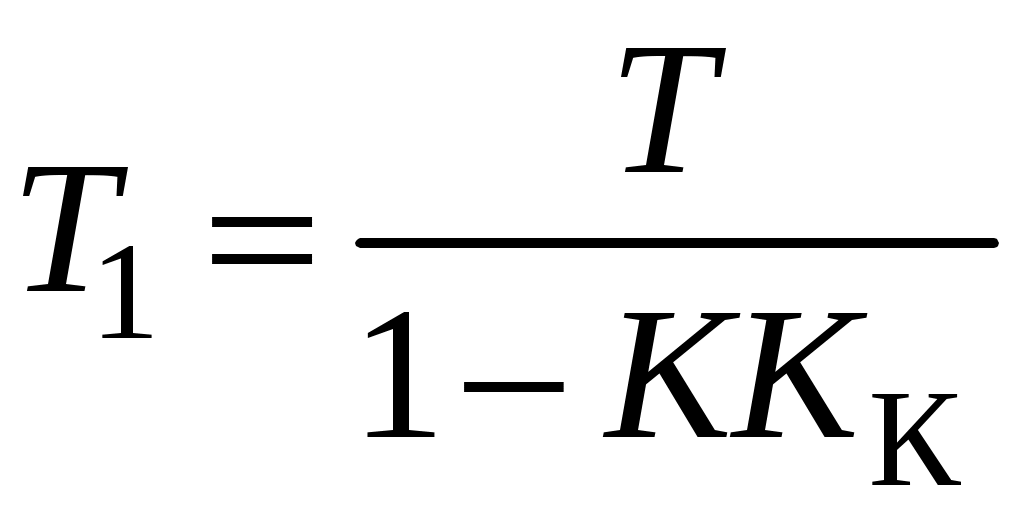 .
.Тип звена не изменился. Коэффициент усиления увеличился, но возросла и постоянная времени звена, т. е. переходный процесс стал медленней, что является недостатком.
2.2. Отрицательная жесткая обратная связь.
а. Рассмотрим звенья с теми же параметрами (рис. 51).
Передаточная функция результирующего звена
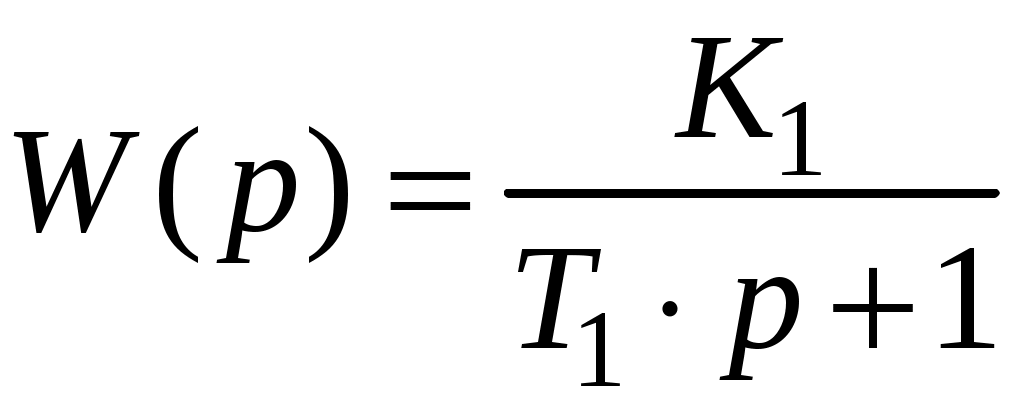 ;
;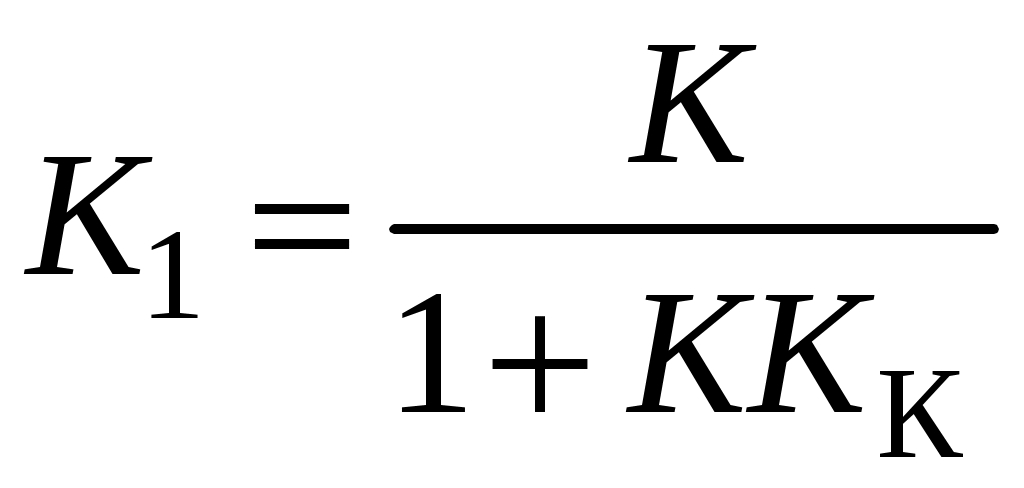 ;
;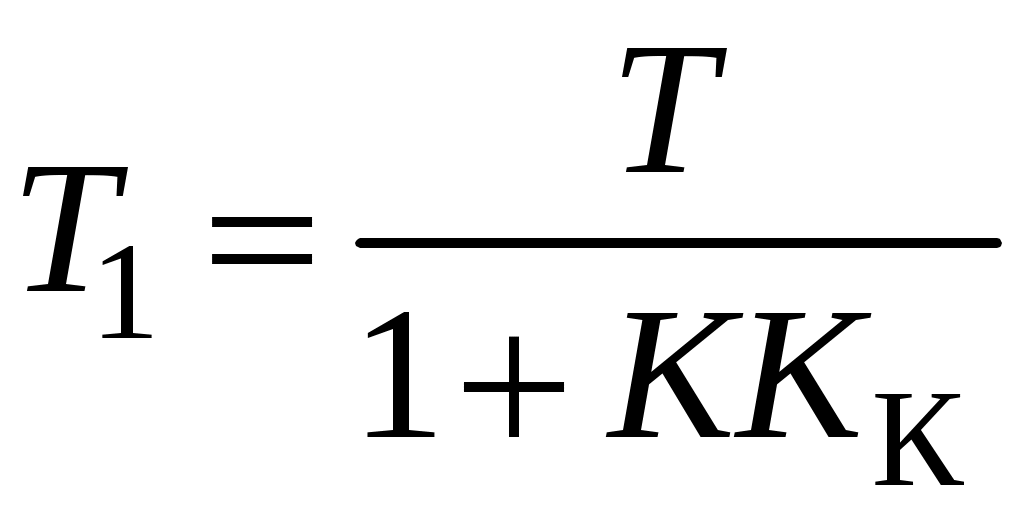 .
.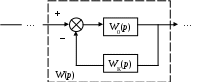
Рис. 51 . Отрицательная жесткая обратная связь
Параметры звена улучшились за счет уменьшения его инерционности (уменьшение постоянной времени). Некоторое снижение общего коэффициента усиления (K1) можно компенсировать другими звеньями.
б. Исходное звено – интегрирующее, корректирующее – пропорциональное.
Как известно, интегрирующее звено является неустойчивым.
Его передаточная функция
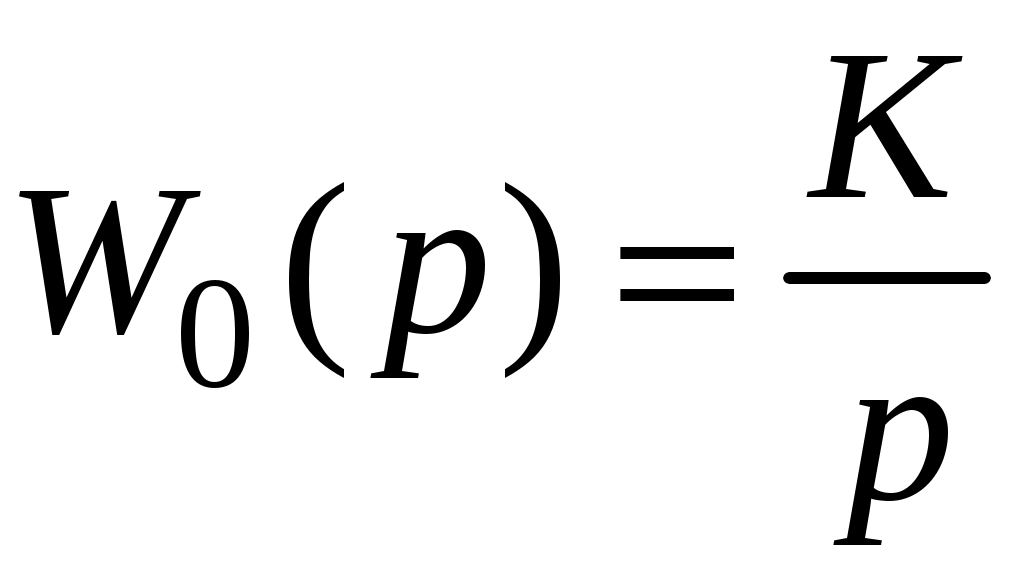
.
Передаточная функция результирующего звена
 ;
;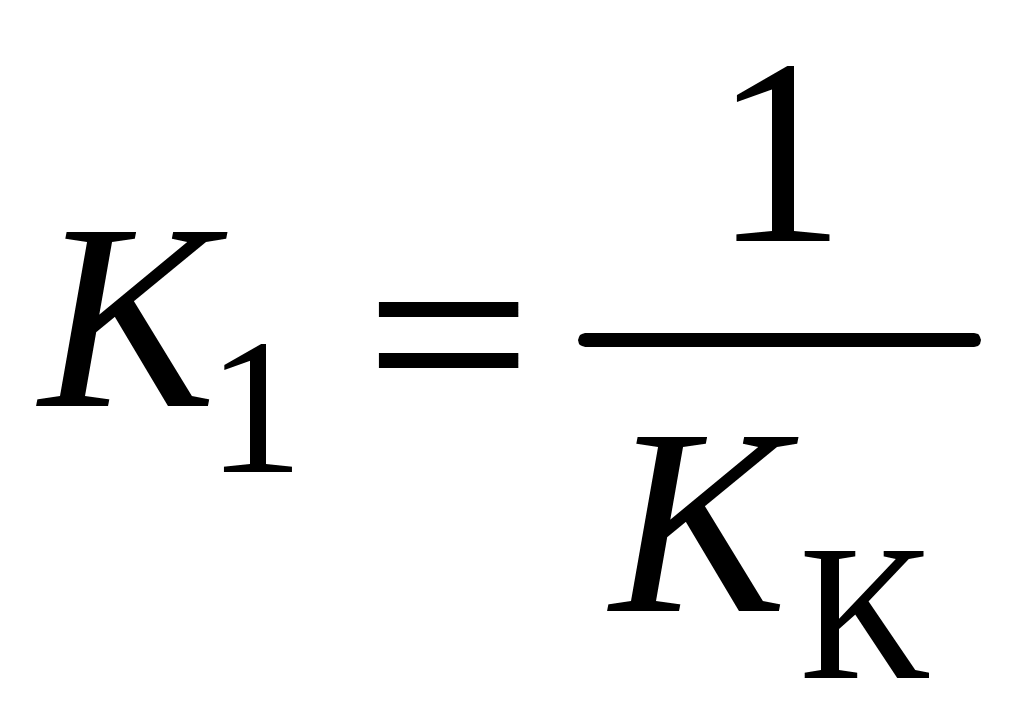 ;
;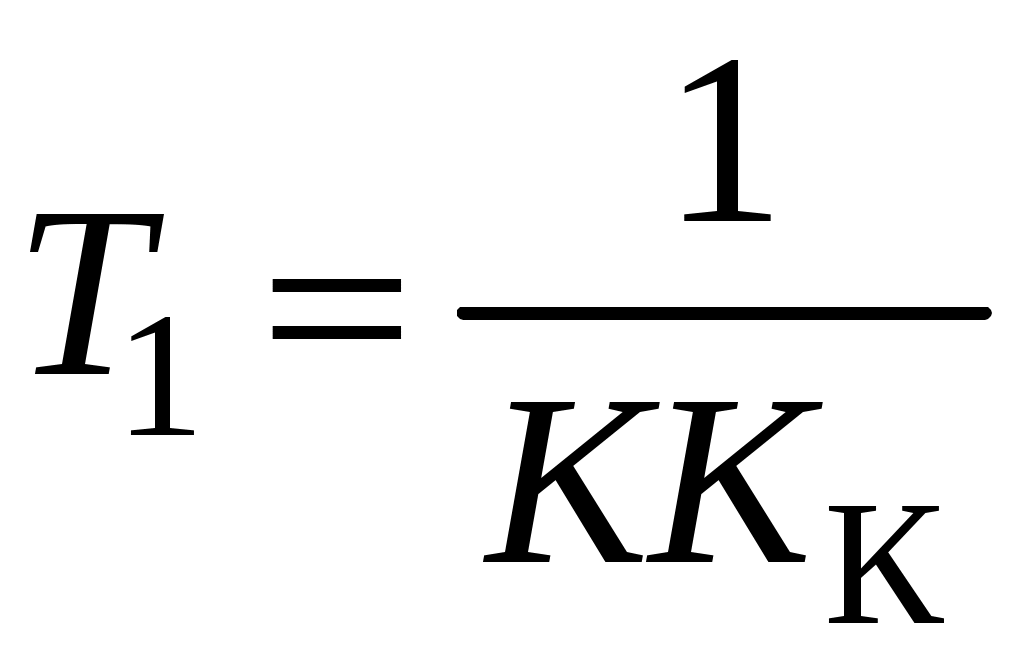 .
.Результирующее звено стало апериодическим и приобрело устойчивость.
3. Гибкая отрицательная обратная связь.
Рассмотрим колебательное звено с передаточной функцией
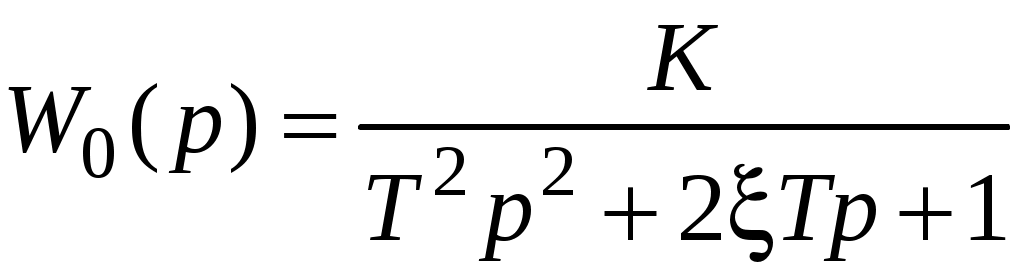 .
.Корректирующим звеном является дифференцирующее звено с передаточной функцией
Результирующая передаточная функция имеет вид:
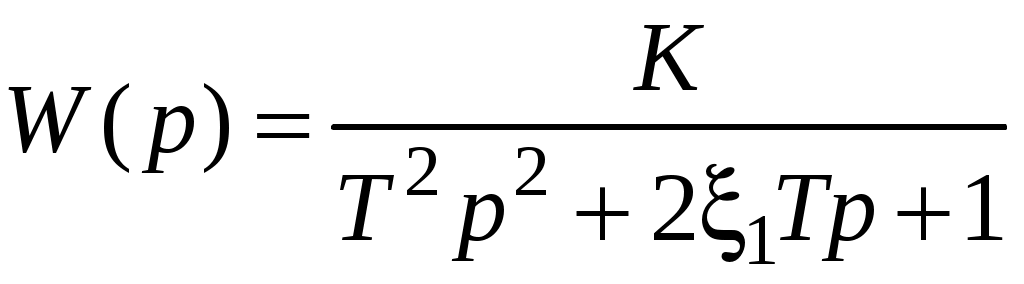 ;
;Характер звена не изменился, однако коэффициент затухания увеличился, а коэффициент передачи остался прежним. Переходный процесс стал менее колебательным (увеличились демпфирующие свойства системы). Более того, можно таким образом подобрать параметры корректирующего звена, что результирующее звено станет апериодическим звеном второго порядка (если коэффициент затухания станет больше единицы).
10.2.3. Коррекция по внешнему воздействию
Как известно, основной принцип автоматического управления – это формирование управляющего сигнала по величине ошибки.
Если вводится корректирующего устройство по внешнему воздействию, то имеет место комбинированное управление: по ошибке и по внешнему воздействию. Управление по ошибке представляет собой замкнутый контур управления, а коррекция по внешнему воздействию – разомкнутый контур.
В этом случае, при определенных условиях, установившуюся ошибку САУ можно свести к нулю при любой форме внешнего воздействия. Это свойство называется инвариантностью (независимость, нечувствительность) системы к внешнему воздействию.
Как известно, входными воздействиями являются задающее и возмущающее. Рассмотрим оба варианта коррекции.
1. Коррекция по задающему воздействию.
Структурная схема САУ имеет вид (рис. 52).
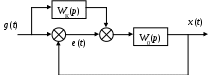
Рис. 52. Коррекция по задающему воздействию
Найдем эквивалентную передаточную функцию замкнутой системы по задающему воздействию
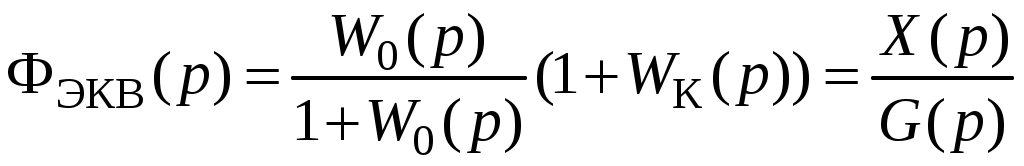 .
.Аналогично, можно найти передаточную функцию замкнутой системы по ошибке
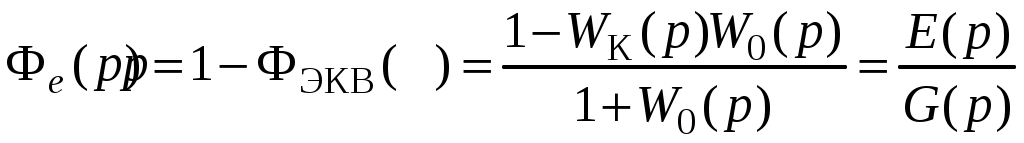 ,
,где
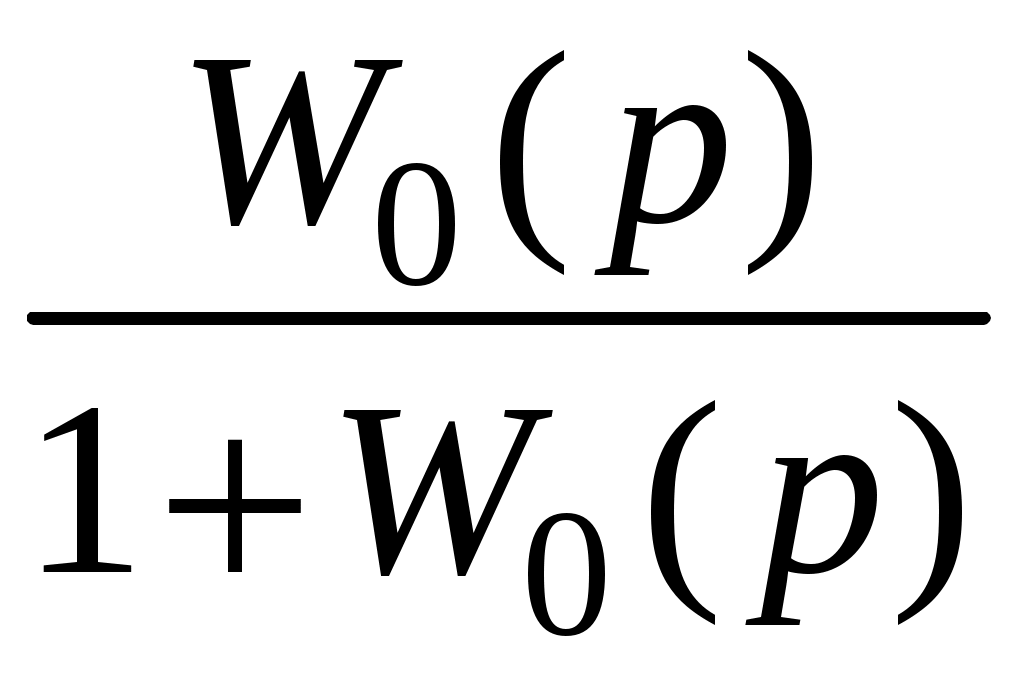 – это передаточная функция исходной замкнутой системы.
– это передаточная функция исходной замкнутой системы.Можно заметить, что знаменатели функций после введения корректирующего звена не изменились.
Так как 1 + W0(p) – это характеристический полином системы, определяющий вид переходного процесса САУ, то можно сделать вывод, что вид переходного процесса после введения корректирующего звена не меняется, следовательно, не меняется устойчивость системы.
Найдем условие равенства нулю установившейся ошибки.
Это условие обеспечивается, если передаточная функция замкнутой системы по ошибке будет равна 0. Отсюда следует, что
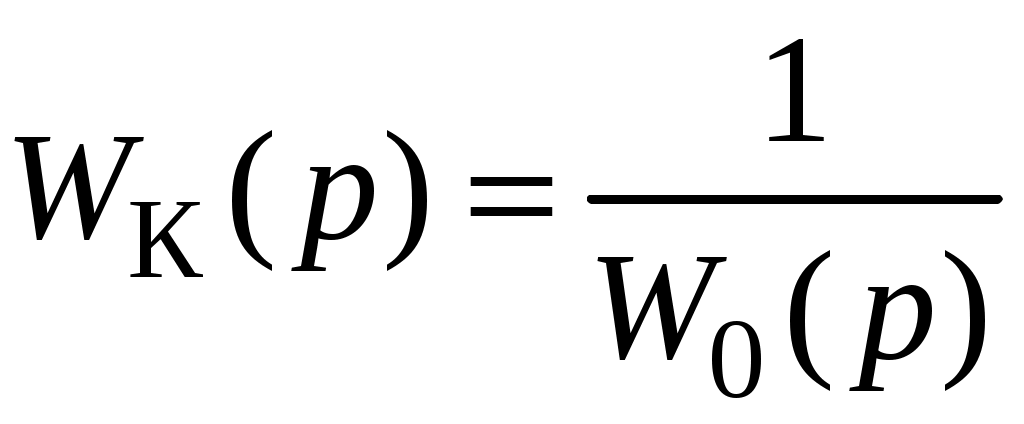 .
.Это выражение можно представить в виде ряда
Ряд бесконечный, следовательно, полной инвариантности САУ достичь невозможно (нужно брать бесконечное число производных от входного сигнала). Поэтому ограничиваются частичной инвариантностью, т. е. в передаточной функции корректирующего звена оставляют несколько первых членов ряда.
2. Коррекция по возмущению.
Структурная схема САУ без коррекции имеет вид (рис. 53).
Введем корректирующее звено (рис. 54).
Передаточная функция замкнутой системы по возмущающему воздействию будет иметь вид:
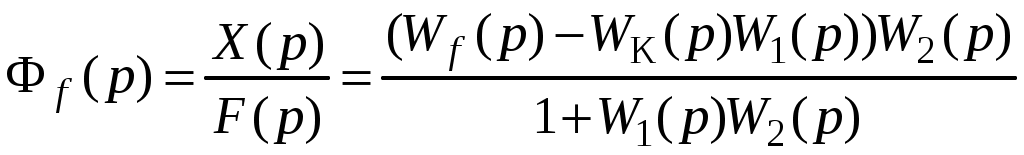 .
.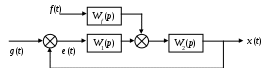
Рис. 53. Структура САУ с возмущающим воздействием
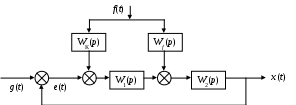
Рис. 54. Коррекция по возмущению
Чтобы устранить влияние на выходной сигнал возмущающего воздействия, нужно обеспечить Фf(p) = 0. При этом получим
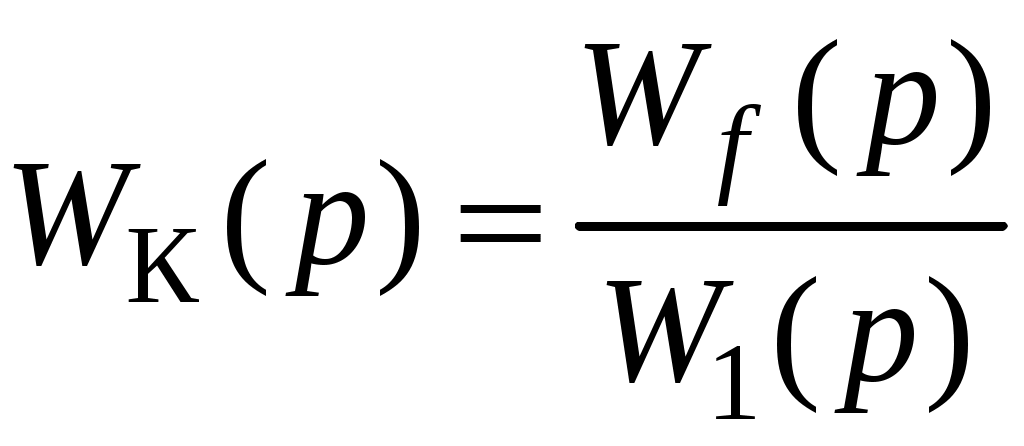
.
Это выражение можно представить в виде ряда
Ряд бесконечный, следовательно, полной инвариантности САУ достичь невозможно (нужно брать бесконечное число производных от сигнала). Поэтому ограничиваются частичной инвариантностью, т. е. в передаточной функции корректирующего звена оставляют несколько первых членов ряда.
10.2.4. Неединичная главная обратная связь
Структурная схема САУ имеет вид (рис. 55).
Входной сигнал g(t) сравнивается не с выходным x(t), а с промежуточным z(t).
Передаточная функция замкнутой системы
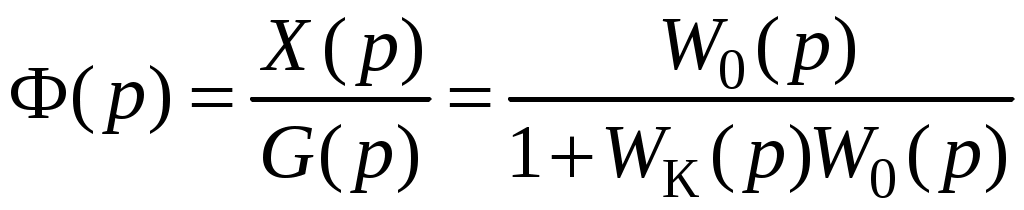 .
.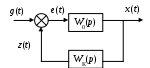
Рис. 55. Неединичная главная обратная связь
Полная инвариантность достигается, когда входной и выходной сигналы совпадают, т. е. числитель и знаменатель этого выражения равны. Отсюда следует:
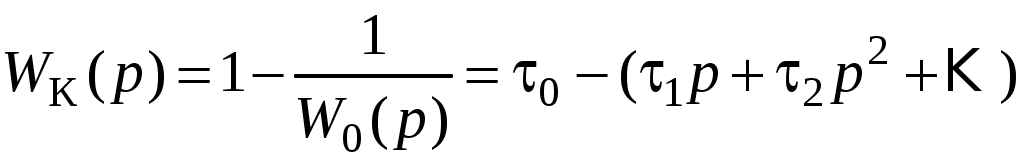 .
.Имеет место положительная обратная связь по производной.
Недостаток данного подхода состоит в том, что в этом случае меняется характеристическое уравнение системы, следовательно, ухудшается устойчивость САУ и меняется вид переходного процесса.