Файл: Учебное пособие Рыбинск 2007 удк 681. 5 Павлов Р. В. Основы теории управления. Учебное пособиергата. Рыбинск, 2007. 83 с.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 287
Скачиваний: 2
СОДЕРЖАНИЕ
1. Основные понятия и определения
3. Дифференциальные уравнения ипередаточные функции
5. Типовые звенья САУ и их характеристики
6. Построение передаточных функций САУ
7. Составление исходных дифференциальныхуравнений САУ
9. Процесс управления и требования к нему
9.1. Оценка устойчивости линейной САУ
9.3. Качество переходного процесса
10.2. Типы корректирующих устройств
10.3. Пример синтеза последовательного корректирующего устройства
10.4. Пример синтеза параллельного корректирующего устройства
11.3. Определение передаточных функций элементов системы
11.4. Построение структурной схемы системы
11.5. Построение логарифмических частотных характеристик разомкнутой системы
11.6. Определение устойчивости и запасаустойчивости по амплитуде и фазе
11.7. Определение критического значения добротностис помощью критерия Гурвица
11.8. Введение скоростной обратной связи
11.9. Нахождение минимального коэффициентаскоростной обратной связи
11.10 Определение оптимального коэффициентаскоростной обратной связи
12.2. Характеристики случайных величин и процессов
12.3. Прохождение случайного сигнала через линейную непрерывную систему
12.4. Расчет установившейся ошибки САУ
12.5. Расчеты по минимуму ошибки
13.1. Общий метод составления уравнений нелинейных САУ
13.3. Устойчивость по Ляпунову
1. Реакцией САУ или звена на единичное входное воздействие называется переходная характеристика или переходная функция h(t) (рис. 5).

Рис. 5. Пример переходной характеристики
При использовании преобразования Лапласа получим
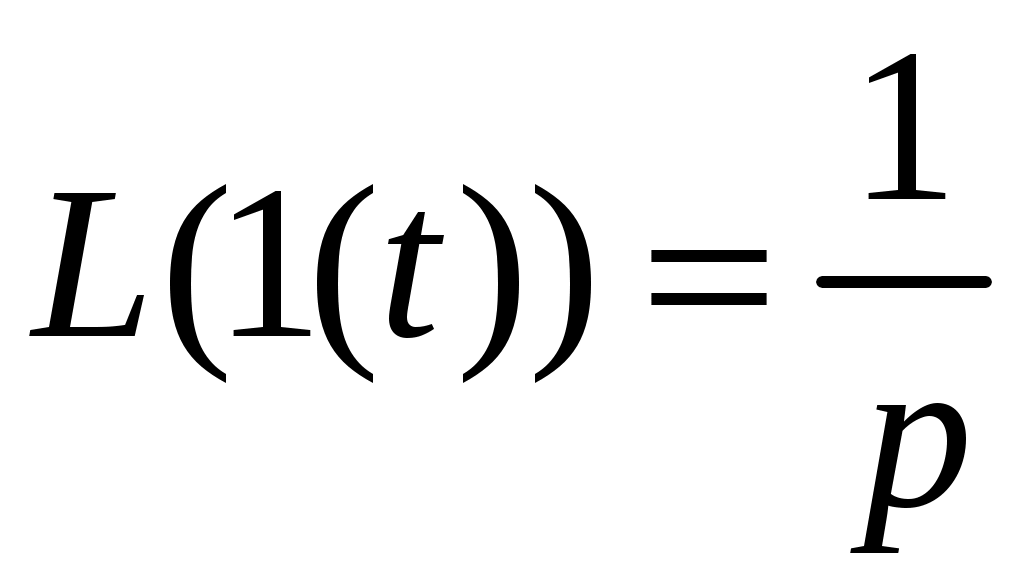 ,
,тогда изображение переходной характеристики
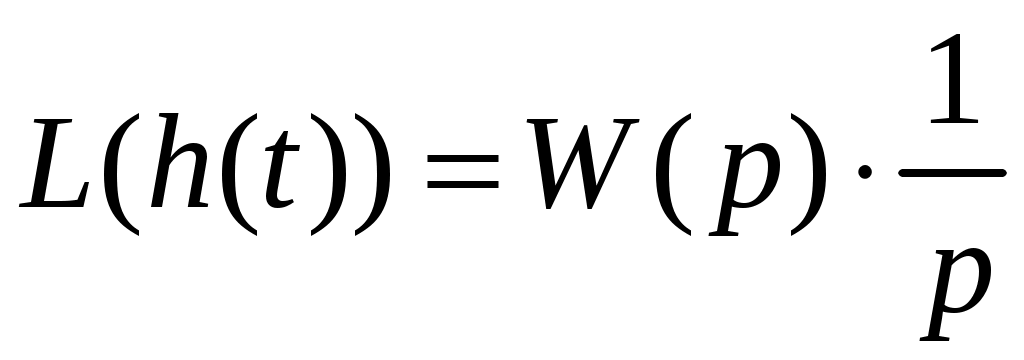 .
.2. Реакцией системы на сигнал вида (t) является весовая функция (t) (рис. 6).
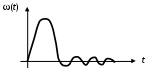
Рис. 6. Пример весовой функции САУ
При использовании преобразования Лапласа получим следующие соотношения:
Преобразованием Лапласа от весовой функции является передаточная функция.
Весовая функция и переходная характеристика связаны простым соотношением
Описание САУ во временной области через весовую функцию эквивалентно описанию передаточной функцией в области изображений.
Можно найти реакцию системы на произвольный входной сигнал. Для этого можно воспользоваться интегралом Дюамеля или интегралом свертки
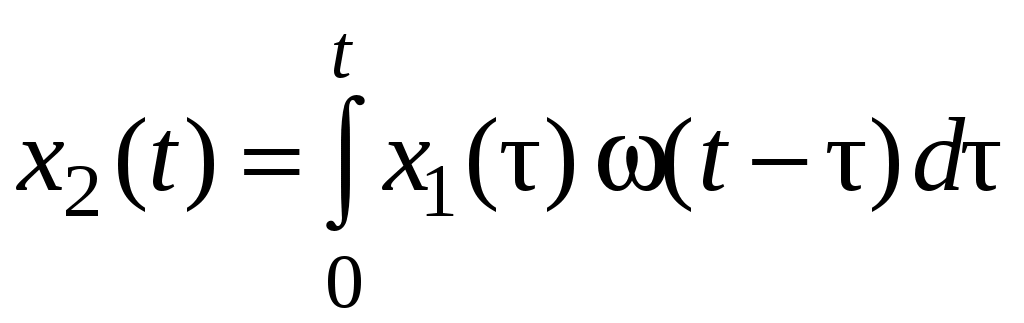 .
.3. Если используется входной сигнал вида Аsint, то говорят о частотных характеристиках системы.
Частотные характеристики – это выражения и графические зависимости, выражающие реакцию исследуемой САУ на сигнал вида Аsint при различных значениях частоты .
На выходе САУ сигнал будет иметь вид
где A(t) – амплитуда сигнала, (t) – сдвиг фазы.
Частотную передаточную функцию для получения частотных характеристик можно представить в следующем виде:
;
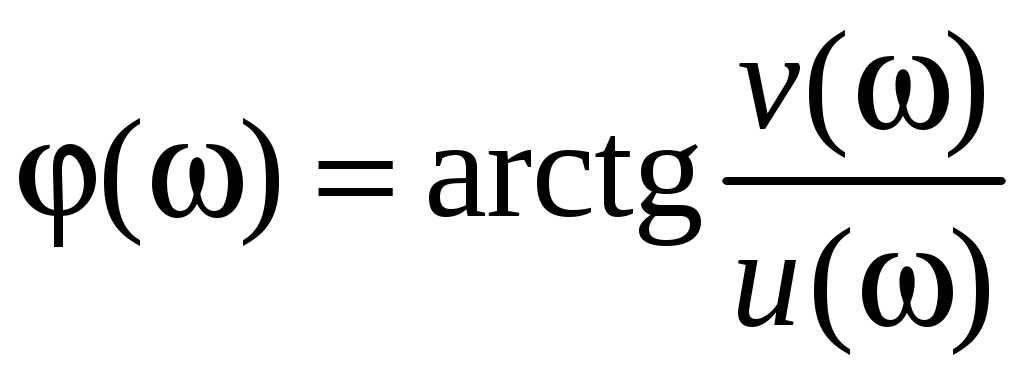 , (1)
, (1)где u() и v() – действительная и мнимая части комплексного выражения.
Вещественная часть состоит из четных степеней частоты , а мнимая – из нечетных.
Эту функцию можно представить графически на комплексной плоскости. Такое изображение называется годографом (рис. 7) или амплитудно-фазовой характеристикой. Кривая строится путем получения точек на плоскости при задании определенных значений частоты и расчете u() и ().
Для получения графика в случае отрицательных частот необходимо сделать зеркальное отображение имеющейся характеристики относительно действительной оси.
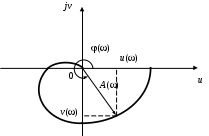
Рис. 7. Годограф или амплитудно-фазовая характеристика системы
Аналогичным образом можно построить отдельно графики длины вектора А() и угла поворота (). Тогда получим амплитудно-частотную и фазо-частотную характеристики.
На практике часто используют логарифмические характеристики. Логично использовать натуральный логарифм
Однако на практике используют десятичные логарифмы и получают логарифмическую амплитудно-частотную (ЛАЧХ) (рис. 8) и логарифмическую фазо-частотную (ЛФЧХ) характеристики (рис. 9).
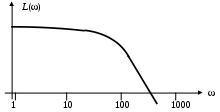
Рис. 8. Пример ЛАЧХ системы
ЛАЧХ определяется по формуле
где |W(j)| – модуль частотной передаточной функции.
Единицей измерения является децибел.
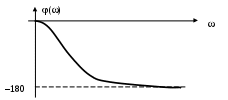
Рис. 9. Пример ЛФЧХ системы
При вычислении логарифмической фазочастотной характеристики используется (1).
При построении графиков по оси абсцисс откладывают частоту в логарифмическом масштабе. Так как при вычислении значений ЛАЧХ в выражениях используются зависимости от степени , то график имеет стандартный наклон, кратный 20 дБ/дек. Дек – декада, т. е. изменение частоты на порядок.
Теоретически точка = 0 на оси частот должна быть слева в бесконечности, но для практических расчетов ось ординат сдвигают вправо.
Логарифмические характеристики имеют следующие достоинства:
– простота построения;
– легкость получения ЛАЧХ системы из ЛАЧХ звеньев путем геометрического сложения;
– простота анализа САУ.
5. Типовые звенья САУ и их характеристики
1. Усилительное (пропорциональное, безынерционное) звено (рис. 10).
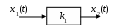
Рис. 10. Схема САУ с усилительным звеном
Дифференциальное уравнение звена имеет вид
Годограф звена, ЛАЧХ и ЛФЧХ представлен на рис. 11.

а) б) в)
Рис. 11. Частотные характеристики усилительного звена
а) годограф; б) ЛАЧХ; в) ЛФЧХ
2. Инерционное или апериодическое звено I порядка.
Общий вид схемы САУ представлен на рис 12.

Рис. 12. Структурная схема звена
Дифференциальное уравнение
Передаточная функция получается следующим образом:
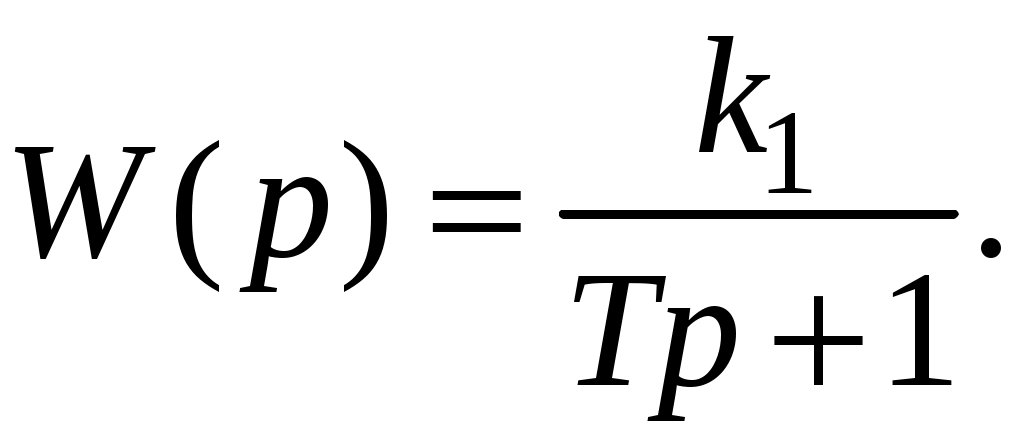
Весовая функция и переходная характеристика выражаются соотношениями h(t) = k1(1 – e–t/T) 1(t) и
Графики переходных процессов представлены на рис. 13.
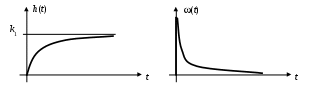
а) б)
Рис. 13. Переходные процессы инерционного звена 1-го порядка
а) переходная характеристика; б) весовая функция
Частотные характеристики получены из соотношений:
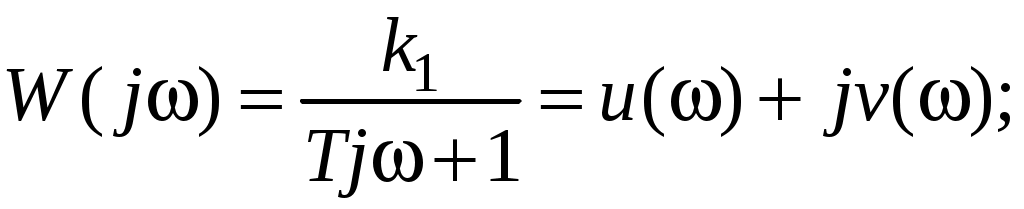
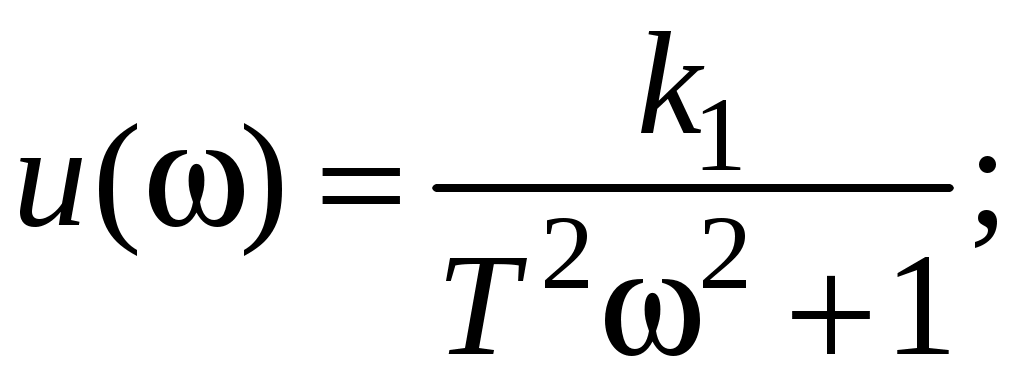
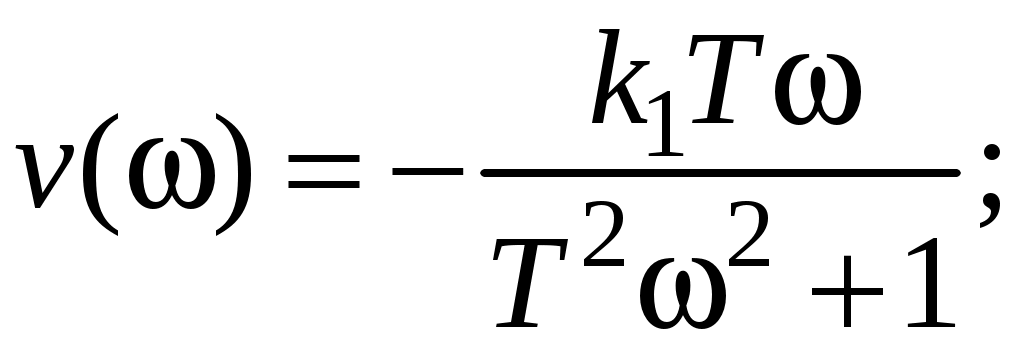
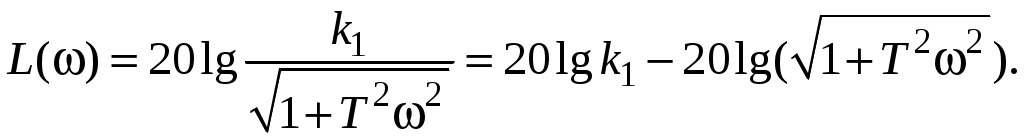
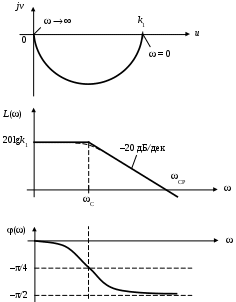
Их графики имеют вид (рис. 14).
а)
б)
в)
Рис. 14. Частотные характеристики инерционного звена 1-го порядка
а) годограф; б) ЛАЧХ; в) ЛФЧХ
С – сопрягающая частота;
СР – частота среза.
ЛАЧХ строится приближенно. Вся ось частот разбивается на 2 интервала
3. Апериодическое звено II порядка.
На основе ДУ можно получить выражение для передаточной функции
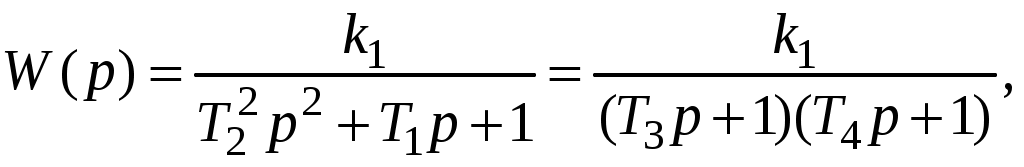
причем
Имеет место последовательное соединение двух апериодических звеньев первого порядка.
Логарифмические характеристики равны
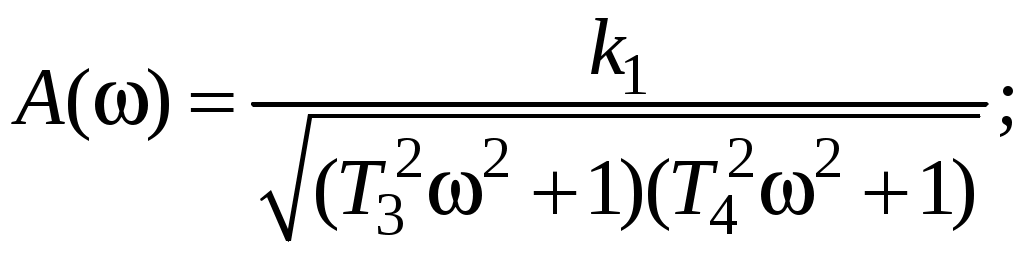
их графики представлены на рис. 15.
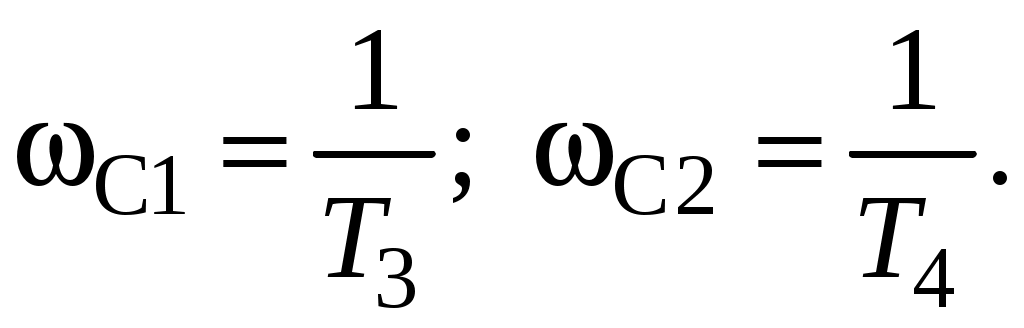
4. Колебательное и консервативное звенья.
Дифференциальное уравнение звеньев имеет вид звена 3, однако
Распространена следующая форма записи передаточной функции:
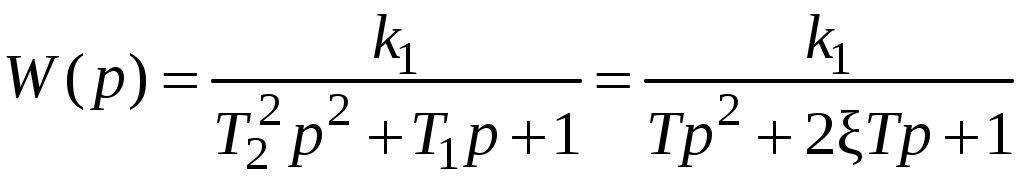 ,
,где
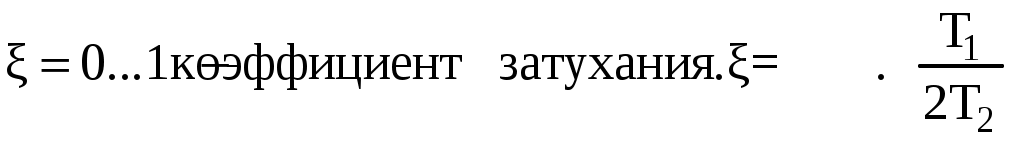
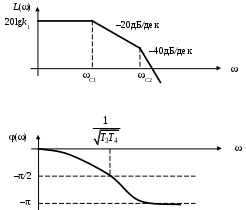
а)
б)
Рис. 15. Частотные характеристики апериодического звена II порядка
а) ЛАЧХ; б)ЛФЧХ
Переходная характеристика звена имеет вид (рис. 16).