Файл: Учебное пособие Рыбинск 2007 удк 681. 5 Павлов Р. В. Основы теории управления. Учебное пособиергата. Рыбинск, 2007. 83 с.doc

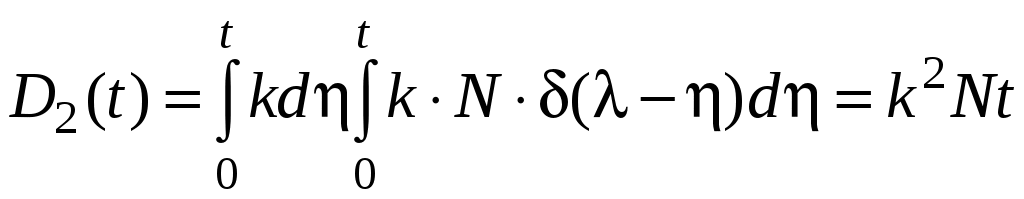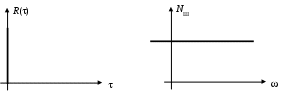
а) б)

Рис. 70. Характеристики БГШ
а) корреляционная функция; б) спектральная плотность

Анализ последнего выражения показывает, что дисперсия на выходе растет пропорционально времени и стремится к бесконечности. Это легко объяснить, если вспомнить, что данное звено является неустойчивым.

2. Расчеты в частотной области.

Более удобно для расчета параметров случайного сигнала на выходе пользоваться спектральными характеристиками.

Спектральную плотность на входе и выходе САУ можно определить через изображение Фурье входного S₁() и выходного S₂() сигналов

;

.

С другой стороны, для линейной САУ известно соотношение через частотную передаточную функцию:

.

Отсюда:

;

.

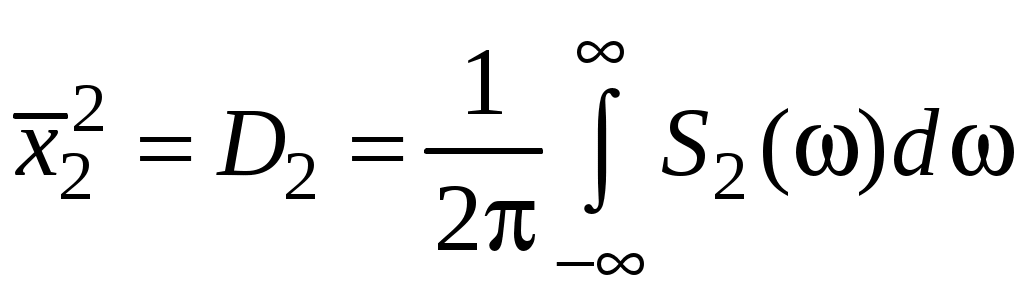Строго говоря, такой подход справедлив, если закон распределения случайной величины при прохождении через систему не меняется. Это выполняется в случае нормального закона распределения случайной величины. Плотность распределения вероятности этого закона

,

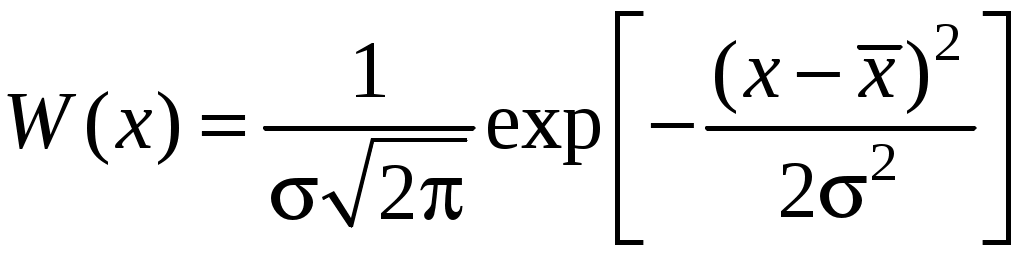где  – среднеквадратичное отклонение, а график представлен на рис. 71.

Рис. 71. Нормальный закон распределения случайной величины

12.4. Расчет установившейся ошибки САУ

Замкнутая система может находиться под воздействием случайного задающего сигнала g(t), и случайной помехи f(t), приложенной в произвольной точке системы (рис. 72).

Корреляционные функции и спектральные плотности и полезного сигнала и помехи известны. Конечная цель – нахождение корреляционной функции и спектральной плотности ошибки x(t) и выходного сигнала y(t).

Рис. 72. Случайный задающий сигнал и случайная помеха в САУ

Обычно ограничиваются более узкой задачей: нахождением среднеквадратичной ошибки (СКО) системы управления.

Возможны следующие случаи.

1. Имеется входной сигнал g(t) – случайный стационарный процесс. Помеха f(t) = 0.

Тогда спектральная плотность ошибки

,

где

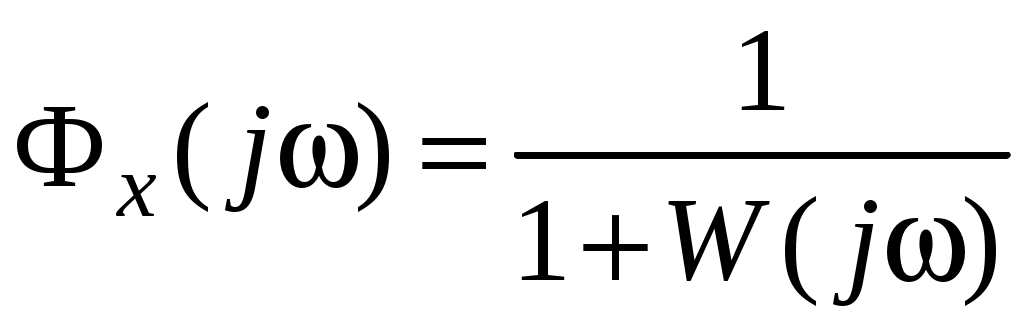– передаточная функция замкнутой системы по ошибке.

СКО будет равно

.

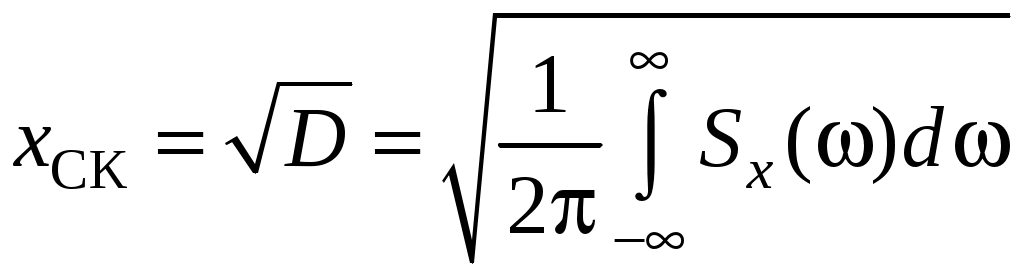2. Имеется помеха f(t), задающее воздействие g(t) = 0. Справедливы соотношения

;

.

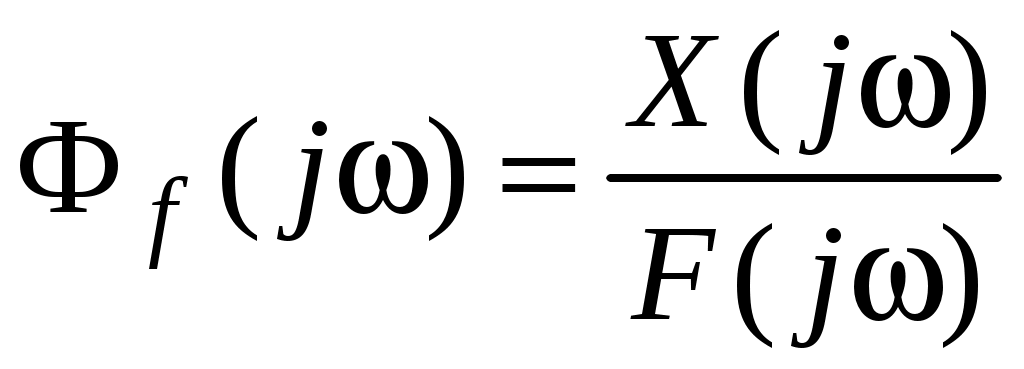Если же помеха действует на входе системы, то расчет СКО аналогичен первому случаю.

3. Имеется и сигнал и помеха.

Общее выражение для спектральной плотности ошибки

,

гдеS_fg() и S_gf() – взаимные спектральные плотности сигнала и помехи; знак «*» показывает сопряженную комплексную величину.

Если корреляции между сигналом и помехой нет, третье и четвертое слагаемые в выражении равны нулю.

Аналогичным образом можно найти и параметры для выходного сигнала

y(t). При этом необходимо использовать частотную передаточную функцию замкнутой системы

12.5. Расчеты по минимуму ошибки

Если на систему одновременно действует полезный сигнал и помеха, то может быть решена задача оптимального расчета системы с тем, чтобы обеспечить наименьшую результирующую ошибку системы.

Критерием является минимальное значение результирующей ошибки системы, определяемой сигналом и помехой. Для случайных процессов обычно ограничиваются оценкой среднеквадратической ошибки. Необходимо обеспечить минимум среднеквадратической ошибки при одновременном действии сигнала и помехи.

Критерий выглядит следующим образом:

.

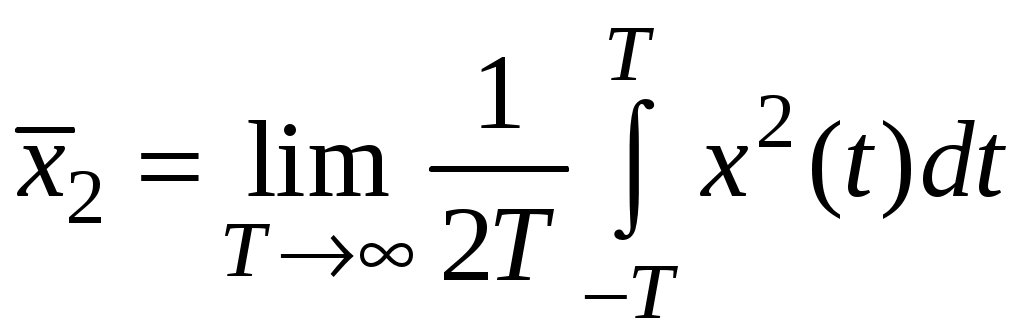Нежелательность ошибки пропорциональна квадрату ее величины.

Возможны две формулировки данной задачи.

1. Имеется САУ заданной структуры. Необходимо так выбрать ее параметры, чтобы обеспечить минимум СКО при заданных статистических параметрах сигнала и ошибки.

Решение ищется следующим образом: зная спектральную плотность ошибки, теоретически находится выражение для расчета дисперсии и СКО. Это выражение зависит от параметров системы, полезного сигнала и помехи. Ищутся условия на параметры системы для обеспечения минимума дисперсии. В простых случаях можно применить известные методы нахождения экстремума функции путем дифференцирования и приравнивания к нулю частных производных.

2. Ставится вопрос о нахождении оптимальной структуры системы и параметров звеньев для получения теоретически минимальной среднеквадратической ошибки при заданных вероятностных характеристиках полезного сигнала и помехи.

Решение следующее: находится теоретическая передаточная функция замкнутой системы, и к ней стремятся при проектировании. Возможна ситуация, что реализация САУ с такой оптимальной передаточной функцией будет сопряжена со значительными трудностями.

13. Нелинейные САУ

Анализ нелинейных САУ (НСАУ) представляет собой достаточно трудную задачу. При ее решении стремятся свести такую САУ к линейной с определенными допущения и ограничениями.

К таким системам относятся те, в которых имеется хотя бы одно звено

, описываемое нелинейными дифференциальными уравнениями.

Нелинейные звенья могут быть следующих видов:

релейного типа;
с кусочно-линейной характеристикой;
с криволинейной характеристикой любого очертания;
имеется произведение и другие комбинации переменных;
нелинейное звено с запаздыванием;
импульсное звено;
логическое;
описываемое кусочно-линейным дифференциальным уравнением.

Нелинейности могут быть статические и динамические. Статические описываются нелинейными статическими характеристиками, а динамические – нелинейными дифференциальными уравнениями.

13.1. Общий метод составления уравнений нелинейных САУ

Сначала выполняется, где возможно, линеаризация звеньев. При этом используются различные методы, например, разложение нелинейной функции в ряд Тейлора в окрестностях некоторой точки. В результате остаются неописанными так называемые существенно нелинейные звенья. Обычно их не более одного-двух. Затем составляют уравнения для этих звеньев со всеми возможными упрощениями их характеристик. Получается система обыкновенных линейных уравнений, к которым добавляется одно-два нелинейных уравнения.

В соответствии с этим, обобщенную структурную схему любой НСАУ при наличии одного нелинейного звена можно представить в виде (рис. 73).

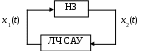
Рис. 73. Обобщенная схема НСАУ с одним нелинейным звеном

Имеется одно нелинейное звено (НЗ) и линейная часть САУ (ЛЧ САУ).

Все НСАУ делятся на два больших класса.

1. Уравнение нелинейного звена имеет любой вид, но под знаком нелинейной функции либо только входная (или ее производные) величина, либо только выходная (или ее производные) величина. Такую систему можно свести к нарисованной выше схеме.

2. Любое число нелинейных звеньев. Под знак нелинейной функции входят обычные переменные, но связанные друг с другом линейной передаточной функцией.

Процессы в НСАУ имеют существенные особенности, поэтому их анализ является сложным. Это касается и устойчивости.

С точки зрения устойчивости система имеет несколько состояний.

1. Устойчивое равновесное состояние с постоянным значением регулируемой величины.

2. Устойчивые автоколебания (собственные колебания с постоянной амплитудой) при отсутствии внешнего воздействия.

3. Область неустойчивости.

4. Области, соответствующие другим, более сложным случаям.

В таких системах можно говорить об устойчивости в «малом» и в «большом».

Система устойчива в «малом», если существуют начальные условия, которые не выводят выходные отклонения за определенную величину. Если же существуют начальные условия, которые выводят выходные отклонения за определенную величину, то система неустойчива в «большом» (рис. 74).

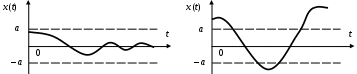
Рис. 74. Устойчивость НСАУ
а) НСАУ устойчива в «малом»; б) НСАУ неустойчива в «большом»

13.2. Фазовое пространство

Для наглядного представления процессов нелинейных САУ вводится понятие «фазовое пространство», которое заключается в следующем.

Дифференциальное уравнение замкнутой системы n-го порядка заменяется системой дифференциальных уравнений первого порядка.

,

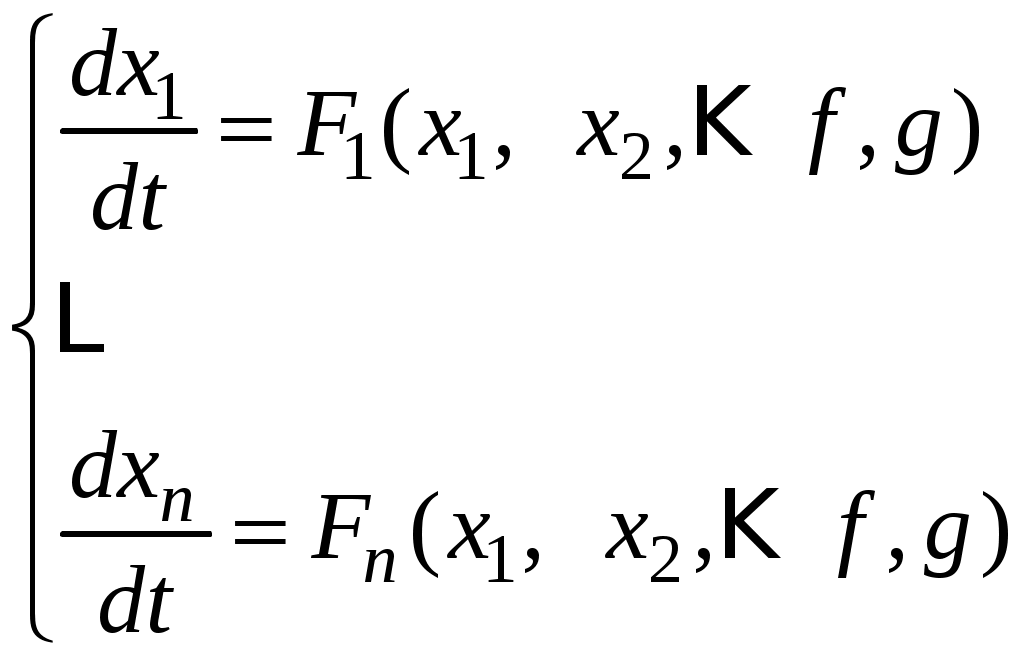где x₁ – выходная величина;

x₂ – x_n – вспомогательные переменные;

f, g – входные воздействия (возмущающее и задающее);

x₁₀ = x₁(t = 0), x₂₀ = x₂(t = 0) … – начальные условия.

Эти дифференциальные уравнения можно представить геометрически в n-мерном пространстве. Например, при n = 3 (рис. 75).

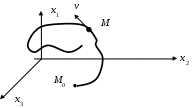
Рис. 75. Трехмерное фазовое пространство

В реальном процессе управления в каждый момент времени величины x₁, x₂, x₃имеют вполне определенные значения. Это соответствует вполне определенному положению точки М в пространстве. Точка М называется изображающей. С течением времени величины x₁, x₂, x₃ изменяются, точка М перемещается по определенной траектории, показывая так называемую фазовую траекторию. Следовательно, траектория движения точки М может служить наглядной геометрической иллюстрацией динамического поведения САУ в процессе управления.

Рассмотрим пример фазовых траекторий некоторых линейных САУ. Пусть они описываются уравнением