Файл: Учебное пособие Рыбинск 2007 удк 681. 5 Павлов Р. В. Основы теории управления. Учебное пособиергата. Рыбинск, 2007. 83 с.doc

.

Корень р₃ найдем из следующих соображений: берем исходное уравнение и приравниваем все коэффициенты при переменных одной степени.

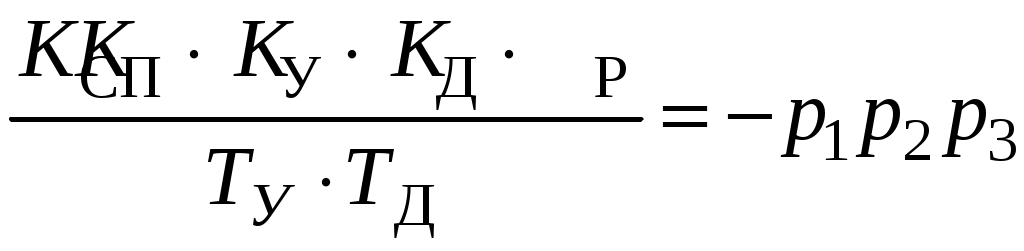, следовательно, р₃ = –8570.

Оптимальный коэффициент усиления тахогенератора находится из следующего соотношения:

.

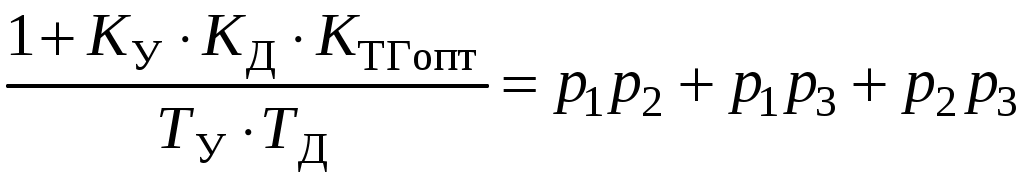Получаем:

.

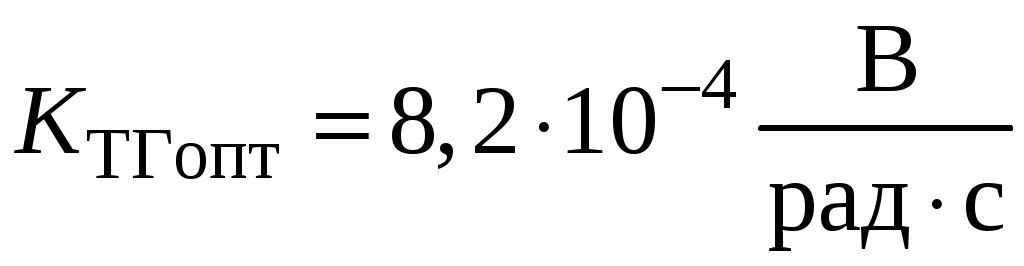Этот коэффициент больше минимального, рассчитанного выше, поэтому требования устойчивости соблюдаются.

---

12. Случайные процессы в САУ

12.1. Основные понятия

Выше были изучены процессы работы САУ при поступлении на ее вход детерминированных сигналов.

Во многих случаях входной сигнал может принимать случайные значения. При этом можно оценивать только вероятностные характеристики.

Пример случайного воздействия: следящая система доплеровского измерителя скорости. Спектральные характеристики процессов САУ в этом случае представлены на рис. 66.

Доплеровская частота  зависит не только от скорости движения объекта, но и от угла падения луча и вида подстилающей поверхности, поэтому носит случайный характер. При этом спектральная характеристика принимаемого сигнала имеет амплитуду S_ и ширину , изменяющуюся случайным образом.



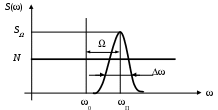
Рис. 66. Спектральные характеристики случайных процессов САУ

_{0 –} излучаемая частота;

_П – принимаемая частота;

 – ширина спектра.

В этой следящей системе имеют место паразитные сигналы (шумы). В простейшем случае шум равномерно распространен по всем частотам.Его спектральная плотность N.

12.2. Характеристики случайных величин и процессов

Кратко остановимся на основных характеристиках случайных величин и процессов.

Случайная величина может быть непрерывной и дискретной.

Случайным процессом называется изменение случайной величины во времени.

Важное значение при описании случайных величин и процессов имеет понятие вероятности. Вероятность – это предельное значение частоты появления события

,

где n – число появлений события в испытаниях;

N – общее число испытаний.

Полное описание случайной величины дает закон распределения вероятности P(х) для дискретной величины и закон распределения плотности вероятности W(х) для непрерывной величины. Соотношение между этими параметрами представлено на рис. 67.

Часто при анализе случайных величин и процессов ограничиваются частными характеристиками. Как правило, это математическое ожидание

---

и дисперсия D.



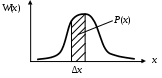
Рис. 67. Плотность вероятности и вероятность для непрерывной величины

Математическое ожидание можно определить как среднее значение, а дисперсию – как средний разброс значений случайной величины относительно ее математического ожидания. Для непрерывной величины справедливы выражения

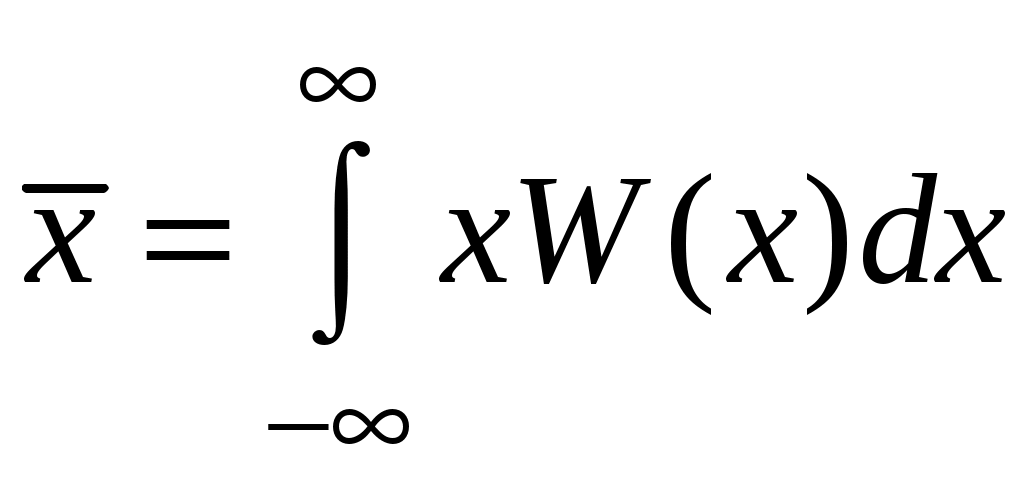– математическое ожидание;

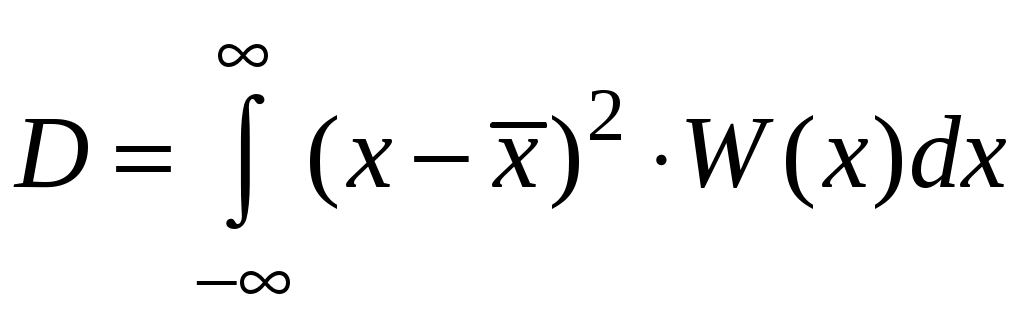– дисперсия.

Важное значение в теории случайных процессов имеет понятие корреляционной функции R. Она показывает степень влияния друг на друга или двух случайных процессов, или различных значений одного случайного процесса. В последнем случае для моментов времени t₁ и t₂ имеем

,

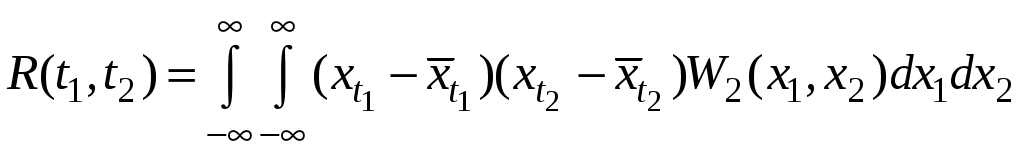где W₂ – это двумерная плотность распределения вероятности для процессов x₁ и x₂.

Существует широкий класс стационарных случайных процессов. У этих процессов постоянные вероятностные параметры.

Поэтому корреляционная функция в данном случае будет зависеть только от расстояния между отсчетами  = t₁ – t₂,. Она обычно обозначается какR().

Свойства корреляционной функции (рис. 68):

1) четная R(–) = R();

2) убывающая;

3) если  = 0, то R() = D(дисперсия).

В теории случайных процессов широко используется понятие спектральной плотности. Существует простая связь между спектральной плотностью и корреляционной функцией через преобразование Фурье:

;

.


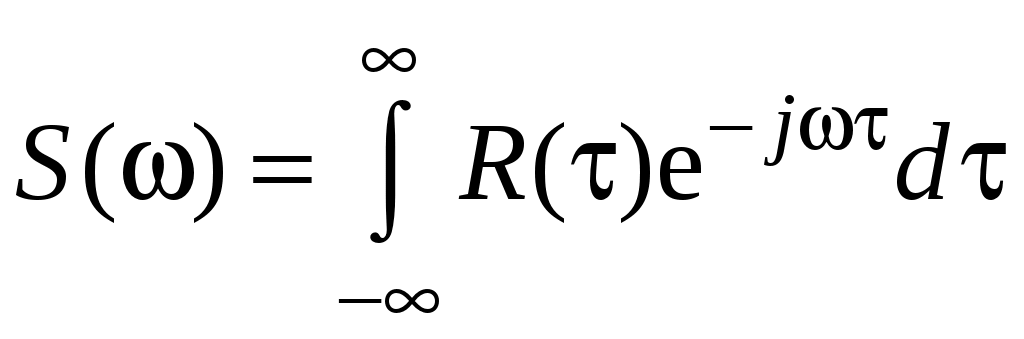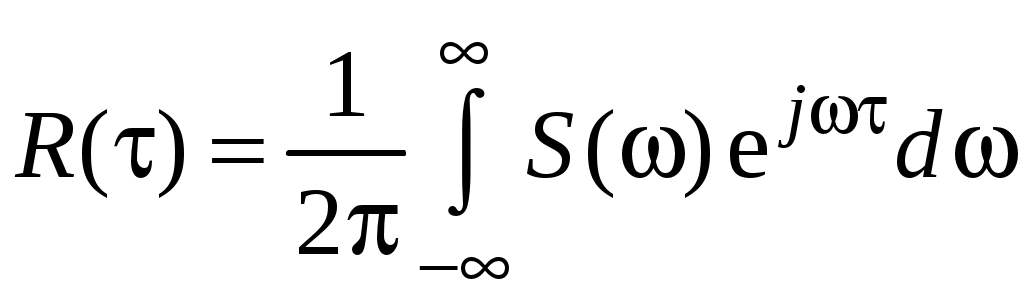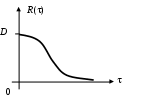
Рис. 68. Корреляционная функция

Если корреляционная функция и спектральная плотность – вещественные четные функции, то

---

;

.

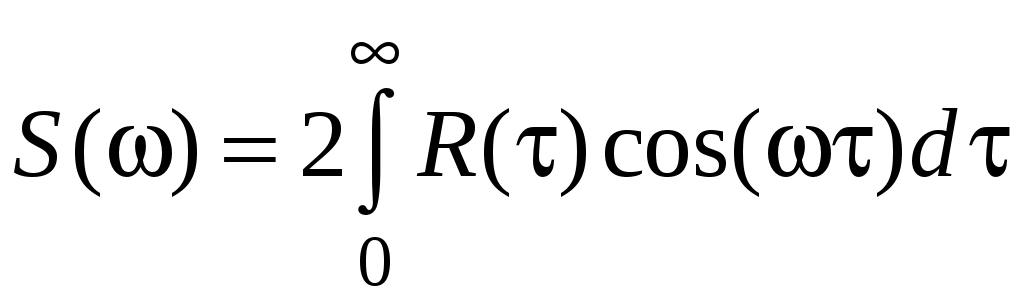
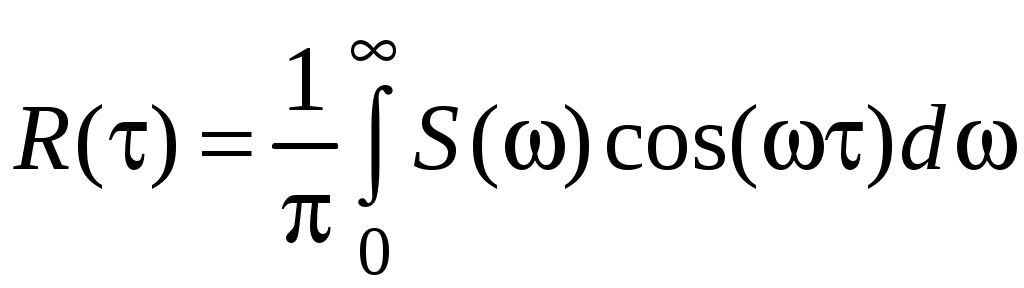Чем шире спектр случайного сигнала (сигнал быстрее изменяется), тем ýже корреляционная функция (слабее влияние соседних значений сигнала друг на друга) и наоборот. Предельное соотношение для сигнала типа шум – соседние значения сигнала не зависят друг от друга.

---

12.3. Прохождение случайного сигнала
через линейную непрерывную систему

Структурная схема САУ имеет вид (рис. 69).


Рис. 69. Структура САУ

Задачу можно сформулировать следующим образом: зная вероятностные характеристики входного сигнала x₁(t) (матожидание и дисперсию D₁), надо определить вероятностные характеристики выходного сигнала x₂(t) (матожидание и дисперсию D₂).

Существует два метода решения этой задачи:

1) расчеты во временной области;

2) расчеты в частотной области.

1. Расчеты во временной области.

Рассмотрим математические соотношения для каждого метода.

Для определения математического ожидания используется формула свертки, в которую вместо значений сигналов нужно подставить значения их математических ожиданий.

,

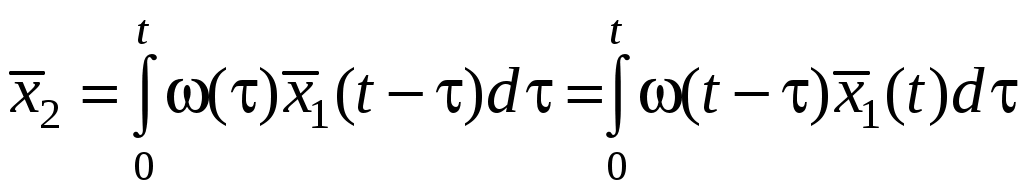где (t) – весовая функция.

Для нахождения дисперсии на выходе предварительно необходимо найти корреляционную функцию. Корреляционная функция на выходе:

,

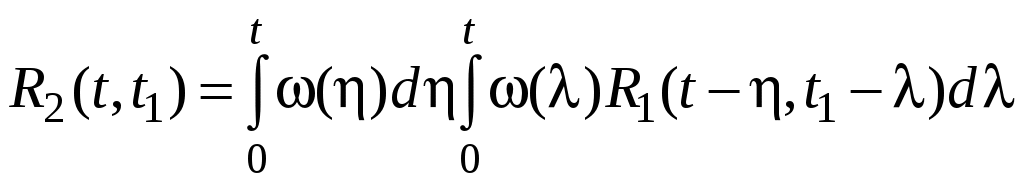где  и  – переменные интегрирования

При подстановке t = t₁ получим выражение для дисперсии.

Если САУ устойчива, то корреляционная функция и дисперсия стремятся к некоторым пределам, определяющим стационарный процесс на выходе.

Рассмотрим пример.

Имеется интегрирующее звено с передаточной функцией 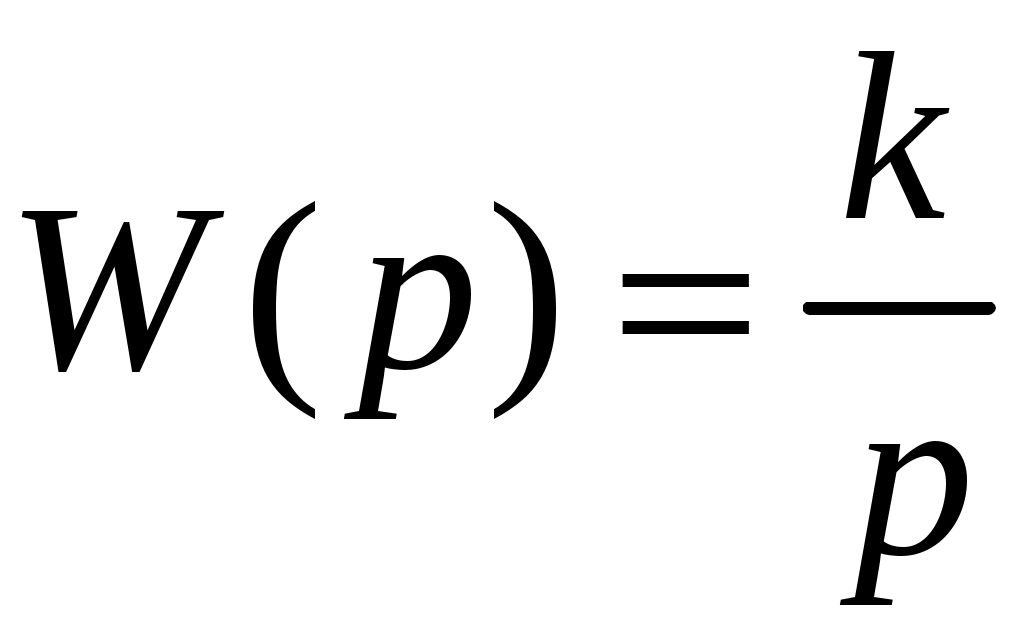и весовой функцией ;

На вход подается белый гауссовский шум (БГШ) с характеристиками (рис. 70).

«Белый» шум означает равномерное распределение спектральной плотности N_Ш во всем диапазоне частот. «Гауссовский» – плотность распределения вероятности имеет нормальный закон. Корреляционная функция шума

---