Файл: Иркутский национальный исследовательский технический университет институт заочновечернего обучения Кафедра Самолётостроения и эксплуатации авиационной техники.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 349
Скачиваний: 3
СОДЕРЖАНИЕ
2 Схематизация нагрузок, действующих на конструкцию крыла в полете
2.1 Построение эквивалентного крыла
2.2 Определение действующих нагрузок
3 Построение эпюр внутренних силовых факторов, действующих в сечениях эквивалентного полукрыла
4 Проектировочный расчет крыла
4.1 Схематизация расчетного сечения
4.2 Проектировочный расчет поясов расчетного сечения
4.2.1 Схематизация действия изгибающего момента
4.2.2 Проектировочный расчет верхнего пояса сечения
4.2.3 Проектировочный расчет полок лонжеронов
4.2.4 Проектировочный расчет нижнего пояса сечения
4.3 Проектировочный расчет стенок лонжеронов
4.4 Определение координат центров тяжести продольных элементов в сечении кессона
5 Проверочный расчет крыла на изгиб методом редукционных коэффициентов или методом В. Н. Беляева
5.1 Краткое описание методики выполнения проверочного расчета
7 Проверочный расчет крыла на сдвиг и кручение
6. Анализ результатов
 -го приближения.
-го приближения.В верхней полке главного (первого) лонжерона напряжения меньше разрушающих:
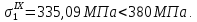
В нижней полке главного лонжерона напряжения так же меньше разрушающих:
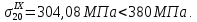
Напряжения в полках главного лонжерона не превышают разрушающие. Следовательно, можно выполнять десятое приближение.
5.11 Десятое приближение
-
Требуется определить редукционные коэффициенты девятого приближения,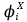 , для всех продольных ребер.
, для всех продольных ребер.
Для всех продольных элементов редукционные коэффициенты остаются равными редукционным коэффициентам девятого приближения, поскольку значения расчётных напряжений меньше или равны предельным. Полученные результаты редукционных коэффициентов приведены в таблице 5.10.
-
В десятом приближении определяется смещение центральной оси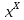 сечения относительно центральной оси девятого приближения. Поскольку ординаты продольных элементов
сечения относительно центральной оси девятого приближения. Поскольку ординаты продольных элементов  , приведенные в таблице 4.2, определены относительно хорды, то по соответствующей формуле смещение определится как:
, приведенные в таблице 4.2, определены относительно хорды, то по соответствующей формуле смещение определится как:
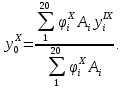
-
Определение ординат продольных ребер относительно центральной оси,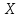 -го приближения:
-го приближения:
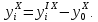
4. Вычисление осевого момента инерции сечения,
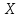 -го приближения:
-го приближения: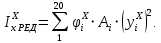
5. Вычисление напряжений в продольных ребрах,
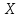 -го приближения:
-го приближения: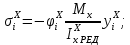
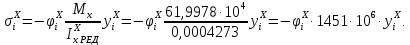
Все результаты вычислений для десятого приближения представлены в таблице 5.10.
Таблица 5.10 – Десятое приближение
 | 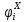 | 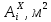 |  | 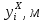 | 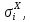  |  | 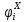 | 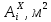 | 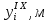 | 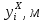 | 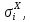  |
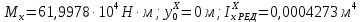 | |||||||||||
| 1 | 1 | 0,00139 | 0,2309 | 0,2309 | -335,09 | 20 | 1 | 0,001349 | -0,2096 | -0,2096 | 304,08 |
| 2 | 0,9456 | 0,000273 | 0,2550 | 0,2550 | -349,94 | 19 | 1 | 0,000255 | -0,2222 | -0,2222 | 322,36 |
| 3 | 0,9169 | 0,000273 | 0,2630 | 0,2630 | -349,94 | 18 | 1 | 0,000255 | -0,2262 | -0,2262 | 328,17 |
| 4 | 0,9169 | 0,000273 | 0,2630 | 0,2630 | -349,94 | 17 | 1 | 0,000255 | -0,2292 | -0,2292 | 332,52 |
| 5 | 0,9419 | 0,000273 | 0,2560 | 0,2560 | -349,94 | 16 | 1 | 0,000255 | -0,2302 | -0,2302 | 333,97 |
| 6 | 0,9964 | 0,000273 | 0,2420 | 0,2420 | -349,94 | 15 | 1 | 0,000255 | -0,2302 | -0,2302 | 333,97 |
| 7 | 1 | 0,000273 | 0,2230 | 0,2230 | -323,63 | 14 | 1 | 0,000255 | -0,2282 | -0,2282 | 331,07 |
| 8 | 1 | 0,000273 | 0,1990 | 0,1990 | -288,80 | 13 | 1 | 0,000255 | -0,2252 | -0,2252 | 326,72 |
| 9 | 1 | 0,000273 | 0,1730 | 0,1730 | -251,08 | 12 | 1 | 0,000255 | -0,2202 | -0,2202 | 319,46 |
| 10 | 1 | 0,001178 | 0,1421 | 0,1421 | -206,24 | 11 | 1 | 0,001133 | -0,2073 | -0,2073 | 300,74 |
6. Анализ результатов
 -го приближения.
-го приближения.В верхней полке главного (первого) лонжерона напряжения меньше разрушающих:
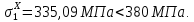
В нижней полке главного лонжерона напряжения так же меньше разрушающих:
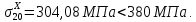
Напряжения в полках главного лонжерона не превышают разрушающие. Следовательно, можно выполнять девятое приближение.
Имеет место некоторый процент недонапряжения, особенно заметно недонагружение верхнего пояса заднего лонжерона.
Стрингеры с номерами 2…6 верхнего пояса редуцированы. Начиная со второго приближения все остальные продольные элементы сечения крыла стабильно недонапряжены. Поэтому значения их редукционных коэффициентов остаются неизменными. Расчёт останавливается после того, как стабилизировались значения всех характеристик сечения крыла: положение центра тяжести сечения; значение осевого момента инерции сечения; значения напряжений.
Не смотря на стабильность значений параметров, конструкция перетяжелена. При проектировании реальной конструкции следовало бы выполнить расчёты, направленные на повышение действующих напряжений вплоть до предельных. В частности, возможно снижении массы конструкции за счет уменьшение толщины обшивки нижнего пояса сечения.
7 Проверочный расчет крыла на сдвиг и кручение
Для проведения проверочного расчета крыла на сдвиг и кручения требуется определить нагрузки действующие в каждой панели обшивки в расчетном сечении крыла.
Поток касательных усилий, действующих в панелях обшивки замкнутого контура, можно определить, решив уравнение:
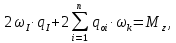
где
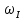 – площадь замкнутого контура до расчетной панели обшивки;
– площадь замкнутого контура до расчетной панели обшивки;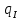 – усилие, действующее в замыкающей панели обшивки;
– усилие, действующее в замыкающей панели обшивки;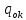 – усилие, действующее в k -той панели обшивки;
– усилие, действующее в k -той панели обшивки;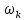 – площадь замкнутого контура до расчетной панели обшивки;
– площадь замкнутого контура до расчетной панели обшивки; – крутящий момент в расчетном сечении.
– крутящий момент в расчетном сечении.Площадь замкнутого контура для панелей определяется измерением на профиле крыла в расчетном сечении построенном в масштабе 1:1 в системе автоматизированного проектирования AutoCAD с помощью встроенных программных средств. Методика измерения площади показана на рисунке 7.1, а для замыкающей панели контура и на рисунке 7.1, б для k-той панели контура. Результаты измерений приведены в таблице 7.1.
а – измерение площади замкнутого контура для замыкающей панели;
б – измерение площади замкнутого контура для k-той панели
Рисунок 7.1 – Методика определения площадей
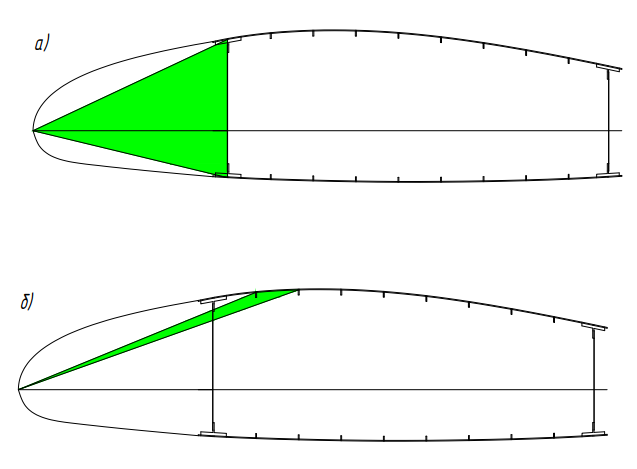
Усилие, действующее в k-той панели обшивки определяется по формуле:
где
 – поперечная сила, действующая в расчетном сечении;
– поперечная сила, действующая в расчетном сечении; – изгибающий момент, действующий в расчетном сечении;
– изгибающий момент, действующий в расчетном сечении;
– угол конусности крыла;
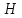 – максимальная высота профиля в рассматриваемого профиля;
– максимальная высота профиля в рассматриваемого профиля;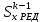 – статический момент для ребра, предшествующего k-той панели;
– статический момент для ребра, предшествующего k-той панели;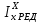 – осевой момент инерции сечения;
– осевой момент инерции сечения;В свою очередь статический момент определяется по формуле:
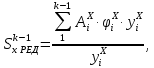
где
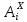 – площадь продольного ребра в последнем приближении;
– площадь продольного ребра в последнем приближении; – редукционный коэффициент последнего приближения;
– редукционный коэффициент последнего приближения;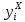 – ордината продольного ребра в последнем приближении;
– ордината продольного ребра в последнем приближении;Для определения угла конусности воспользуемся соотношением:
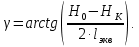
Так как величины
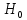 и
и 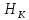 неизвестны, но при расчете крыла принято допущение о том, что профиль является постоянным по всей длине сечения можно записать, что:
неизвестны, но при расчете крыла принято допущение о том, что профиль является постоянным по всей длине сечения можно записать, что: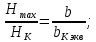
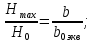
откуда:
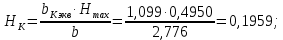
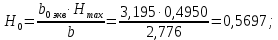
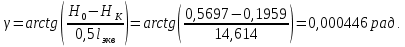
Значения
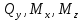 определены ранее в разделе 3 данной курсовой работы и для расчетного сечения составляют:
определены ранее в разделе 3 данной курсовой работы и для расчетного сечения составляют: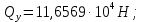
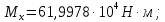
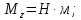
Результаты вычислений усилий в панелях обшивки удобно представить в виде таблицы 7.2.
Таблица 7.2 – Вычисление усилий в панелях контура
 | 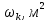 | 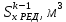 | 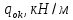 | 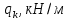 |  | 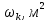 | 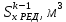 | 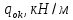 | 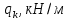 |
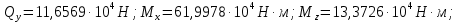 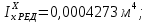 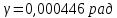 | |||||||||
| 2 | 0,014889 | 0,0003868 | 30,315205 | 1,983914 | | | | | |
| 3 | 0,019103 | 0,0004526 | 32,938997 | 4,607705 | 20 | 0,008567 | 0,0003491 | 58,304627 | 29,97333 |
| 4 | 0,022941 | 0,0005184 | 35,5628 | 7,231508 | 19 | 0,009395 | 0,0002831 | 60,400199 | 32,06891 |
| 5 | 0,026821 | 0,0005843 | 38,186603 | 9,855312 | 18 | 0,009979 | 0,0003398 | 62,359373 | 34,02808 |
| 6 | 0,030725 | 0,0006501 | 40,810568 | 12,47928 | 17 | 0,010754 | 0,0003974 | 64,181116 | 35,84982 |
| 7 | 0,034280 | 0,0007110 | 43,434528 | 15,10324 | 16 | 0,011818 | 0,0004559 | 65,842694 | 37,5114 |
| 8 | 0,037287 | 0,0007653 | 46,05832 | 17,72703 | 15 | 0,012819 | 0,0005146 | 77,200138 | 48,86885 |
| 9 | 0,039776 | 0,0008125 | 48,682353 | 20,35106 | 14 | 0,013777 | 0,0005733 | 58,324572 | 29,99328 |
| 10 | 0,038305 | 0,0009799 | 51,237753 | 22,90646 | 13 | 0,015283 | 0,0006315 | 55,751828 | 27,42054 |
| 11 | 0,344439 | 0,0007451 | 53,700154 | 25,36886 | 12 | 0,013570 | 0,0006889 | 53,134845 | 24,80355 |